Использование блоков сжатия и возбуждения для повышения точности автоматической классификации остеоартрита коленного сустава при помощи сверточных нейронных сетей

Одной из самых распространенных болезней опорно-двигательного аппарата считается остеоартрит (ОА). Основным симптомом этой болезни является износ и разрушение межсуставного хряща, что приводит к ограничению функциональности сустава и возникновению болей при движении. На текущем этапе развития медицины не существует эффективных способов лечения данной болезни, кроме полной замены сустава на искусственный аналог после его полного разрушения. При этом остеоартрит является стадийной болезнью [1], и при раннем обнаружении есть возможность замедлить процесс разрушения сустава.

Самым распространенным и дешевым неинвазивным способом диагностики остеоартрита на данный момент является использование рентгеновского излучения. Ввиду того, что хрящи на рентгенограммах не видны, оценку степени развития остеоартрита осуществляют по косвенным признакам – сужению межсуставной щели, деформации формы кости и появления на костях определенного вида наростов, называемых остеофитами.

Существуют различные шкалы оценки прогрессирования остеоартрита, при этом одной из самых рас-

пространенных является шкала Келлгрена–Лоуренса. К недостаткам этой шкалы относят ее субъективность, т.е. результат оценки рентгенограммы сильно зависит от опыта эксперта, который выполняет эту оценку. Использование автоматических методов анализа рентгенограмм для классификации остеоартрита позволило бы существенно снизить субъективность диагноза и сделать его более надежным.

Для автоматической диагностики остеоартрита могут быть использованы разнообразные методы – начиная с автоматизации стандартных измерений, проводимых экспертом (расстояния между костями сустава и т.п.) и заканчивая автоматическим анализом графического содержимого рентгенограмм. При этом самыми популярными в данный момент (а также показывающими самое высокое качество классификации) являются методы, основанные на использовании глубокого обучения и сверточных нейронных сетей в частности.

Целью данной работы является исследование возможности повышения точности работы стандартных архитектур сверточных нейронных сетей, которые показали наилучшие результаты в предыдущих работах по автоматической классификации остеоартрита, путем их модификации при помощи добавления блоков сжатия и возбуждения [14].

1.    Оценка прогрессирования остеоартрита по шкале Келлгрена–Лоуренса

В настоящее время существуют различные подходы к оценке развития остеоартрита – в отечественном пространстве ранее применялась классификация Н.С. Косинской [2], в Европе и Северной Америке преобладает шкала Келлгрена–Лоуренса [3], а в некоторых случаях используется атлас международного общества изучения остеоартрита (OARSI [4]).

Ввиду того, что большинство размеченных данных для экспериментов по автоматической классификации остеоартрита опираются на шкалу Келлгрена– Лоуренса, а также для удобства сравнения с другими работами, в данном исследовании в качестве базовой шкалы была выбрана именно она. Эта шкала состоит из 5 стадий развития остеоартрита (стадия 0 – отсутствие признаков остеоартрита):

• •    none: патологии отсутствуют;

• •    сомнительные рентгенологические признаки (doubtful): сужения суставной щели нет или есть небольшое сужение, заострения на краях суставной поверхности (рис. 1а);

• •    минимальные изменения (minimal): небольшое сужение суставной щели, небольшие единичные остеофиты на краях суставной поверхности (рис. 1б);

• •    умеренные проявления (moderate): умеренное сужение суставной щели, множественные остеофиты на краях суставной поверхности, небольшие деформации суставной поверхности (рис. 1в);

• •    выраженные изменения (severe): суставная щель почти не прослеживается, грубые остеофиты на краях суставной поверхности, деформация эпифизов костей, образующих сустав (рис. 1г).

2.    Обзор существующих методов автоматической диагностики остеоартрита

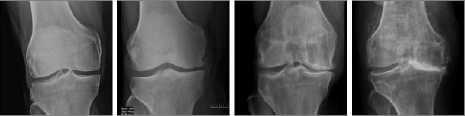
a)                б)                в)                г)

Рис. 1. Пример изображений коленного сустава с разными стадиями остеоартрита по шкале Келлгрена–Лоуренса

Наличие остеоартрита диагностируется на стадии 2 и выше [5], поэтому в некоторых исследованиях нулевую и первую стадии объединяют в одну (отсутствие патологий). Как будет показано дальше, объединение 0-й и 1-й стадий также позволяет повысить точность классификации, т.к. основные ошибки классификации как раз происходят между стадиями 0 и 1 из-за слишком незначительных отличий между ними.

За годы исследований в области автоматической диагностики стадий остеоартрита были предложены различные подходы к решению данной задачи.

В [19] классификация ОА осуществляется при помощи модификации алгоритма ближайших соседей, в качестве данных для которого выступают различные характеристики изображения вроде первых четырех моментов, текстурных и статистических характеристик и др. В работе используется датасет из 350 изображений, которые разделяются на тренировочную и тестовую выборки в соотношении 7:3, а в качестве шкалы классификации – шкала Келлгрена–Лоуренса с отброшенной последней стадией (стадия severe ). Среднеклассовая точность (количество верно классифицированных изображений) в данном случае не превышает 47%.

В работе [8] для решения задачи автоматической классификации рассматриваются деревья решений, байесовский классификатор и логистическая регрессия по различным текстурным характеристикам – признакам Харалика, разного рода гистограммам и т.п. При этом для экспериментов был использован да-тасет из 130 рентгенограмм.

Одной из первых работ, в которой было предложено применять для автоматической классификации сверточные нейронные сети, можно считать работу [9]. При использовании простой, обученной с нуля сверточной сети, состоящей из 5 сверточных и одного полносвязного слоя, удалось достичь точности классификации около 60%. В работе [15] приводится исследование применимости к классификации остеоартрита стандартных архитектур сверточных сетей, предтренированных на ImageNet и дообученных на датасете OAI.

В работе [10] изучаются глубокие сиамские сети, которые используют симметрию на изображении и состоят из двух ветвей, каждая из которых независимо от другой работает со своей частью коленного сустава. При этом достигается точность классификации в 67,49%. В [11] представлена модель, обученная не только классификации остеоартрита, но также измерению сужения межсуставной щели и определению наличия остеофитов. Подход основан на использовании комбинации двух сетей, каждая из которых действует независимо от другой и состоит из двух частей – предтренированных на ImageNet сверточных и 7 полносвязных слоев. Для связи между сверточными и полносвязными слоями используется усредняющий пуллинг. Полученная точность на задаче классификации остеоартрита – 66,68 %.

Оригинальная идея представлена в работе [20], где, помимо рентгенограмм коленного сустава, предлагается использовать некоторые характеристики походки пациента (частота шагов, ширина шага, угол сгибания колена, угол разгибания бедра и др.). Дата-сет состоит из 728 рентгенограмм коленей 364 пациентов с прикрепленной информацией о походке. В качестве метода классификации используется классификатор SVM, который опирается на особенности походки и карту признаков рентгенограммы, извле- ченную при помощи нейронной сети с архитектурой Inception-ResNet-v2. Полученная среднеклассовая точность классификации – 64,7 % без применения метаданных и 75,2 % при использовании информации о походке на тестовой выборке из 218 изображений.

Помимо экспериментов с различными архитектурами, существуют исследования различных способов обучения, которые направлены на уменьшение ошибки между классами при помощи функции потерь специального вида. В [12] это достигается при помощи функции потерь, которая назначает штраф в зависимости от «расстояния» между реальной и предсказанной степенями остеоартрита (чем сильнее отличается класс, тем больше штраф). Исследуются несколько стандартных архитектур, таких как ResNet, VGG и др., при этом наибольшая точность 69,7% достигается на предтренированной VGG-19 при использовании во время обучения предложенной функции потерь.

В [7] проводится исследование сетей с архитектурой DenseNet различной глубины и с различными функциями потерь. Показано, что наилучшая среднеклассовая точность 68,98 % была достигнута для случая предтренированной сверточной сети архитектуры DenseNet-121 при использовании в качестве функции потерь классической кросс-энтропии. Ансамблю из нескольких таких моделей, обученных при задании разных случайных начальных значений для генератора случайных чисел, удалось достигнуть точности 71,08 %. Исследования архитектуры DenseNet для задачи классификации остеоартрита также приводятся в [13], однако в этом случае применяется не пятиклассовая шкала Келлгрена–Лоуренса, а шкала с объединенными 0-м и 1-м классами. В этом случае авторами была получена среднеклассовая точность 77,2 % при использовании ансамбля из трех моделей.

В нашем исследовании мы рассматриваем использование блоков сжатия и возбуждения [14] для повышения точности классификации остеоартрита как для полной, так и для сокращенной шкалы Келлгрена– Лоуренса применительно к архитектурам, которые в предыдущих работах показали наилучшие результаты – к архитектурам ResNet [21] и DenseNet [22] различной глубины.

3.    Данные

3000 рентгенограмм различных частей тела (боковой и фронтальной проекций коленей, бедер, рентгенограмм кистей рук и др.). Для каждого обследования, помимо набора рентгенограмм различных частей тела, присутствуют описания экспертов, включая степень ОА по шкале Келлгрена–Лоуренса, оценку сужения межсуставной щели, наличие остеофитов и т.п.

Несмотря на кажущееся обилие данных, в ходе проведения экспериментов было обнаружено, что да-тасет CHECK содержит большое количество ошибок в разметке, а доступ к датасету MOST ограничен из-за прекращения финансирования и реорганизации, поэтому в качестве основных данных для их проведения был выбран набор данных The Osteoarthritis Initiative (OAI).

Как было упомянуто ранее, данный набор содержит информацию о 4796 пациентах в возрасте от 45 до 79 лет, наблюдаемых в течение 14 лет. Помимо рентгенограмм коленного сустава, в датасете также содержится информация о различных измерениях, наличии остеофитов, сужении межсуставного пространства, стадиях остеоартрита, полученных от нескольких независимых экспертов и т.п.

Несмотря на то, что в некоторых исследованиях при построении классификаторов остеоартрита, помимо рентгенограмм, используется дополнительная информация в виде разного рода антропометрических данных, клинической истории и т.п. [6], в нашем исследовании классификация остеоартрита выполняется исключительно по рентгенограммам коленного сустава, полученным в двусторонней задне-передней проекции с фиксированным сгибанием сустава (рис. 2).

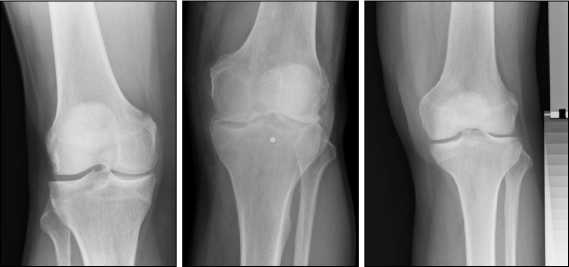
Рис. 2. Пример изображений двусторонней задне-передней проекции с фиксированным сгибанием

Ввиду того, что в наборе данных отсутствует информация о позиционировании на рентгенограмме области сустава, для локализации этой области использовался готовый модуль локализации, также основанный на базе сверточной нейронной сети, описание которого можно найти в [7].

После фильтрации имеющегося набора рентгенограмм и удаления из него низкокачественных изображений (сильно размытых, расфокусированных и т.п.) был получен датасет из 4130 рентгенограмм, в котором содержится 8260 изображений областей коленного сустава.

Данный набор был случайным образом разделен на тренировочную, валидационную и тестовую вы- борки в пропорции 7 : 1 : 2. Распределение изображений областей коленного сустава по степени прогрессирования на них остеоартрита (по шкале Келлгрена– Лоуренса) приведено в табл. 1.

Как можно заметить, полученный датасет является сильно несбалансированным, поэтому для увеличения разнообразия использовалась аугментация данных. Для этого применялись такие преобразования исходных данных, как зеркальное отображение по горизонтали, случайное масштабирование и вращение (на небольшой угол), а также изменение яркости и насыщенности содержимого изображений. После всех преобразований изображение масштабировалось до размера 224 × 224. Все этапы аугментации выполнялись в случайном порядке «на лету», в процессе тренировки моделей.

Табл. 1. Распределение рентгенограмм по шкале

Келлгрена–Лоуренса для тренировочной, валидационной и тестовой выборок: числа в таблице означают количество изображений коленного сустава для каждой категории

Группа	КЛ-0	КЛ-1	КЛ-2	КЛ-3	КЛ-4	Всего
Тренир.	2295	1051	1504	752	175	6604
Валид.	319	148	223	111	25	826
Тестовая	639	296	447	223	51	1656

4.    Описание блоков сжатия и возбуждения

Традиционным центральным блоком сверточной нейронной сети является оператор свертки, который позволяет формировать информативные карты признаков, учитывающие как пространственную, так и межканальную информацию.

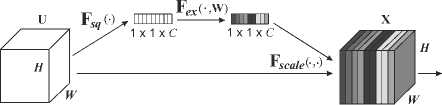
В работе [14] делается акцент на отношениях между разными каналами одного слоя. Авторы предлагают новый элемент архитектуры, называемый блоком сжатия и возбуждения (Squeeze-and-Excitation block, SE), который позволяет усилить обобщающую способность нейронной сети или ее части путем явного моделирования взаимозависимости между различными слоями сверточного блока. Предложенный механизм позволяет выполнять рекалибровку выходных данных сверточного блока (иначе говоря – ставить в соответствие каждому слою его вес), обучаясь использовать глобальную информацию для акцентирования внимания сети на информативных признаках, в то же время подавляя признаки неинформативные. Структура блока сжатия и возбуждения представлена на рис. 3.

CC

Рис. 3. Иллюстрация блока сжатия и возбуждения из работы [14]

Сначала для карты признаков U выполняется операция сжатия Fsq, которая позволяет получить де- скрипторы каждого канала путем агрегирования содержимого каждого слоя в одно число при помощи операции глобального усредняющего пуллинга:

1 HW zc = Fs? (uc ) = „ ZZ uc (i, j)’ (1) H X M i=1 j=1

где z _c - дескриптор канала c ( z e R^C), u_c - содержимое слоя для канала c (изображение размера H × W ).

Для полученного таким образом вектора дескрипторов выполняется процедура адаптивной рекалибровки, или возбуждения ( F scale ). Этот механизм принимает на вход вектор дескрипторов z c и состоит из двух полносвязных слоев, первый из которых обладает нелинейностью в виде ReLU, а второй – нелинейностью в виде сигмоиды. При этом первый полносвязный слой уменьшает размерность вектора на некоторый коэффициент r , а второй слой восстанавливает размерность до исходной. Если обозначить сигмоиду через σ, а нелинейность ReLU через δ, то операцию возбуждения можно выразить следующим образом:

s = F , ( z , W ) = c ( W ₂ 5 ( W i z )), (2)

где W i e R^C/rxC, W ₂ e R^CxC/r - полносвязные слои SE-блока.

В качестве функции активации для второго полносвязного слоя блока используется сигмоида, как показавшая наилучшую эффективность для операции возбуждения [14]. Изменение размерностей на коэффициент r необходимо для того, чтобы обеспечить обучение блока нелинейным зависимостям между каналами, при этом r позволяет гибко управлять сложностью и обобщающей способностью всего SE-блока. В работе показано, что увеличение сложности блока не является прямо пропорциональным улучшению производительности блока, однако маленькие значения r сильно увеличивают количество обучаемых параметров сети. В качестве базового значения коэффициента уменьшения авторами предложено использовать число 16, что является балансом между сложностью блока и его производительностью, однако утверждается, что в некоторых ситуациях для разных уровней нейронной сети, вероятно, потребуется использовать различные значения коэффициента уменьшения r .

Финальный выходной набор данных блока x получается после выполнения рекалибровки карты признаков U с учетом вектора коэффициентов s :

x c = F scak ⁽ u c , s c ) = u c s c , ⁽³⁾

где при помощи F scale ( u c , s c ) обозначено поэлементное перемножение карты признаков u c и соответствующего ей скалярного коэффициента s c .

Из-за своей простой структуры и легковесности SE-блоки могут быть использованы для улучшения уже известных предобученных нейронных сетей, позволяя улучшить итоговую точность их вычислений путем простого добавления соответствующих блоков в уже готовые архитектуры (в том числе и для случая переноса обучения), не приводя при этом к существенному повышению вычислительной сложности моделей.

5.    Структура используемых моделей и особенности реализации

В работе исследовалось влияние SE-блоков на качество работы архитектур ResNet с глубиной 18, 34 и 50 слоев и DenseNet [22] глубиной 121 слой на задаче классификации ОА.

ResNet. Для случая ResNet использовалась схема, предложенная в оригинальной работе [14] – расположение блоков сжатия и возбуждения между финальным сверточным слоем блока и соединением быстрого доступа (рис. 4, слева).

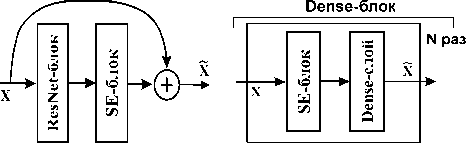
Рис. 4. Схема расположения SE-блоков для архитектур ResNet (слева) и DenseNet (справа)

Обозначим базовый и расширенный строительные блоки ResNet через ResA и ResB соответственно:

ResA( C ) =

3 X 3 X C

3 x 3 x C ,ResB( C 1 , C 2 ) =

SE ( 16, C )

1 X 1 X C 1

3 x 3 x C 1 1 X 1 X C 2

SE ( 16, C ₂)

где C – количество выходных слоев в базовом блоке ResNet, C 2 – количество слоев на выходе из расширенного блока, а SE (16, X) – блок сжатия и возбуждения с коэффициентом редукции r = 16 и количеством входных / выходных слоев, равным X. Каждый сверточный слой сопровождается нормализацией батчей, а первый слой базового блока и первые два слоя для расширенного блока – еще и нелинейностью в виде ReLU. Структура моделей SE-ResNet для разной глубины сетей, принимающих на вход изображение размером 224 × 224, описана в табл. 2.

Здесь conv обозначает сверточный слой с нормализацией батчей, max pool – слой пуллинга, average pool – глобальный усредняющий пуллинг, а fc – полносвязный слой соответствующей размерности. Оригинальные версии ResNet выглядят аналогично за исключением отсутствия SE-блоков в базовом и расширенном строительных блоках.

DenseNet. DenseNet состоит из серии плотносвязанных и транзитных блоков, где назначение вторых – изменение пространственной и канальной размерности данных для соблюдения баланса между обобщающей способностью сети и ее вычислительной сложностью. При этом плотно -связанный блок состоит из т.н. плотных слоев, каждый из которых состоит из свертки 1 × 1 × 128 и свертки 3 × 3 × 32.

Табл. 2. Структура сетей архитектуры ResNet различной глубины с SE-блоками, которые были использованы в исследовании, для случая 5 классов

Выход	SE-ResNet-18 SE-ResNet-34 SE-ResNet-50
112×112	7×7 conv, 64, stride 2
56×56	3 ×3 max pool, stride 2
	ResA (64) ×2 ResA (64) ×3 ResB (64, 256) ×3
28×28	3 ×3 max pool, stride 2
	ResA (128) ×2 ResA (128) ×4 ResB (128, 512) ×4
14×14	3 ×3 max pool, stride 2
	ResA (256) ×2 ResA (256) ×6 ResB (256, 1024) ×6
7×7	3×3 max pool, stride 2
	ResA (512) ×2 ResA (512) ×3 ResB (512, 2048) ×3
1×1	7×7 average pool, 5-d fc, softmax

Блоки сжатия и возбуждения при модификации архитектуры DenseNet для удобства реализации были размещены перед каждым dense-слоем в плотносвязанном блоке (рис. 4, справа), и тогда мы можем обозначить такой слой следующим образом:

DenseLayer i (S ) =

SE(16, S + 32 • i ) 1 x 1 x 128 3 x 3 x 32

где i – номер слоя в плотно -связанном блоке, S – начальное количество слоев в таком блоке (задается для каждого блока), а каждая свертка сопровождается нормализацией батчей и нелинейностью в виде ReLU. В базовом варианте DenseNet SE-блоки в плотных слоях и транзитных блоках отсутствуют. Каждый плотный слой принимает на вход выходные данные всех предыдущих подобных слоев, а на выходе последнего сверточного слоя предоставляет карту признаков с фиксированной глубиной 32, которая конкатенируется с входными данными. Подобная схема на выходе плотно -связанного блока дает набор карт признаков с общим количеством каналов, равным S + 32*N , где N – количество плотных слоев. Структура плотных слоев также фиксирована и отличается лишь количеством каналов во входных данных.

Более подробное описание структуры SE-DenseNet-121 для 5 классов представлено в табл. 3. Для случая 4 классов в структуре сети меняется лишь последний полносвязный слой.

6.    Автоматическая классификация остеоартрита

Основная задача по автоматической классификации остеоартрита в данной работе решается при помощи сверточных сетей с архитектурами ResNet и DenseNet.

В качестве объектов исследования рассматриваются модели, которые показали наилучшие результаты в предыдущих исследованиях – ResNet с глубиной

18, 34 и 50 слоев и DenseNet с глубиной 121 слой, предтренированные на датасете ImageNet, состоящем из изображений 1000 различных классов.

Табл. 3. Структура сети архитектуры DenseNet-121 с SE-блоками, которая была использована в исследовании (SE-DenseNet-121), для случая 5 классов

Тип	Выход	DenseNet-121-18
	112 × 112	7 × 7 conv, 64, stride 2
	56 × 56	3 × 3 max pool, stride 2
SE-блок	56 × 56	SE (4, 64)
Dense-блок (1)	56 × 56	SE (4, 64)
		DenseLayer (64) × 6, i = 1..6
Transition (1)	56 × 56	SE (16, 256)
		1 × 1 conv, 128, stride 2
	28 × 28	3 × 2 max pool, stride 2
Dense-блок (2)	28 × 28	SE (8, 128)
		DenseLayer (128) × 12, i = 1..12
Transition (2)	28 × 28	SE (32, 512)
		1 × 1 conv, 256, stride 2
	14 × 14	3 × 2 max pool, stride 2
Dense-блок (3)	14×14	SE (16, 256)
		DenseLayer (256) × 24, i = 1..24
Transition (3)	14 × 14	SE (64, 1024)
		1 × 1 conv, 512, stride 2
	7 × 7	3 × 2 max pool, stride 2
Dense-блок (4)	7 × 7	SE (32, 512)
		DenseLayer (512) × 16, i = 1..16
	1 × 1	7 × 7 average pool, 5-d fc, softmax

Применяется стандартный для случая переноса обучения подход – замена верхнего полносвязного слоя с количеством выходов, равным 1000, на полносвязный слой с количеством выходов, равным числу классов остеоартрита. После замены производится дообучение модели на новом наборе изображений (в данном случае на датасете OAI), при этом в качестве начальных весов сверточных слоев используются веса, полученные при обучении на ImageNet, что позволяет более эффективно использовать обобщающие способности нейросетевых моделей, чем если бы обучение на новых данных выполнялось с нуля.

В качестве целевой шкалы классификации остеоартрита в исследовании используется как стандартная шкала Келлгрена–Лоуренса, состоящая из 5 классов, так и шкала, в которой нулевой и первый классы объединены в один класс, означающий отсутствие заболевания.

Процесс обучения. Обучение всех моделей выполнялось при помощи оптимизатора Adam (the adaptive moment estimation [15]) с коэффициентом скорости обучения (learning rate), равным 0,001, коэффициентом регуляризации нормы L2 (weight decay), также равным 0,0001, и размером батча 32. В процессе тренировки скорость обучения уменьшалась на 5 % каждые 5 эпох. Каждая из моделей при этом обучалась ровно 75 эпох.

Для каждой рассматриваемой модели проведено три эксперимента по обучению, отличающиеся между собой начальными случайными значениями для гене- ратора случайных чисел (21, 42 и 84). Для каждого случая в качестве финальной модели была выбрана модель, показавшая наилучшие результаты на вали-дационной выборке, а в таблицах представлены усредненные по трем этим экспериментам метрики качества работы. Помимо одиночных моделей, также проведен эксперимент по использованию ансамблей, состоящих из этих трех моделей.

Ансамбль моделей. Существуют различные подходы к организации ансамблей нейронных сетей. В данной работе используется наиболее распространенный подход – невзвешенное среднее ( unweighted averaging [17]). Он заключается в суммировании предсказаний нескольких моделей и применении слоя softmax к полученному вектору значений. Схему комбинирования предсказаний нескольких моделей можно представить следующим образом:

P ( У = k I x ) =

exp ^[ E ^M = 1 P m ⁽ У = ^{k 1} x ) ^]

E ^K — 1 exP ^[ E ^M = 1 P m ⁽ У = ^jIx) ^]

где M = 3 – количество моделей в ансамбле, k – количество классов остеоартрита, а P m (y = k | x) – индивидуальный выход соответствующей модели перед слоем soft-max (ненормированное распределение вероятностей).

7.    Экспериментальные результаты

В качестве метрик качества используются такие характеристики классификатора, как accuracy (процент верно классифицированных изображений, далее и везде по тексту – точность), precision , recall и f 1 -score :

precision =

TP

TP + FP ,

recall =

TP

TP + FN ,

precision ■ recall Fi — 2 ■                        , precision + recall где TP, FP, FN – значения True Positive, False Positive и False Negative из соответствующей матрицы ошибок.

В табл. 4 представлены подробные среднеклассовые метрики для моделей, обученных классификации остеоартрита по рентгенограмме для полной (состоящей из пяти классов) шкале Келлгрена–Лоуренса, а также показана степень улучшения результатов при добавлении SE-блоков. Приведенные значения являются усредненными по трем независимым экспериментам для каждого случая. Префикс SE в названии модели означает, что к традиционной схеме модели были добавлены блоки сжатия и возбуждения – к каждому строительному блоку (residual block) в случае архитектуры ResNet и к каждому плотносвязанному блоку (dense block) для случая DenseNet.

Наилучший результат был достигнут для модели с архитектурой DenseNet-121 и составил 66,73 % для стандартной схемы и 69,77% для расширенного варианта с добавленными блоками сжатия и возбуждения. Добавление SE-блоков в среднем позволило улучшить точность классификации на 1 % – это схоже с выводами, полученными в работе [14]. Наибольшее улучшение на 3,04% было получено для архитектуры DenseNet-121.

Табл. 4. Метрики классификации остеоартрита на тестовой выборке исследуемыми моделями для стандартной шкалы Келлгрена–Лоуренса

Модель	Acc.	Prec.	Recall	F 1	Улучш.
ResNet-18	65,24	0,62	0,65	0,63	-
ResNet-34	66,81	0,65	0,67	0,65	-
ResNet-50	66,42	0,64	0,67	0,64	-
DenseNet-121	66,73	0,64	0,63	0,65	-
SE-ResNet-18	66,02	0,64	0,66	0,64	0,78 %
SE-ResNet-34	67,11	0,65	0,67	0,65	0,30 %
SE-ResNet-50	67,47	0,65	0,68	0,66	1,05 %
SE-DenseNet-121	69,77	0,68	0,70	0,68	3,04 %

Ввиду того, что классы 0 и 1 шкалы классификации при постановке диагноза обычно считаются эквивалентными – и оба трактуются как отсутствие остеоартрита – был проведен эксперимент с объединением этих двух классов в один, при этом остальные классы оставались неизменными. Это позволило улучшить качество работы на 12,74% для лучшей модели и достигнуть среднеклассовой точности классификации остеоартрита 82,51% (табл. 5).

Табл. 5. Среднеклассовые метрики классификации остеоартрита исследуемыми моделями для сокращенной шкалы Келлгрена–Лоуренса из 4 классов ОА
Модель	Acc.	Prec.	Recall	F 1	Улучш.
ResNet-18	79,63	0,79	0,80	0,79	-
ResNet-34	80,13	0,80	0,80	0,80	-
ResNet-50	80,36	0,80	0,80	0,80	-
DenseNet-121	80,86	0,80	0,81	0,80	-
SE-ResNet-18	79,77	0,79	0,80	0,79	0,14%
SE-ResNet-34	80,28	0,80	0,80	0,79	0,15%
SE-ResNet-50	80,29	0,80	0,80	0,80	–0,07%
SE-DenseNet-121 82,51		0,82	0,83	0,82	1,65%

Для случая 4 классов в шкале оценки остеоартрита добавление блоков сжатия и возбуждения также позволило повысить точность, однако значительное ее увеличение (1,65%) наблюдалось лишь для архитектуры DenseNet-121, в остальных же случаях это увеличение было незначительным и находилось на уровне погрешности.

Как было сказано выше, помимо изменения подхода к рассмотрению градации остеоартрита, для повышения точности также было проведено тестирование подхода с использованием ансамбля из трех нейронных сетей с архитектурой SE-DenseNet-121. В качестве агрегирующей функции использовалось невзвешенное среднее. Для обучения моделей использо- вались одни и те же данные, однако для каждого эксперимента использовалось свое начальное значение генератора случайных чисел (в работе это 21, 42 и 84), что позволило получить модели с разными весами.

Среднеклассовая точность классификации при помощи ансамбля ансамбля из трех моделей более чем на 2,5 % превышает усредненную точность одиночных моделей и составляет 84,66% . Подробные метрики качества работы финального ансамбля для каждого класса остеоартрита представлены в табл. 6 – приводятся как значения различных метрик по отдельности для различных классов, так и общие (среднеклассовые) характеристики метода.

Табл. 6. Подробные метрики качества работы для ансамбля из трех моделей SE-DenseNet-121

Класс	Accuracy	Precision	Recall	F 1
1	91,87	0,88	0,92	0,90
2	70,69	0,76	0,71	0,73
3	82,96	0.88	0,83	0,85
4	82,35	0,89	0,82	0,86
Ср.	84,66	0,85	0,85	0,84

Помимо подробных метрик, на рис. 5 и 6 также приводится матрица ошибок и соответствующая ей ROC-кривая со значениями площади под кривой для каждого из четырех классов остеоартрита.

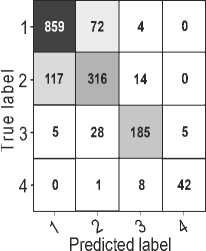
Рис. 5. Матрица ошибок для ансамбля из трех моделей SE-DenseNet-121 для случая 4 классов

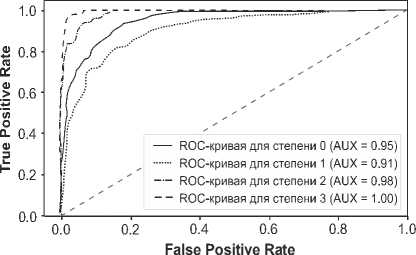
Рис. 6. ROC-кривая для ансамбля из трех моделей SE-DenseNet-121 для случая 4 классов

8.    Обсуждение результатов

В сфере здравоохранения предъявляются очень высокие требования к точности и надежности автома- тических методов диагностики. Несмотря на полученные высокие результаты (с точностью классификации стадии остеоартрита более 84%), их может быть все еще недостаточно для реального применения. Однако несмотря на это предложенные алгоритмы могут быть использованы в качестве вспомогательного инструмента для облегчения работы экспертов.

К примеру, выходной нормированный вектор распределения вероятностей (рис. 7, справа) может быть использован для постановки предварительного диагноза.

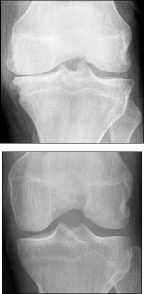
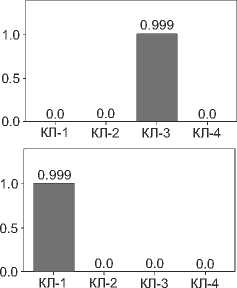
Рис. 7. Распределения вероятностей наличия каждой из степеней остеоартрита на примере

реальных рентгенограмм

Заключение

В работе представлено исследование эффективности добавления блоков сжатия и возбуждения в стандартные архитектуры сверточных нейронных сетей с целью повышения качества их работы. Показано, что использование SE-блоков позволяет повысить точность стандартных архитектур на 1–3 % без существенной модификации готовых моделей, что открывает широкий диапазон возможностей повышения эффективности автоматической классификации.

При этом показано, что эффективность SE-блоков зависит от используемой архитектуры. В частности, встраивание таких блоков в архитектуру ResNet различной глубины для четырехклассовой шкалы Кел-лгрена–Лоуренса не дало какого-либо значимого улучшения точности, в то время как использование их в модели DenseNet-121 в аналогичных условиях позволило повысить качество работы модели на 1,65 % (табл. 5).

Также показано, что объединение 0-го и 1-го классов шкалы Келлгрена–Лоуренса в один класс позволяет существенно (на 12,74 %) повысить точность распознавания прогрессирования остеоартрита. При этом информация по классам, означающим наличие остеоартрита, не теряется, т.к. улучшение происходит за счет объединения двух классов, каждый из которых означает отсутствие заболевания.

Полученные результаты могут быть использованы как для автоматической постановки предварительного диагноза с целью облегчения работы эксперта, так и в качестве вспомогательного инструмента, позволяющего предоставить информацию о возможном распределении вероятностей наличия той или иной стадии остеоартрита у пациента.

К работе прилагаются все обученные модели и исходный код для анализа и воспроизведения результатов исследования, написанный на Python с использованием библиотеки pytorch. Все данные доступны публично на