Использование фотоннокристаллических резонаторов для дифференцирования оптических импульсов по времени

Оптическая реализация базовых вычислительных операций способна повысить уровень аналоговой обработки сигналов [1]. В последнее время были предложены оптические дифференциаторы на основе решёток Брэгга [2], интерферометра [3], кольцевого резонатора [4], дифракционных решёток с волноводным резонансом [5, 6].

В данной работе для исследования оптических резонаторов мы будем использовать временную теорию связанных мод (ВТСМ) [7]. Согласно этой теории исследуемая система представляется набором основных взаимосвязанных компонентов и анализируется исходя из общих принципов, таких как закон сохранения энергии. Поэтому результаты, полученные с использованием ВТСМ, применимы к целому классу рассматриваемых устройств.

1. Постановка задачи и предложенный подход

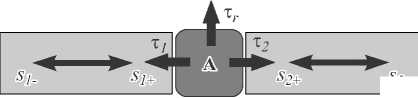
Описание работы оптического резонатора общего вида основывается на двух компонентах. Во-первых, на элементе резонатора, который содержит локализованные моды, возбуждаемые в резонаторе. Во-вторых, на элементах резонатора, которые содержат распространяющиеся моды, закачивающие энергию в резонатор или забирающие её через каналы вво-да/вывода. На рис. 1 схематично показан резонатор с двумя каналами ввода/вывода. В данной работе мы ограничимся этой конфигурацией, хотя приведённый анализ аналогичным образом может быть выполнен для резонаторов с любым количеством каналов вво-да/вывода. Резонансная камера характеризуется резонансной частотой to ₀ и временем затухания т 1 , т ₂ ( т w = т 1 + т ₂), вызванного потерями в каждом из каналов ввода/вывода. Время затухания т r определяет потери на рассеяние в самой камере. Приходящие в резонатор моды и исходящие из него моды описываются комплексными амплитудами s l ± , l — 1,2 . Комплексная амплитуда A характеризует энергию, содержащуюся в резонаторе. Для случая слабого взаимодействия между компонентами системы, при котором A убывает экспоненциально, можно записать следующие уравнения [7]

d A d t

s l —

_A 2 _A 2    ₂

—i to0 A      у--у —sl +, т r    l=i т l     l=i    т l

^— s l + ^{+   2} A .

^т l

Для гармонически осциллирующего электромагнитного поля при условии, что s ₂₊ — 0 , можно получить комплексную амплитуду отражённого поля в одном из каналов

R (to) —

s ₁

i (to — to0) —

I - _ — — —

^т r

1,

1+      i (to — ©0) +т

где 1 т — 1 т w + 1 т r .

»2-

Рис. 1. Схема резонатора с двумя каналами ввода/вывода.

Потери в каждом из каналов ввода/вывода характеризуются временем затухания Т 1 , т ₂ ( T w = T 1 + T ₂). Потери на рассеяние в самой камере характеризуются величиной т . Комплексные амплитуды s l± , l = 1, 2 определяют энергию, приходящую в резонатор и исходящую из него. Комплексная амплитуда A характеризует энергию, содержащуюся в резонаторе

Для определения коэффициентов при производных различных порядков огибающей входного сигнала воспользуемся процедурой, которая аналогична описанной в работах [5, 8]. Разложим комплексную амплитуду отражённого поля в ряд Тейлора. Коэффициенты этого ряда выражаются в виде

т

^R (^to 0 ) = —, ^т r

, П >  0 .

Учёт энергетических потерь резонатора приводит к тому, что в отличие от коэффициентов разложений в работах [5, 8] R ( to ₀) ^ 0 . Для минимизации значения R ( to ₀ ) необходимо, чтобы потери на рассеяние в

резонаторе были значительно меньше потерь через каналы ввода/вывода, т.е. т r » т w .

Для оценки качества дифференцирования используем сигнал с гармонической огибающей, как описано в работе [5], в которой исследовались дифракционные решётки с волноводным резонансом. В отражённом сигнале вес слагаемого, соответствующего производной n-го порядка, равен

E n

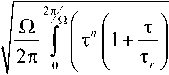
cos ^{( n )}

V

(Qt) dt, / n > 0 . (5)

Здесь величина Q задаёт период сигнала с гармонической огибающей.

После вычисления интеграла данное выражение можно записать в виде т          т + т

E0 = -=-, En = -=-^ тn Qn, n > 0.

V 2 т r         72т r

Критерием оптимизации резонатора, форми- рующего первую производную, является максимизация коэффициента E1 по отношению к сумме остальных коэффициентов. При условии тr >> т1 + т2

это отношение можно записать в виде

E 1 1

£En ~ т2Q2-(т/тr)(1 -тQ).

n * 1

Данное выражение позволяет оценить минимальную длительность импульса, для которой обеспечивается приемлемое качество дифференцирования. Например, если потери на рассеяние меньше потерь на излучение в каналы ввода/вывода на два порядка, т.е. т/т r = 10^-2, то при длительности импульса ~100 пс отношение Е ₁ /^ E_n составляет примерно 100.

/ n * 1

• 2.    Резонатор на основе гребенчатых фотоннокристаллических волноводов

Для иллюстрации вышеописанного подхода к реализации дифференцирующих резонаторов рассчитаем резонатор на основе гребенчатых фотоннокристаллических волноводов (ГФВ) (ridge photonic crystal waveguide) [9]. Резонатор на основе ГФВ представляет из себя плоский волновод, который в области резонансной камеры пронизывают вертикальные отверстия (верхняя вставка на рис. 2). Такой резонатор компактен по сравнению с дифференцирующими резонаторами на основе решёток Брэгга. В отличие от дифракционных решёток с волноводным резонансом поперечные размеры резонатора на основе ГФВ составляют порядка одной длины волны. Кроме этого, резонатор на основе ГФВ легко интегрируется в плоские нанофотонные устройства.

В ГФВ полное внутреннее отражение препятствует распространению света в поперечных направлениях. В продольном направлении отражение света в нанорезонаторе обеспечивает фотонный кристалл [10].

Для создания оптического резонатора с высокой добротностью Q (Q = ю0т/2 ) используем структуру, состоящую из двух частей (верхняя вставка на рис. 2). Во-первых, это фотоннокристаллические зеркала, которые содержат одинаковые равноотстоящие друг от друга отверстия в волноводах. Чем больше этих отверстий, тем меньше потерь в каналах ввода/вывода и, соответственно, больше Qw (Qw = ®отw/2 ). Волновод имеет ширину w =710 нм и высоту h =230 нм. Отверстия в волноводе заполнены воздухом, имеют радиус R = 88 нм и отстоят друг от друга на a = 330 нм. Эти геометрические параметры обеспечивают возникновение энергетической запрещённой зоны (bandgap) для TE-поляризации в волноводе. Данный волновод состоит из кремния (n = 3,46) и окружён воздухом.

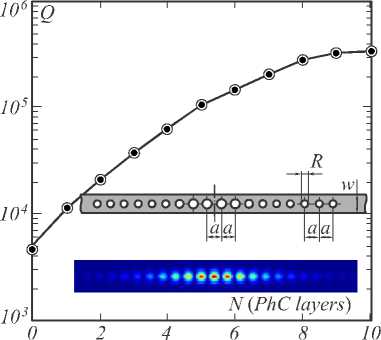
Рис. 2. Зависимость добротности резонатора от количества фотоннокристаллических слоёв в зеркалах резонатора. Верхняя вставка на рисунке изображает структуру рассчитанного нанорезонатора. Нижняя вставка на рисунке показывает распределение модуля электрического поля в рассчитанном резонаторе

Вторым элементом структуры является переходная зона между фотоннокристаллическим волноводом и областью резонансной камеры. Эта зона использована для уменьшения потерь на рассеяние в резонаторе. Величина Qr ( Qr = ю ₀ т r[l^ может быть увеличена минимизацией тех Фурье-гармоник резонансной моды, которые находятся внутри светового конуса волновода [11]. Это достигается изменением коэффициента заполненности ячейки f (f = nR ² / ( aw ))) по квадратичной зависимости. При этом обеспечивается затухание резонансной моды по гауссовой кривизне. Первые 10 отверстий (считая от центра) обеспечивают изменение коэффициента заполненности ячейки от 0,2 до 0,1. При этом радиус отверстий меняется от 155 до 88 нм. Импульсный источник излучения располагается в левой части волновода на рис. 2. Центральная частота импульса составляет 1,2 - 10 6 ГГц (длина волны 1,55 мкм) и соответствует положению запрещённой зоны фотоннокристаллического волновода.

Расчёт характеристик резонансных камер выполнялся с помощью параллельного 3D метода FDTD [12]. По краям трёхмерной расчётной зоны были размещены поглощающие слои. Разрешение вычислительной сетки выбиралось из условия сходимости результатов.

Параметры времени затухания резонатора τ = τ 1 + τ 2 , τ r рассчитывались путём наращивания количества фотоннокристаллических слоёв в зеркалах резонатора. На рис. 2 показана зависимость добротности резонатора от количества данных слоёв. Предел насыщения даёт нам значение т r 10 -10 . Для пяти фотоннокристаллических слоёв в зеркалах резонатора т 10^-12. Дифференцирующий резонатор должен обладать сравнительно невысокой совокупной добротностью Q по сравнению с резонаторами для других приложений [11]. Это позволяет охватывать достаточно широкий спектральный диапазон при обработке коротких импульсов. Небольшая величина добротности резонатора приводит к малой величине отражённого сигнала на резонансной частоте. Используя выражение (4), получим для данного резонатора | R ( ю 0 ) |² 10 -4 .

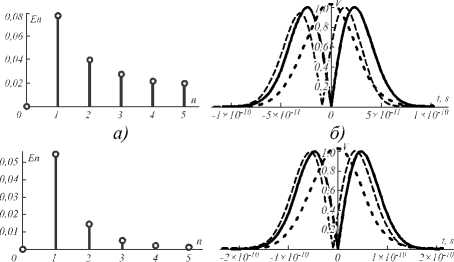
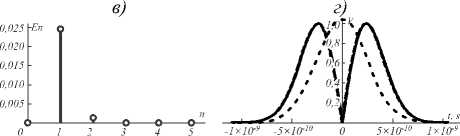
На рис. 3 показаны коэффициенты E_n и результаты дифференцирования импульса, огибающая которого задана функцией exp (- x ² / (2σ²)). График на рис. 3 а показывает первые шесть коэффициентов E_n для сигнала длительностью ~10 пс. Результат дифференцирования такого сигнала рассчитанным нанорезонатором показан на рис. 3 б . Среднеквадратическое отклонение (СКО) между аналитическим (сплошная линия) и численным (линия с длинным пунктиром) результатами составила 21%. Линия с коротким пунктиром показывает исходный импульс. Рис. 3 в , г демонстрируют аналогичные результаты для сигнала длительностью ~50 пс. СКО между аналитическим и численным результатами в этом случае составила 12%. На рис. 3 д , е представлены результаты для сигнала длительностью ~100 пс. СКО составила 2%.

• 3.    Анализ результатов

В работе [13] приведена классификация ранее предложенных дифференциаторов временных сигналов по максимальной частоте дифференцируемых импульсов. Оптоволоконные решётки с большим периодом позволяют дифференцировать сигналы с частотой более терагерца [14, 15]. Оптоволоконные решётки Брэгга способны дифференцировать сигналы с частотой до 10-100 ГГц [8, 16]. Кольцевые резонаторы качественно дифференцируют сигналы с частотой до 10 ГГц. Например, в работе [4] был изготовлен кольцевой резонатор радиусом 40 мкм. Предлагаемый нами нанорезонатор на основе гребенчатых фотоннокристаллических волноводов способен дифференцировать сигналы с частотой до 10 ГГц. При этом размеры данного нанорезонатора (ширина – менее 1 мкм, длина – около 7 мкм) в десятки раз меньше, чем любого из вышеперечисленных устройств. Таким образом, преимуществом рассчитанного нанорезонатора по сравнению с предлагавшимися ранее дифференцирующими устройствами является его компактность и удобство реализации в составе интегральных фотонных устройств.

д)                               е)

Рис. 3. Коэффициенты E_n и результаты дифференцирования импульса, огибающая которого задана функцией exp( -x ²/(2σ²)) . Пояснения – в тексте

Заключение

В работе рассчитан нанорезонатор на основе гребенчатых фотоннокристаллических волноводов, который позволяет с малой погрешностью дифференцировать сигналы длительностью более 100 пс. Полученные аналитические выражения общего вида позволяют оценить качество дифференцирования сигнала для различных параметров нанорезонатора и дифференцируемого сигнала.

Работа выполнена при поддержке грантов РФФИ 10-07-00109-а, 10-07-00438-а, 10-07-00553-а, 11-07-00153-а, 11-07-12051, 11-07-13164-офи-м-2011-РЖД и гранта Президента РФ поддержки ведущих научных школ НШ-4128.2012.9 и ФЦП «Кадры» Минобрнауки (соглашение 8231).