Использование фрактальной модели для оценки микроускорений

Для использования фрактальной модели и оценки с её помощью среднего значения микроускорений как случайного процесса [1]:

W ( t ) = MW + —— M^a ^ ^ C_c_ {( l _{+ s} ) [ shki - sin ki - a (- 2 + chkl + cos kl ) ] + 1 ²        1=1 k,

+

— [ cos k , l - chk ₍l + a, ( shk ₍l + sin k , l )Hcos ( ^ t ) e ^{9 ,1} k , .........J        ^V ' '

, (1)

г де MW – математическое ожидание W ( t ), M_0i и M _{0 i} – соответственно момент, возникающий в заделке упругого элемента в корпус КА от собственных колебаний упругого элемента по i -й собственной форме и его среднее значение, R – радиус-вектор точки расположения технологического оборудования относительно центра масс, I – момент инерции КА, w _i – собственная круговая частота колебаний i -й формы, а b_i – коэффициент затухания, который определяется формулой:

e, =

• 5,    ю, 2 n

= 5Л,,

где 5 i — логарифмический декремент, соответствующий i -й собственной форме.

Необходимо оценить обобщённый параметр z для каждого аппарата, используя формулу [4]:

100 N

z = ------N-----X ^l ,    (3)

m0 + X mJ, i=1

i = 1

где m ₀ — масса КА без учёта упругих элементов, м , – погонная масса упругого элементов, l – длина упругого элемента, N – число упругих элементов.

Тогда с помощью приближённых эмпирических зависимостей [4]:

b « 0,1 z , (4)

D ^ 1,924567 + 0,0075432 M (5) можно оценить параметры действительной части фрактальной функции Вейерштрасса-Ман-дельброта (ФВМ), с помощью которой прелага-

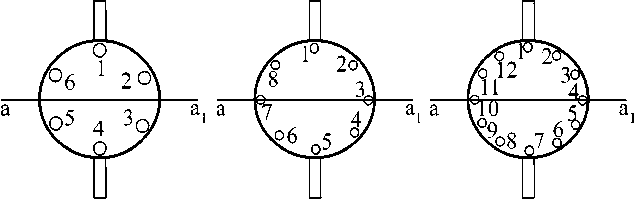
Рис. 1. Схема расположения УРД для моделирования ется аппроксимировать математическое ожидание микроускорений как случайного процесса [5]:

n = +^

Re W (t) = C (t) = £ n = -to

1 - cos ( b n t ) _b (2- D ) n

Для указанных в таб. 1 предполагаемых проектных параметров по формулам (3-5) были рассчитаны параметры фрактальной модели, которые представлены в табл. 2.

Теперь аппроксимация среднего значения микроускорений (первое слагаемое разложения (1)) с помощью ФВМ выглядит следующим образом [2]:

учётом демпфирования в виде модели вязкого трения. Речь идёт о точках, отстоящих от центра масс станции на расстоянии 1 м и максимальному значению момента М, соответствующему включению двигателя №1 на рис. 1.

Оценка первой собственной частоты колебаний по формуле для балки Эйлера-Бернулли:

X =

η2   EI

2π L 2  μ

w = 0,52723 + 0,08835 • C , (6) где w – среднее конечного ансамбля реализа ц ий микроускорений как случайного процесса, а C – среднее ФВМ для фиксированного значения масштабного параметра b и фрактальной размерности D при изменении параметра t в диапазоне от 0 до 1. Так для космической станции типа “Тяньгун-1” эта аппроксимация показана на рис. 2 а без учёта демпфирования в безразмерном времени, для которого t = 0 соответствует моменту выключения УРД, а t = 1 – моменту следующего включения УРД. На рис. 2 б приведены первые 300 с среднего w с

где L , μ и EI – соответственно длина, погонная масса и жёсткость упругого элемента; η - n -й корень уравнения: cos n ch П + 1 = 0 ; n — ^HO" мер тона колебаний.

По формуле для однородной пластины:

3,52 D

2πa2 γh

где a , γ и h – соответственно длина, объёмная плотность и толщина пластины, а D – цилиндрическая жёсткость на изгиб:

D =

Eh3

12 (1 - a2),

Таблица 1. Предполагаемые проектные параметры КА

Парамет р	«Тяньгун-1»	«Фотон-М4»	«Макос-Т»	«Возврат-МКА»
Ди аме тр, м	3,35	2,6	2,5	1,5
Дли на, м	10	3	5	2
Длина ПСБ, м	7,5	4	5	2
Масса, кг	8506	6535	7000-7400	500
Погонная масса ПСБ, кг/м	15	15	30	10
Момен т УРД, Н ⋅ м	9-10	6	7	1
Максимальный ос евой момент ине рции, кг ⋅ м2	70000	30000	32000	1500

Таблица 2. Расчетные параметры фрактальной модели

Парамет р	«Тяньгун-1»	«Фотон-М4»	«Макос- Т»	«Возврат-МКА»
z	2,65	1,84	4,11	7,41
Момен т УРД, Н ⋅ м	9	6	7	2
Масштабный параметр b	0,265	0,184	0,411	0,741
Фрактальная размерность	1,992	1,970	1,977	1,940

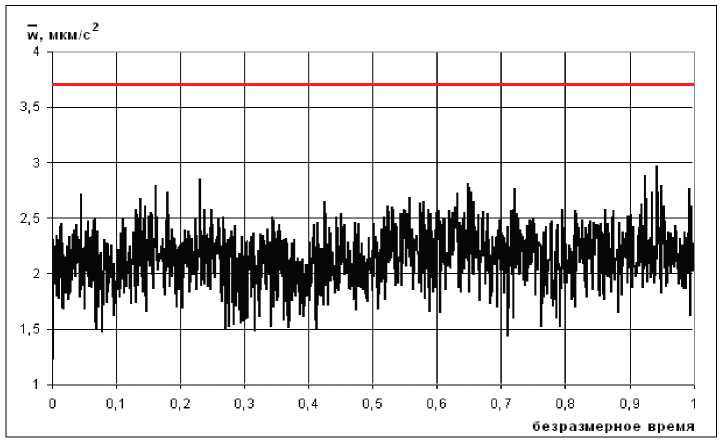
Рис. 2 а. Среднее значение микроускорений без учёта демпфирования для космической станции типа “Тяньгун-1”

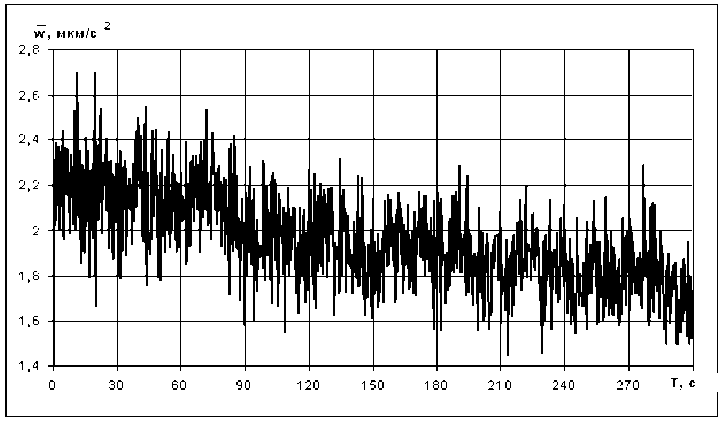
Рис. 2 б. Среднее значение микроускорений с учётом демпфирования для космической станции типа “Тяньгун-1”

где E – модуль Юнга, а σ – коэффициент Пуассона; в результате для материала МА2 значения собственных частот следующие: λ ₁ ≈ 0,00642 Гц и λ ₁ ≈ 0,00762 Гц соответственно. Тогда по формуле:

δω

βi = 2iπi =δiλi, (9)

где δ _i – логарифмический декремент, соответствующий i -й собственной форме. Легко оценить коэффициент затухания, считая δ ₁ = 0,1 [1]: β ₁ ≈ 0,001 .

При справедливости гипотезы о нормальности закона распределения микроускорений в данной реализации, используя правило “трёх сигм”, можно утверждать, что с вероятностью 99,7% текущие значения микроускорений не превысят приблизительно 3,71 мкм/с². Это значение отмечено горизонтальной прямой на рис. 2 а .

Учтём случайность включения УРД, показанных на рис. 1. При включении разных двигателей проекция момента, участвующая в возбуждении колебаний упругих элементов, будет различной. Так при включении двигателя №1 она будет максимальной, а при включении двигателей №3 и 7 на средней схеме рис. 1 и двигателей №4 и 10 на правой схеме рис. 1 она будет нулевой. Следует также отметить, что среднее значение момента зависит и от расположения двигателей по ободу. Сместим линию, проходящую через двигатели №1 и 4 на левой схеме, двигатели №1 и 5 на средней схеме рис. 1 и двигатели №1 и 7 на правой схеме, на угол α от вертикали. Тогда зависимости средних значений проекции момента УРД, участвующей в возбуждении колебаний упругих элементов, и его дисперсии от угла α для представленных на рис. 1 схем расположения УРД показаны на рис. 3 и 4. Это явле-

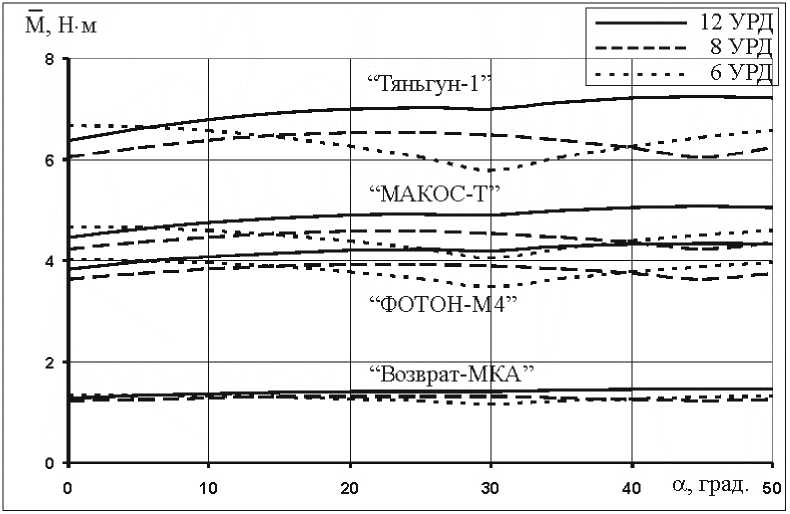
Рис. 3. Зависимость среднего значения проекции момента УРД, возбуждающей колебания ПСБ, от расположения двигателей

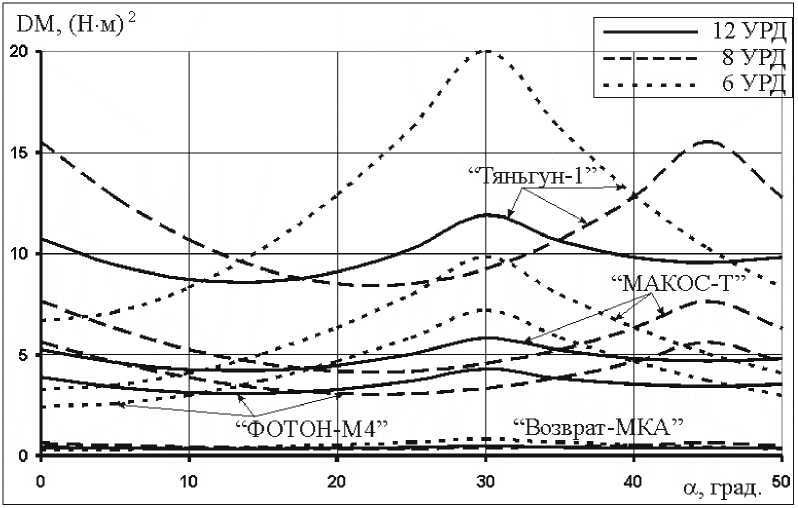
Рис. 4. Зависимость дисперсии проекции момента УРД, возбуждающей колебания ПСБ, от расположения двигателей

ние приводит и к разбросу фрактальной размерности (5) модели. Этот разброс представлен на рис. 5. Поскольку изменение расположения двигателей не повлияет на обобщённый параметр z , то масштабный параметр модели при этом останется неизменным. Это явление приводит к изменению максимального и среднего значений микроускорений внутри реализации (рис. 6). Несмотря на то, что, как видно из рис. 3 и 4, максимальная дисперсия проекции момента УРД, участвующей в возбуждении колебаний упругих элементов, соответствует минимальному среднему значению этой проекции.

Таким образом, можно сделать вывод о влиянии компоновки УРД на микроускорения в реализации. С помощью изменения расположения двигателей можно добиться минимально возможного среднего и максимального значений микроускорений, выполняя при этом задачу ориентации КА.

Для численного моделирования были использованы четыре различных космических проекта, часть исследовательской программы которых посвящено технологическим экспериментами. Проекты были выбраны таким образом, чтобы охватить все виды КА от космических станций (“Тянь-

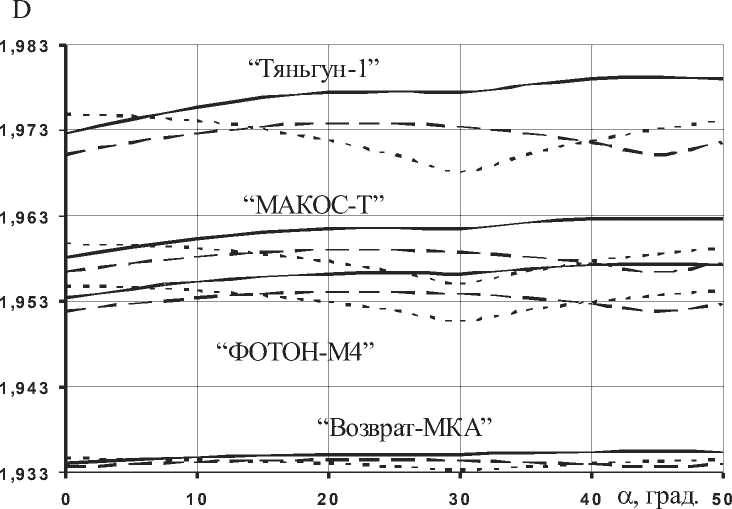
Рис. 5. Разброс фрактальной размерности D, связанный с разбросом параметров момента УРД как случайной величины

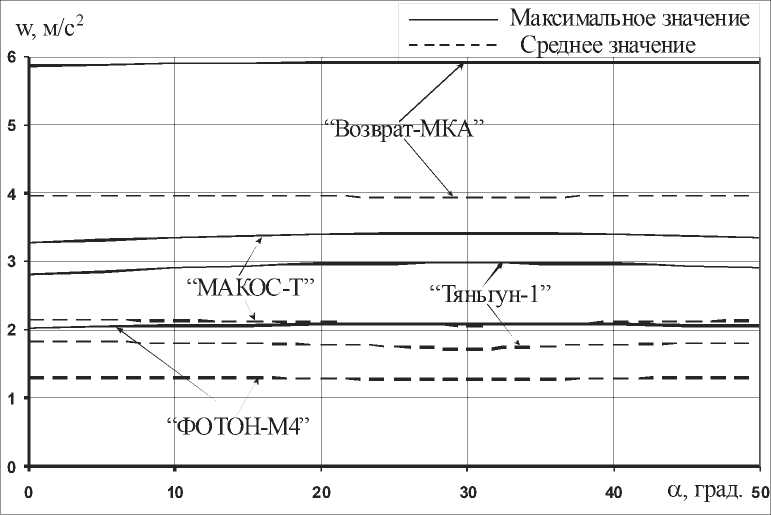
Рис. 6. Изменение среднего и максимального значений микроускорений, связанное с разбросом параметров момента УРД как случайной величины

гун-1”) до малых космических аппаратов (“Воз-врат-МКА”). Это определило большую разницу в массах и моменте УРД рассмотренных проектов (табл. 1). Следует заметить, что предложенная фрактальная оценка может быть использована для моментов УРД, не превышающих значение 10 Н м. В противном случае при M >10 Н линейное упрощение (5) будет давать значения фрактальной размерности D > 2, что недопустимо для ФВМ, фрактальная размерность которой опре- делена границами: 1 < D < 2 - В этом случае следует попытаться найти нелинейную оценку D через М вместо (5) [1]. Однако данное замечание не является существенным недостатком предложенной фрактальной оценки, поскольку значения M >10 Н могут быть характерны для больших обитаемых космических станций, а не для специализированных автономных беспилотных космических лабораторий, для которых и предусмотрена эта оценка.

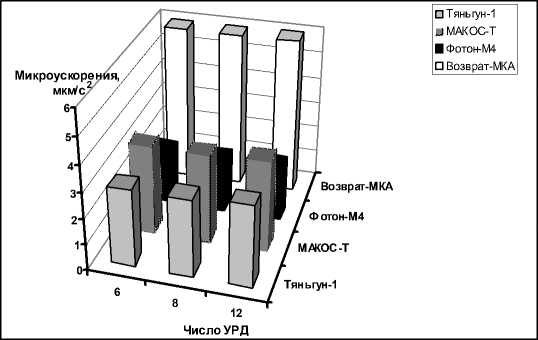
Рис. 7. Динамика предельного значения микроускорений для различных космических проектов

Численное моделирование показало, что не только традиционные конструктивные приёмы, такие как минимизация числа и размера больших упругих элементов, построение такой ККС, в которой реализовано размещение контейнеров с оборудованием как можно ближе к центру масс КА, установка демпфирующих устройств как на узлы крепления ПСБ к корпусу КА, так и технологического оборудования (микрогравитацион-ная платформа) и др., способны снизить уровень микроускорений внутренней среды. В некоторых случаях оптимальное размещение УРД также является эффективным конструктивным приёмом. На рис. 7 показана динамика предельного значения микроускорений, выше которого в случае справедливости нормального закона распределения с вероятностью 99,7% не выйдет текущее значение микроускорений для рассмотренных проектов КА. Если для “Тяньгун-1” можно добиться снижения уровня микроускорений оптимизацией расположения УРД более, чем на 6% при абсолютном значении предельного уровня примерно 3 мкм/с2, то для “Возврат-МКА” – менее, чем на 1% при абсолютном значении предельного уровня примерно 6 мкм/с2.

На основании проведённых исследований можно сформулировать метод оценки микроускорений и динамики космической лаборатории технологического назначения с упругими элементами конструкции в следующем виде:

• 1.    По заданным проектным значениям массы КА, погонной массы и длины ПСБ вычислить обобщённый параметр z с помощью (3).

• 2.    По вычисленному значению обобщённого параметра z оценить значение масштабного параметра ФВМ b , используя приближённую зависимость (4).

• 3.    По заданному проектному значению момента УРД М оценить фрактальную размерность ФВМ D с помощью приближённой зависимости (5).

• 4.    На основе оценённых значений параметров ФВМ построить функцию как оценку среднего значения микроускорений без учёта демпфирования (рис. 2).

• 5.    По заданным проектным параметрам ПСБ оценить собственные частоты колебаний всех учитываемых форм с помощью (7) для балочной схемы, (8) для однородной пластины или конечно-элементной модели.

• 6.    С помощью справочных или экспериментальных данных для заданного материала каркаса ПСБ оценить логарифмический декремент по каждой учитываемой форме колебаний.

• 7.    По рассчитанным значениям логарифмических декрементов вычислить коэффициенты затухания по каждой учитываемой форме колебаний с помощью (9).

• 8.    С помощью зависимости (6) оценить математическое ожидание микроускорений как случайного процесса, используя также проектные параметры и ранее вычисленные величины.

Построенный метод может быть использован для оценки микроускорений на спроектированном КА. В случае несоответствия оценённого уровня микроускорений требуемому, необходимо оптимизировать параметры КА, влияющие на динамику вращательного движения КА вокруг центра масс, с целью снижения микроускорений. Оптимизацию следует проводить с учётом требований к ориентации КА, а также его энерговооружённости.

Таким образом, в работе показано применение фрактальной модели оценки среднего значения микроускорений для четырёх космических проектов, выявлено влияние расположения двигателей УРД относительно больших упругих элементов на среднее значение создаваемых микроускорений, а также построен метод оценки среднего значения с помощью фрактальной модели.