Использование функций чувствительности для расчета включений трубок траекторий управляемых систем
Автор: Рогалев А.Н.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 2 т.17, 2016 года.
Бесплатный доступ
Рассматриваются вопросы применения функций чувствительности для вычисления границ включений множеств достижимости управляемых систем в задачах оценки предельных отклонений летательных аппаратов: самолета, ракеты, космического корабля. Как правило, в рамках теории чувствительности проводится численное исследование параметрической модели управляемой системы во всем диапазоне изменения определяющей совокупности параметров. Практическое применение такого подхода очень часто оказывалось нецелесообразным или невозможным из-за огромного количества требуемых вычислений и необозримости получаемых результатов. Предложенное и реализованное в статье совместное применение функций чувствительности и символьных формул решений позволяет эффективно вычислять включения множеств достижимости - совокупностей концов всех траекторий управляемой системы, начинающихся в начальный момент времени в точках начального множества. Эти множества применяются в задачах гарантированного оценивания совокупностей отклонений летательных аппаратов и задачах контроля предельных отклонений, при этом действующие на систему внешние возмущения и ошибки наблюдения заключены в определенных пределах (стеснены ограничениями). Под функциями чувствительности понимаются производные различных переменных состояния и показателей качества по параметрам соответствующей и определяющей группы. Эти функции являются решениями уравнений чувствительности, которые могут быть непосредственно получены из известной параметрической модели системы. Описанный в статье метод, использующий символьные формулы решения и функции чувствительности, позволяет получить надежную оценку множеств достижимости управляемых систем в условиях неопределенности, если в правые части этих систем управляющие воздействия входят произвольным образом, не только как аддитивный член. Область применения этого метода включает задачи оценки предельных отклонений при движении самолета на этапе автоматического захода на посадку, задачи определения возможности потери устойчивости движения летательного аппарата на заданном интервале времени, т. е. задачи траекторной безопасности летательного аппарата, задачи посадки вертолета. Упрощенным критерием потери устойчивости в подобных задачах служит вычисление некоторого порогового или критического значения одного из параметров движения и оценки границ областей всех возможных траекторий. Представлены результаты применения численных методов, основанных на символьных формулах решений и функциях чувствительности и оценивании всех возможных ее значений.
Предельные отклонения траекторий, летательные аппараты, критические значения параметров, гарантированный метод оценивания, символьная формула, функция чувствительности
Короткий адрес: https://sciup.org/148177568
IDR: 148177568 | УДК: 517.977.1
Текст научной статьи Использование функций чувствительности для расчета включений трубок траекторий управляемых систем
Введение. Рассмотрим управляемую систему, движение которой описывается системой обыкновенных дифференциальных уравнений (ОДУ)
dy = f (t, У, u), u (t) e U, У (t °) = У °, (1) dt в правой части которой задано ограниченное по величине управляющее воздействие и и поставлены начальные данные. Налагаем на задачу (1) ограничения: f - непрерывно дифференцируемая по у функция (f (t) e C 1), множество U компактно в Rm , выбор возможных реализаций управляющих воздействий и(•) стеснен ограничениями и(t) e U,t e [t°,t], отражающими особенности рассматриваемой задачи. Кроме того: а) выполняется равномерная оценка | у(t) |< b для всех решений (1) на интервале t e [t°,T], где b = const > °; б) множество Y(t) = = f (t, у, U) для всех у , t e [s, T] компактно и выпукло.
Множеством достижимости D ( t , t ° , M ) управляемой системы (1) с начальным условием у ( t ° ) = = у ° e M при t > t ° называется совокупность концов у ( t ) всех траекторий этой системы в момент времени t (рис. 1), начинающихся в момент s в точках начального множества M [1-3].
Непрерывность множества достижимости D ( t , t ° , у ° ), зависящего также от времени, означает следующее: для любого £ > ° существует 5 > ° такое, что хаусдорфова метрика между множествами значений решений в моменты времени 1 1 , t 2 становится меньше £ :
d ( D ( 1 1 , t ° , у ° ), D ( t 2, t ° , у ° )) <£ , 1 1 1 - 1 2| <5 , 1 1 , t 2 e [ t ° , T ].
Множества достижимости играют важную роль в теории управляемых систем. Эти множества позво ляют формулировать и решать многие основные задачи теории управления [1-7]. К подобным задачам относятся задачи проверки гарантированных условий безопасности и задачи построения «выживающих» траекторий. Условие «выживаемости» означает проверку выполнения условий у(t) e N при t° < t < T для любого движения y(^), исходящего из точек области допустимых начальных позиций Y°, и заданном множестве N при переборе всех управляющих воздействий, удовлетворяющих ограничению и(•) e Q .
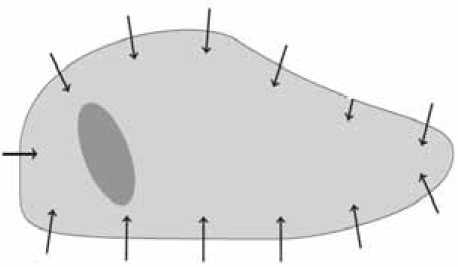
Рис. 1. Совокупность концов у ( t ) всех траекторий системы (сечение) в момент времени t , начинающихся в момент s в точках начального множества М -множество достижимости
Значительно чаще на практике рассматривается управляемая динамическая система общего вида, подверженная к тому же действию неопределенных факторов. Тогда движение такой системы подчиняется следующей системе дифференциальных уравнений:
dУ = f (t, У, u, v), (3)
dt где u = u(t) - управляющее воздействие; v = v(t) -неконтролируемое воздействие. Вообще говоря, величины векторов управлений и возмущений (допустимых управлений и возмущений) могут быть сложным образом связаны с движением динамической системы. Мы будем рассматривать лишь случай геометрических ограничений, имеющих вид u е U(t, x), v е V(t, x).
Зная границы множеств достижимости, можно найти зависимость разрешимости рассматриваемых задач от начального множества M , времени T , множества N и т. д. Такие задачи часто возникают на практике, например, при оценке возможностей маневра летательных аппаратов (ЛА) [8]. Просчитав (или оценив) траекторию, можно узнать, выполняются ли некоторые интересующие нас свойства. Одним из таких свойств является безопасность объекта. Можно сформулировать так: траектория у ( t ) безопасна, если она не имеет точек пересечения с «опасным» множеством F , выполняется ограничение V t > 0, У ( t ) 6 F .
Точки пространства состояний, попадание в которое для управляемой системы означает аварийное завершение, составляют область F (на рис. 2 эта область закрашена черным цветом). Такие области описываются в зонах так называемого сваливания самолетов, а также при анализе процесса автоматической посадки самолета, в первую очередь сводящейся к оценке возможных значений параметров траекторного и углового движения самолета в момент касания шасси взлетно-посадочной полосы (ВПП). Для подобных задач необходимо оценить максимальное значение одного из параметров не в фиксированный момент времени, а на определенном интервале времени полета. При этом на ЛА воздействуют различные влияющие, в том числе друг на друга, возмущения: отклонения инерционных и аэродинамических параметров ЛА, атмосферные возмущения, инструментальные ошибки, отказы и т. п. Задачи такого типа в [8] называют задачами о выбросах случайного процесса.
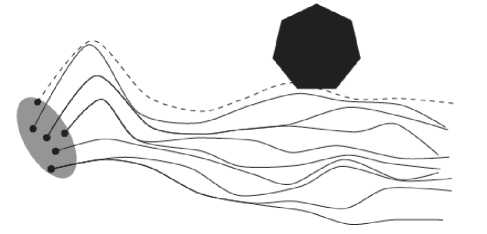
Рис 2. Совокупность (пучок) всех траекторий управляемой системы, начинающихся в точках начального множества, и «опасное» множество, закрашенное черным цветом
Выделяется два подхода к решению задач, контролирующих предельные значения или предельные реализации. Первый подход реализует случайный характер возмущений и является широко распространен ным [8]. Для второго подхода - гарантированного подхода - возмущения представляют собой набор конечного числа случайных параметров, для значений которых поставлены вполне определенные ограничения, и пусть заранее известно, что зависимости выходных параметров от любого из упомянутых параметров являются монотонными. Это означает, что выходные параметры достигают экстремальных значений при сочетаниях граничных значений случайных параметров определенного знака. На основе экстремальных значений вычисляются соответствующие значения выходных параметров. Если окажется, что выходные параметры не выходят за допустимые пределы, то выполнение всех ограничений можно считать гарантированным. Если возмущениями являются систематические инструментальные ошибки, а используемые бортовые (и наземные) приборы прошли предварительную проверку и тарировку, то гарантированный подход может быть полностью обоснован. Можно полагать, что ошибка в показаниях того или иного прибора не превосходит допустимых пределов. При этом закон распределения некоторой инструментальной ошибки Де часто сильно отличается от гауссовского закона за счет того, что в процессе доводки прибора ошибка изменяется внутри разрешенного диапазона. В этом случае распределение ошибки оказывается ограниченным и может иметь пики в окрестностях предельных значений.
Расчет включений трубок траекторий и множеств достижимости управляемых систем. В статье описаны методы, основанные на совместном использовании символьных формул решений и функций чувствительности, цель этих методов - вычисление гарантированных границ множеств достижимости и применение этих границ для оценки предельных отклонений траекторий ЛА. Вычисление границ множества Y(t) = ^ у(t, у0) позволяет гарантированно у 0еГ 0
оценить множество достижимости управляемой системы (3) с учетом неконтролируемых возмущений. Определение границ (включений множеств достижимости) основано на символьных формулах, аппроксимирующих оператор сдвига вдоль траектории, а также на формулах производных решений по параметрам системы (в том числе начальным данным) с последующим вычислением множества значений символьных выражений. Используемые при этом свойства функций чувствительности управляемых систем описаны в [9-12]. Многие вопросы, касающиеся обработки символьных преобразований в гарантированных методах, описаны в работах [13-22]. В данной статье включены новые дополнительные варианты конструирования зависимостей между значениями решений управляемых систем и их начальными значениями, а также управляющими параметрами этих систем.
Для качественного анализа решений и определения необходимых динамических характеристик задачи (3) приведем конструктивные функции использования чувствительности.
Пусть ai, ...,am - фиксированные значения параметров, их множество будем называть основной или базовой совокупностью. Выбранной совокупности а соответствует совокупность переменных состояния
Yi = y ( t , а ), (4)
которую будем называть основным или базовым движением. Базовому движению соответствуют базовые значения показателей качества J i = J i ( а ), в нашем подходе показателями качества считаем максимальные и минимальные значения всей совокупности движений. При изменении значений параметров a i = = а i + ц i получим новое движение
Yi = Yi (t, ат + ц1,..., am + ц m) = Yi (t, а + ц),(5)
которому соответствуют новые значения показателей качества
Ji = Ji (ат + ц1,..., а m + ц m) = Ji (а + ц).(6)
Определение . Вектор A Y i , определяемый соотношением
A Y = Yi (t, а + ц) - Yi (t, а),(7)
как правило называется дополнительным движением, вызванным изменениями параметров а т,..., а m .
Дополнительное движение AYi и соответствующие приращения показателей качества aji=J (а+ц) - J (а) (8)
характеризуют изменение интересующих исследователя свойств системы при изменении соответствующих параметров. Поэтому изучение свойств дополнительных движений и установление их связей со свойствами исходной системы является, по существу, основной задачей исследования чувствительности. Для вывода зависимости между функциями чувствительности и дополнительным движением используются свойства дифференциалов высших порядков функций многих переменных [9; 10].
Для функции многих переменных Y = Y ( x1, ..., x n ), имеющей частные производные k -го порядка по всем совокупностям аргументов x 1, ..., x n , дифференциалом k -порядка называются выражения
k
(а1
d(k)y = 1 — dx1 +... + — dxr I Y,(9)
^ axT axr)
где — - операторы дифференцирования по соответ-axi ствующим переменным. Для развертывания выражения (9) следует формально возвести в степень выражение в скобках, свернув произведение операторов по правилу a a a2
a x, a x j a x i a x j
а затем применить полученный оператор к функции Y .
Из (9), (10) следует, что k-й дифференциал является формой k -й степени относительно величин dx1, ...,dxr . Предполагая, что в точке а существуют и непрерывны по параметрам все функции чувствительности до (k +1)- го порядка включительно, можно написать выражение по формуле Тейлора с остаточным членом
A Y ( t , а ) = Y ( t , а + ц ) - Y ( t , а ) =
= dY ( t , а ) +^ d (2) Y ( t , а ) + ^ d (3) Y ( t , а ) + (11)
+ ... + —1— d ( n + 1) Y ( t , а + Оц ).
( n + 1)!
Заметим, что в формуле (11) переменная t считается неизменным параметром. Пренебрегая остаточным членом, из (11) получим приближенное выражение для дополнительного движения k
A ( k ) Y ( t , а ) = £ - d': Y ( t , а ) , (12)
i =1 • а=а которое будем называть k-м приближением для дополнительного движения или, что эквивалентно, приближением с точностью до величин (k + 1)-го порядка малости.
Напомним, что символьной формулой (аналитическое выражение) [13; 15] называется запись имен переменных и совокупности действий, которые нужно проделать в определенном порядке над значениями этих переменных. В дальнейшем при записи символьных формул, аппроксимирующих оператор сдвига вдоль траектории, допускается включение в них числовых констант с отложенным выполнением арифметических действий над ними.
Пусть Ki - последовательность нормированных пространств, зависящих от параметра и , принадлежащего множеству U ; Y1 , i = 1, ..., n - 1, - последовательность символьных формул непрерывных отображений F , определенных на прямом произведении K 1 х K 2 х х ... х K n , которые отображают это произведение в пространство K n +1 и задают зависимость между значениями решения в каждой точке области определения и начальными значениями решения. Результат последовательного исполнения преобразований формул
Y 1 = F 1( t 0, t 1, Y 0, Y 1) = S 1( Y 0),
Y 2 = F 2( t 0, t 1, t2, Y 0, Y 1, Y 2) = S 2( Y 0) о S 1( Y 0),
Y ‘ = Fi(t°,...,ti,Y0,YV..,Yi) = Si(Y0)о_о о S 2( Yi-1) о S 1( Y1), (13)
Ym = Fm (t0,., tm, Y0, Y1,. Ym) = Sm (Y0) о.о о S 2( Yi-1) о S 1( Y1i)
будет называться символьной формулой (опорной траекторией) метода, заданной сдвигом вдоль траектории ОДУ.
Включение в правую часть управляемой системы управления и , принадлежащего произвольному множеству U , позволяет учитывать все управляющие воздействия при построении множеств достижимости управляемых систем.
Итак, метод записи и преобразования символьных формул основан на следующих шагах:
-
1. Запись компонент символьных формул решений как векторных функций, состоящих из символьных компонент ^ ( t k ), зависящих от символьных форм начальных данных yj, ..., y j. Каждая компонента символьного вектора определяется заново в каждой точке t k как функция, зависящая от символьных начальных данных y j, ..., y j. Эта формула описывает сдвиг вдоль кривой, аппроксимирующей траекторию решения системы, на каждом шаге.
-
2. Последовательное исполнение метода хранения и переработки символьной информации при продвижении вдоль траектории решений, производящееся на основе статичного хранения этой информации, работы с адресацией памяти с помощью функций поточной обработки.
-
3. Преобразование символьной формулы приближенного решения к виду, который позволяет эффективно и быстро вычислять оценки областей значений приближенных решений ( 5 -решения), соответствующие изменениям параметров задачи. Для этого используется кусочно-полиномиальное представление символьных формул и опорные функции для многозначных функций, описывающих области значений. Символьные формулы не преобразуются на каждом шаге алгоритма, организуется их хранение в памяти, для этого полезным является кусочная полиномиальность.
За описанным выше алгоритмом получения символьных формул следует шаг вычисления областей их числовых значений
На каждом шаге по времени решаются ” различных систем уравнений в вариациях первого порядка
d 6 у* = 6
dt 6
5 f i ( t , Ф 1 , Ф 2 ,
5 y j
^•б y j , i = 1, 2, ..., ” . (15)
Для получения этих систем следует отметить, что вначале все компоненты вектора неизвестных дифференцируются по у 0 , затем по у 0 , в последней системе все компоненты дифференцируются по у ” . Это означает, что на первом шаге этого этапа система (15) решается относительно вектора неизвестных
T
I 5у, 5у2 5у35
—й,—2,—3,..., —”" с начальными данными 0 0 00
(5У1 5У1 5У1
У 1 ( tk ) = 1, У 2 ( tk ) = 0, ., У ” ( tk ) = 0, на втором шаге
система (15) решается относительно вектора
T
I 5у, 5у2 5Уз 5y„ I неизвестных —-,—-,—-,..., —- с начальными
„5 У20 5Уj 5У20 5У 20 J данными У1(tk) = 0, У2(tk) = 1, ., У”(tk) = 0, .., наj-м шаге система (15) решается относительно вектора
неизвестных
5 У 1 5 у 2 5 у з о 0 , о 0 , о 0 „5 У j 5 У j 5 У j
T
5 У ”
5 уУ,
с начальными
данными У 1 ( tk ) = 0, у 2( tk ) = 1, ... y j .( tk ) = 0, ..., У ” ( t k ) = 0.
Система (15) - это линейная система ОДУ с постоянными коэффициентами
У ” = F" ( t 0,..., t ” , Y 0, Y 1 , . У ” ) = = 5 ” ( У 0) о.о 5 2(У ) о 5 1 У ),
5 f i ( t , Ф 1 , Ф 2 , ..., Ф ” )
5 T j
для чего используется следующая методика обработки последовательности символьных формул.
Для системы (3) с начальными данными у ( t i 0) = У 0 е У °, i = 1, 2, ...., ” строится сетка узлов на интервале интегрирования с точки t i = t 0 + i • h , i = 1, 2, ..., n , и вводятся обозначения
Постоянные коэффициенты получаются при подстановке в формулы производных вычисленных значений ф 1 , ф 2, ..., ф ” .
Аналогично на k -интервале по времени вычисляются векторы решения (всего ” различных векторов при k = 1, 2, ..., ” )
„ 0 0 Оч
у* = Ф i ( t , У 1 , У 2 , ..., У ” ),
, _ 5Фi „0 „0 „Оч zi „ о( t’ У1 , У 2, ..., У” ),
-
5 У к
-
5 2ф / , 0 0 0 ч
w i = о 42 ( t ’ У 1 ’ У 2 , -’ У ” ),
5 ( Ук)
5zx
6 z 1 =
5 У /
6 z 2
6 z ”
5 2 ф 1 ( tk , у 1 0, у j , ..., y j )
,
6 У А '
5 У к
. _ 5 z ,
6 z* А 0
5 У /
5ф i ( t k , У 1 0, У 0 , ..., У 0 ) 0
я2„ кА 0 0 0ч
-
5 Ф i ( t , У 1 , У 2 , ..., У ” ) 0з 0
-
6 w i
5 w i
-
■■
53ф * ( tk , y j , у j , ..., У ” 0)
5У° т 5 У 0 5 у к
5 z 2 5 У / 0
5 У ”
5 у/
5 y j 5 y j
5 2 ф 2 ( tk , y j , y j , ..., y j )
5yj5yj k 00 0
5Ф ” ( t , У 1 , У 2 , ..., У ” )
5 у /
,
различных систем уравнений в вариациях второго
порядка с нулевыми начальными данными:
d6z* =^у 5fi(t,Ф1,Ф2, ...,Ф”) •gz + dt j=1 5yj
nn
+ 6 6
52У ( t , Ф 1 , Ф 2 , ..., Ф ” ) 5Ф ,
‘ 0 ^6 y , 5Ук
5 y j 5ys
i = 1, 2, ..., ” , k = 1, 2,..., ” ; / = 1, 2,..., ” .
Количество систем вида (16) равно биномиальному коэффициенту с П сочетаний из числа п по 2.
Система (16) - это линейная система ОДУ с постоянными коэффициентами
8 f i ( t , Ф 1 , Ф 2 , ..., Ф n ) 8 2 ft ( t , Ф 1 , Ф п , ..., Ф n )
8 y j ’ 8 y j 8 y$ ’ (17)
i = 1, 2, ..., n ; k = 1, 2, ..., n ; l = 1, 2, ..., n .
Числовые значения этих коэффициентов определяются при подстановке в формулы производных вычисленных значений ф 1 , ф 2, ..., ф п .
Продолжая подобным образом, на основе полученных значений производных записывается символьная формула решений как функция от начальных данных 0 0 0х.
( У 1 , У 2 , — , У п ):
2) для участка автоматического управления построить область W возможных состояний системы на ВПР, куда гарантируется попадание при любых допустимых, в том числе экстремальных, возмущениях.
Если вложение D с W справедливо, система обеспечивает управление самолетом с необходимой точностью. Поскольку наибольшие трудности вызывает устранение накопившихся к концу участка боковых отклонений [24; 25], то имеет смысл рассмотреть отдельно случай бокового движения самолета.
о „.о о о si (у1 , ..., yn ) = фi (y1,num, ..., yn,num) Н о о о о о о .
+ ( У 1 - У 1,пит ) б У 1 + ( У 2 - У 2,num ) § У 2 +
+ --- + (у о-уо )5у° + уп yn ,num yn
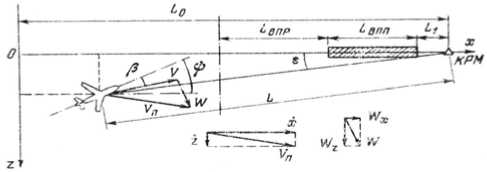
Рис. 3. Положение самолета при заходе на посадочную прямую
н—
2!
( У ° - У 1 0 num )2 § z 1 + ( У ° - У 2 0 num )2 § z 2 +
+ - + ( У 0 - У ' § z n + (18)
о _. о о _ о
Н 2( y 1 y 1,num )( y 2 y 2,num )
я 2 о о
8 Ф i ( У 1 , ..., У п )
8 Уй ° 8 у °
+
+ ... + 2( У ° - 1
—
0 0 _ о yn -1,num )( yn yn ,num
)
я 2 0 0
8 Ф i ( У 1 , ..., У п )
8У0п-18уП
.
Для формул вида (18) решается задача на экстремум, т. е. разыскивается максимальное и минимальное значения функции s i ( у ° , ..., y ° ), зависящей от начальных данных ( y ° , у ° , — , y ° ) как от независимых переменных. В формулу, описывающую функцию, входят выбранные числовые значения /00 О X
( У фт™ , У 2,num , — , Уп ,™™ ' и вычисленные р анее числа 2 0 е 0 2 0, с 0 с 0 2 0 0 0 0
§ У 1 , § У 2 , ..., § У п ; § Z 1 , § z 2 , ..., § Z n ; § W 1 , § W 2 , ..., § W n . В силу сказанного функция s i ( y ° , ..., y ° ) является полиномиальной функцией от многих переменных.
Примеры включений трубок траекторий и множеств достижимости управляемых систем
1. Для самолетов участок траектории захода на посадку, остающийся после перехода на ручное управление, очень мал, и полет происходит на малой высоте. Это означает, что возможности корректировки накопившихся отклонений весьма ограниченны. Поэтому к моменту принятия решения необходимо вывести систему в некоторую область пространства состояний.
Можно выделить две связанные друг с другом задачи [23-25]:
1) построить область D допустимых отклонений на ВПР, из любой точки которой за оставшееся время самолет может быть выведен при ручном управлении на участок ВПП, отведенный для посадки;
Чтобы сократить выкладки, исследуем только последний участок траектории захода на посадку - предпосадочную прямую. Положение самолета (рис. 3) определяется координатами его центра масс в системе координат xOz , связанной с землей, углом рыскания ф и углом крена у . К фазовым координатам относятся также скорости изменения этих величин Z, ф , у . Предполагается, что ось Ox совпадает с продольной осью ВПП. Тогда величина z характеризует боковое уклонение центра масс самолета от оси ВПП (рис. 3). Управляющими воздействиями являются отклонения элеронов (угол § э) и руля направления (угол § н). К возмущениям, непосредственно действующим на самолет, также относятся изменения боковой составляющей скорости ветра Wz (действием вертикальной Wy и продольной Wx составляющих скорости пренебрегаем).
Учитывая малость отклонений самолета от заданной траектории, запишем уравнения бокового движения самолета [24; 25]:
d 2 z
— = azрр + azуУ + az§н§н , dt2 н d2 ф
—Г = a фР₽ + a фФ + a фу У + a ф§н §н + a ф§э §э , d 2 у dty = a урР + a Уф Ф + a у У + a у§н §н + a у§э §э ,
где Р = ф +
z - Wz V
- угол скольжения, т. е. угол между
вектором воздушной скорости V и продольной плоскостью самолета. Коэффициенты a j определяются аэродинамическими параметрами самолета, такими, например, как площадь крыла, размах крыла, масса самолета, моменты инерции относительно соответствующих осей, скоростной напор, плотность воздуха,
безразмерные аэродинамические коэффициенты, производные коэффициентов по соответствующим переменным.
Характерные значения предельных отклонений вероятностей превышения для стандартных размеров ВВП [25] с целью проведения тестовых расчетов выглядят следующим образом.
Минимальная дальность касания от среза ВВП L = 60 м, р, = 10 6 . Максимальная дальность шш L min
L max = 900 м, p L^^ = 10 6. Боковое смещение от оси
ВВП z = 21 м, р, = 10 6. Минимальный угол тан-шах z гажа Tmin определяется условием касания ВПП передней стойкой шасси раньше, чем основными стойками р = 10 8. Максимальный угол тангажа Э »min шах определяется условием касания хвостовой частью фюзеляжа самолета ВПП раньше, чем основными стойками шасси р = 10 8. Максимальный угол Эшах крена у max определяется условием касания поверхностей земли крылом или двигателем самолета под крылом р= 10 8. На рис. 4 представлены границы включений областей допустимых отклонений под влиянием быстрых изменений скорости бокового ветра. При выборе области допустимых начальных состояний объекта предполагаем, что управляющее воздействие выбирается так, чтобы по возможности увеличить размеры области, а возмущение стремится уменьшить их.
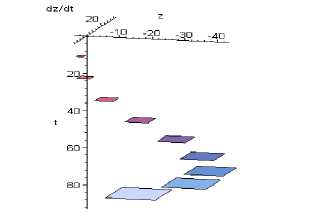
Рис. 4. Граница включений угла скольжения самолета часто рассчитываются заранее, задаются в виде массивов для конкретного вертолета (вместе с постоянными параметрами).
При этом заданы начальные значения фазовых переменных, ограничения на управление и значения фазовых переменных в конце маневра:
ui < U1 < ui, i = 1,2, y(tF) < у^ , y 2 (tF ) — у 2 , у 3 (tF ) — у 3 .
Требуется минимизировать конечную высоту h ( tF ), что равносильно максимизации нижней границы опасной зоны аварийной посадки.
Вводя весьма жесткие ограничения на переменные состояния, получают достаточно узкие грубые рабочие диапазоны изменения этих переменных. Это дает основание принять в качестве сравнительно грубой аппроксимации модели движения на этапе качествен ного анализа линейную конструкцию — = Ay + Ви + dt
+ C , где А , В , C - матрицы.
С учетом этих допущений линейная аппроксимация модели принимает вид dyAdy
—— = -9,8 u1, —— = a 21 у1 + a 22 у 2 + a 23 у 3 + b22 и 2 + c 2, dtdt dy3 ,
~Г = a31 у1 + a32 у2 + a33 у3 + b32и2 + c3 , —Т" = у2 ■ dtdt
Для величин a j , b j , c j известны их конкретные числовые значения [26].
Применяемый для оценки областей достижимости управляемой системы метод, основанный на построении символьных формул и функциях включения, позволяет просчитать включения областей достижимости летательного аппарата и предложить для проверки границы опасной зоны полета или аварийной посадки. Границы опасной зоны полета или посадки вертолета определяются по-разному в зависимости от многих случаев, например, как максимально допустимая высота маневрирования над ровной поверхностью и над препятствием и т. п. Далее приведен график расчета границ в модельном примере (рис. 5).
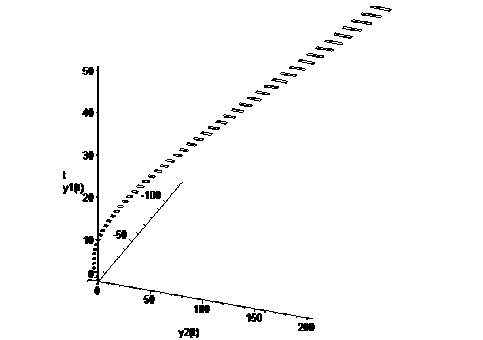
Рис. 5. Оценка сверху опасной зоны аварийной посадки вертолета (высоты и угла маневрирования над препятствием)
Заключение. В статье описаны методы, основанные на совместном использовании символьных формул решений и функций чувствительности. Целью методов является вычисление гарантированных границ множеств достижимости и применение этих границ для оценки предельных отклонений траекторий ЛА, при этом учитываются как параметры управления, так и неконтролируемые возмущения. Определение границ (включений множеств достижимости) основано на символьных формулах, аппроксимации оператора сдвига вдоль траектории, а также на формулах производных решений по параметрам системы (в том числе начальным данным) с последующим вычислением множества значений символьных выражений. В статье рассматриваются новые дополнительные варианты конструирования зависимостей между значениями решений управляемых систем и их начальными значениями, а также управляющими параметрами этих систем.
Список литературы Использование функций чувствительности для расчета включений трубок траекторий управляемых систем
- Куржанский А. Б. Управление и наблюдение в условиях неопределенности. M.: Наука, 1977. 392 с.
- Черноусько Ф. Л. Оценивание фазового состояния динамических систем. М.: Наука, 1988. 319 с.
- Chernousko F. L. State Estimation for Dynamic Systems. Boca Raton: CRC Press, 1994. 304 p.
- Овсеевич А. И., Шматков А. М. К вопросу о сопоставлении вероятностного и гарантированного подходов к прогнозу фазового состояния динамических систем//Известия Академии наук. Теория и системы управления. 2007. № 4. С. 11-16.
- Черноусько Ф. Л. Эллипсоидальные аппроксимации множеств достижимости управляемых линейных систем с неопределенной матрицей//Прикладная математика и механика. 1996. Т. 60, № 6. С. 940-950.
- Куржанский А. Б., Фурасов Б. Д. Задачи гарантированной идентификации билинейных систем с дискретным временем//Известия Академии наук. Теория и системы управления. 2000. № 4. С. 5-12.
- Пацко Б. В., Пятко С. Г., Федотов А. А. Трехмерные множества достижимости нелинейных управляемых систем//Известия Академии наук. Теория и системы управления. 2003. № 3. С. 8-16.
- Кузьмин В. П., Ярошевский В. А. Оценка предельных отклонений фазовых координат динамической системы при случайных возмущениях. М.: Наука. Физматлит, 1995. 298 с.
- Розенвассер Е. Н., Юсупов Р. М. Чувствительность систем автоматического управления. Л.: Энергия, 1969. 208 с.
- Saltelli A., Andres Т. Н., Homma T. Sensitivity analysis of model output: An investigation of new techniques//Computational Statistics and Data Analysis. 1993. Vol. 15. P. 211-238.
- Li Shengtai, Petzold Linda. Software and algorithms for sensitivity analysis of large-scale differential algebraic systems//Journal of Computational and Applied Mathematics. 2000. № 125. Р. 131-145.
- Leis J., Kramer M. The simultaneous solution and sensitivity analysis of systems described by ordinary differential equations//ACM Transactions on Mathematical Software. 1988. Vol. 14, iss. 1. P. 45-60.
- Новиков В. А., Рогалев А. Н. Построение сходящихся верхних и нижних оценок решения систем обыкновенных дифференциальных уравнений//Журнал вычислительной математики и математической физики. 1993. Т. 33, № 2. С. 219-231.
- Рогалев А. Н. Использование границ глобальной ошибки в гарантированных оценках решений обыкновенных дифференциальных уравнений//Вычислительные технологии. 2002. T. 7, ч. 4. С. 88-95.
- Рогалев А. Н. Гарантированные методы решения систем обыкновенных дифференциальных уравнений на основе преобразования символьных формул//Вычислительные технологии. 2003. T. 8, № 5. С. 102-116.
- Рогалев А. Н. Включение множеств решений дифференциальных уравнений и гарантированные оценки глобальной ошибки//Вычислительные технологии. 2003. T. 8, № 6. С. 80-94.
- Rogalyov A. N. Computation of reachable sets guaranteed bounds//Proceedings of the IASTED International Conferences on Automation, Control, and Information Technology -Control, Diagnostics, and Automation (ACIT -CDA 2010). Calgary: ACTA Press, B6, 2010. P. 132-139.
- Рогалев А. Н. Гарантированные оценки и построение множеств достижимости для нелинейных управляемых систем//Вестник СибГАУ. 2010. 5(31). С. 148-154.
- Рогалев А. Н. Вычисление гарантированных границ множеств достижимости управляемых систем//Автометрия. 2011. T. 47, № 3. С. 100-112.
- Rogalev A. N. Calculation of Guaranteed Boundaries of Reachable Sets of Controlled Systems//Optoelectronics, Instrumentation and Data Processing. 2011. Vol. 47. № 3. P. 287-296.
- Рогалев А. Н., Рогалев А. А. Численный расчет включений фазовых состояний в задачах наблюдения за движением самолета//Вестник СибГАУ. 2012. 1(41). С. 53-57.
- Рогалев А. Н. Безопасность сложных систем и оценки областей допустимых отклонений//Современные технологии, системный анализ, моделирование. 2014. № 4 (44). С. 84-91.
- Белогородский С. Л. Автоматизация управления посадкой самолета. М.: Транспорт, 1972. 352 c.
- Буков В. Н. Адаптивные прогнозирующие системы управления полетом. М.: Наука, 1987. 232 c.
- Автоматизированное управление самолетами и вертолетами/С. М. Федоров . М.: Транспорт, 1977. 248 c.
- Гурман В. И., Квоков В. Н., Ухин М. Ю. Приближенные методы оптимизации управления летательным аппаратом//Автоматика и телемеханика. 2008. № 4. С. 191-200.


