Использование генетического алгоритма при выполнении диагностики
Автор: Баратов Ж.Р.
Журнал: Экономика и социум @ekonomika-socium
Рубрика: Основной раздел
Статья в выпуске: 3-1 (82), 2021 года.
Бесплатный доступ
Для обучения заданной структуре в первую очередь проводится первоначальная подготовка преподаваемых данных: их следует разбить на разделы, которые образуют репрезентативные классы.
Функция genfis2 fuzzy logic toolbox
Короткий адрес: https://sciup.org/140258869
IDR: 140258869
Текст научной статьи Использование генетического алгоритма при выполнении диагностики
Правила строятся на основе этих классов. Прямое обучение выполняется с использованием алгоритма распределения ошибок и представляется отдельно для каждой сети, которая реализует условия правила и делает вывод для по этапмы:
-
1- этап:
-
1.1. Подготовка набора обучающих данных в режиме двойного просмотра, где J обозначает объем выбора.
-
{x (t), d (t)} = {xi (t),...,Xn (t), d (t)}, t = 1,2,..., J.
-
1.2. Разобьем пространство входящих переменных на N и Rk классов. В результате сгенерирована N обучающая выборка ( x f ( t ), d ( t )), в ней
j
=
1,2,...,
Jk
,
Jk - R
k
k-
количество выборок, представляющих поле, а также
J
j
+
J
2 +
...
+
JN
=
J
. Как уже отмечалось, вывод о том, что n-мерное пространство разделено на N сфер ( N
-
1.3. Использование генетических алгоритмов в области разделения обучающих данных. В этом случае характерной чертой является определение нескольких многомерных реляционных функции.
Если на вход алгоритма поступает значение X. то d. = [ d ; (1) ,..., d^N ) ] T опорные сигналы подаются на выходной слой по следующему правилу:
d (k) Г1, если xе R, i 0, если x{ £ Rk,
Тогда, i = 1, 2, ..., Jk; k = 1,..., N. В качестве альтернативы указывается область, к которой принадлежит точка.
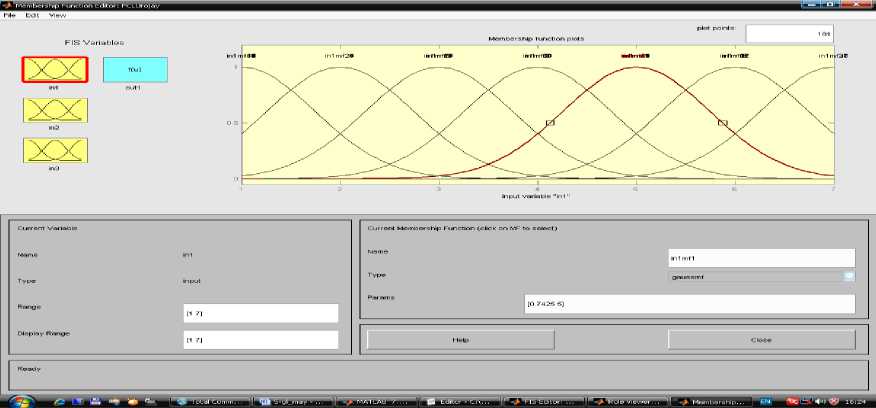
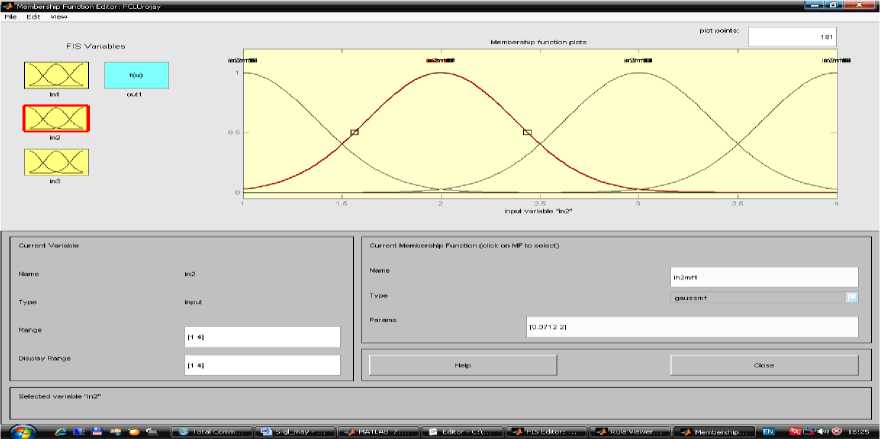
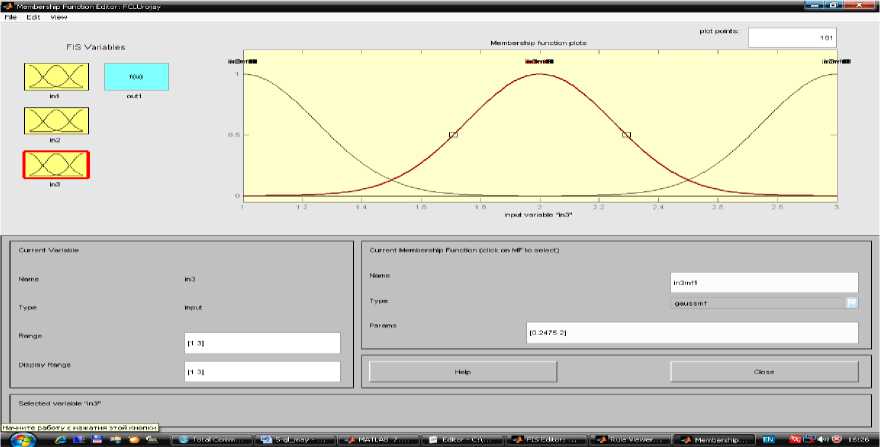
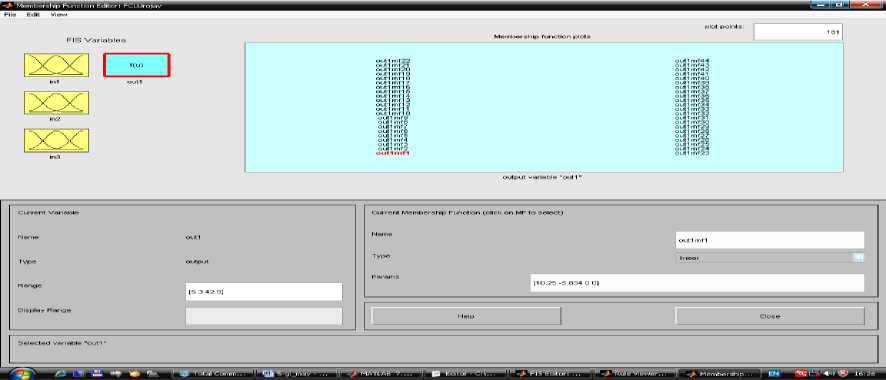
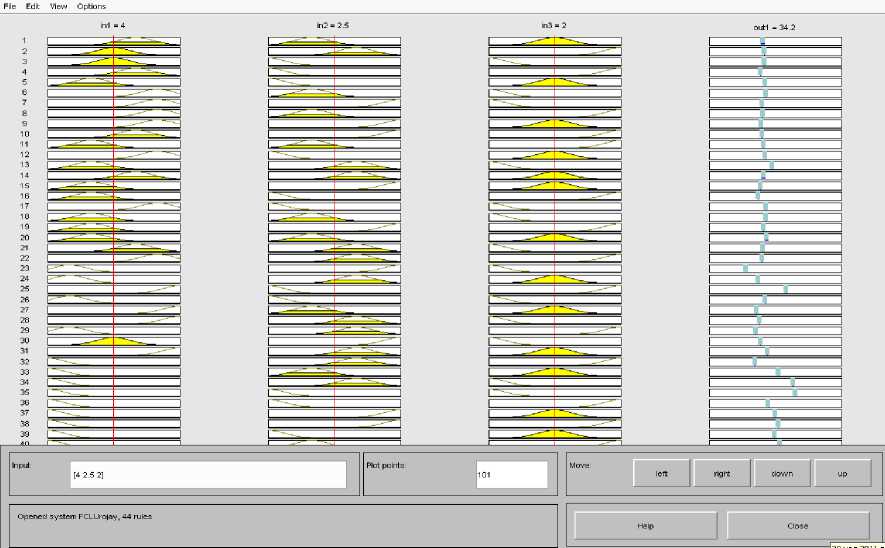
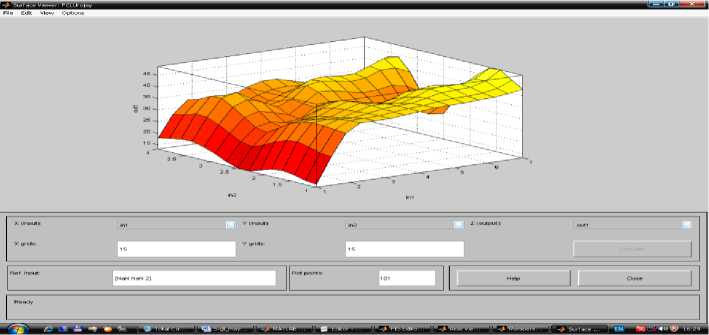
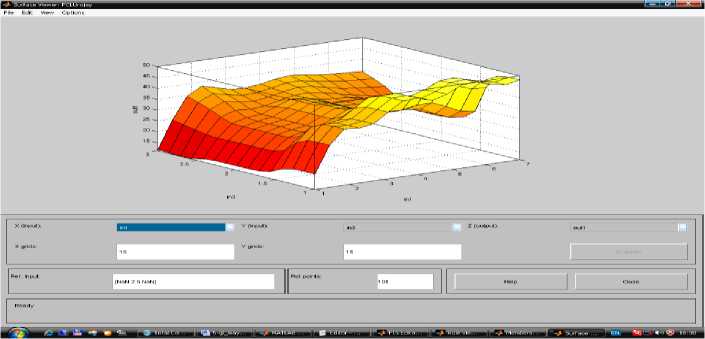
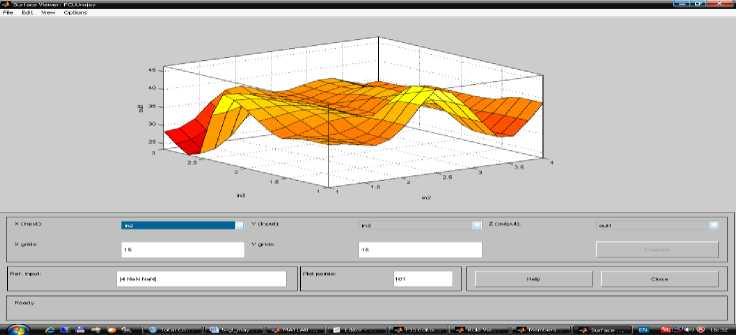
2-этап Использование генетического алгоритма в диагностических оценочных заключениях. Соответствует классу R {Xj,d В этом случае R(k) делает вывод для правила. Его результат прямо согласуется с k-правилом y(k) = f(k) (x1,..., xn ) будет бесспорным логическим завершением. Анализ результатов показывают, что в начальный момент времени точки зоны контакта движутся к оси симметрии, а затем от оси [7]. Выполнение описанных шагов и шагов гарантирует, что условия и выводы установлены для каждого правила. Этот набор правил формирует прочную базу знаний QXT (FIS). Функция genfis2 Fuzzy Logic Toolbox в системе Matlab используется для выполнения процесса синтеза модели типа Сугено. Синтезируемая фиксированная модель представляет собой логическую функцию, состоящую из трех входов и одного выхода. При вызове этой функции нужно указать «радиус» диагностики. В настоящий время инновации сложно приставит в неподготовленном для этого предварителен бизнесе. Поэтому сегодня мы рассмотрим некоторые трудности внедрения новых технологий в Узбекистане [13]. Сегодня современные компьютерные технологии активно внедряются во все сферы жизнедеятельности человека, в том числе в образовании [8]. Поскольку исходные данные диагностики находятся в единичном гиперкубе, значения радиуса должны находиться в диапазоне [0, 1]. Большие значения радиусов приводят к обнаружению всего нескольких кластеров и созданию компактной базы знаний. Однако при моделировании отношений некоторые особенности можно не учитывать. Фактических, синтез хорошей фиксированной базы знаний можно осуществить в диапазоне значений радиуса [0,2, 0,5]. Таким образом, было получено значение радиуса 0,3. горный метод вычитающей кластеризации, используемый функцией genfis2, позволяет быстро реализовать строгое правило на основе данных [40]. Реализацию нестабильной модели можно визуально наблюдать в FIS-Editor среды Matlab (рисунок 1). Рисунок-1. Модель нежеского подхода через FIS-Editor. Рисунок- 2. 1-Вариация входных данных в FIS-Editor Рисунок- 3. 2-Вариация исходных данных в FIS-Editor. Рисунок- 4. 3-Вариация исходных данных в FIS-Editor. Рисунок 5. Изменение выходных значений в зависимости от входа. Рисунок 6. Окно настройки и отображения базы правил. Можно будет настроить базу правил визуально и на показываеть результаты. Диагностическая задача, полученная для экспериментального исследования, включает 3 типа входных данных. Это также модель их индукции. Используя FIS-Editor, подробно описаны входные и выходные параметры[12]. Таким образом, при обработке изображений требуется по некоторым признакам выделять некоторые однородные области изображения. [11]. В работе выведены алгоритмы улучшения изображений, основанные на теории нечетких множеств. В данном разделе состояние вопроса обработки изображений с применением концепции нечетких множеств рассматривается применительно к следующим задачам: повышение качества изображений, сегментация изображений и выделение контуров на изображениях [6]. В столбцах 1, 2 и 3 на рисунке-7 показаны правила, генерируемые входящими данными. Изменяя их на определенную единицу, можно получить результаты с другим значением, т. е. Можно изменить значения типа почвы, типа удобрения и типов сортов. Соответственно, индекс производительности также варьируется в зависимости от данной модели. Рисунок 7. Трехмерное графическое представление результатов, полученных на основе 1-го и 2-го входных данных. Рисунок 8. 1 и 3 из входных данных трехмерное графическое представление результатов. Рисунок 9. Трехмерное графическое представление результатов, полученных на входах 2 и 3. На рисунках 7-9 показаны графики, показывающие результаты, основанные на взаимосвязи входных данных, соответственно.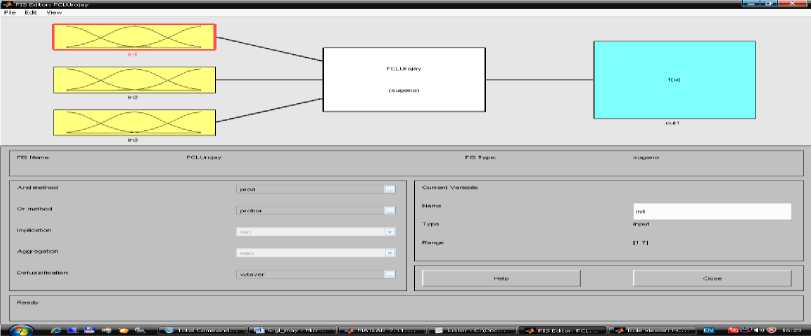
Список литературы Использование генетического алгоритма при выполнении диагностики
- Гонсалес Р., Вудс Р., Эддинс С. Цифровая обработка изображений в среде MATLAB. М.: Техносфера, 2006,-616 стр.
- Каршибоев Н. А., Тавбоев С. А. АЛГОРИТМЫ ВЫДЕЛЕНИЯ КОНТУРНЫХ ЛИНИЙ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ //EUROPEAN SCIENTIFIC CONFERENCE. - 2020. - С. 30-34.
- А.Савурбоев, Н.А.Дангалов, Г.М.Шертойлоқов, Ш.У.Эшонқулов Алгоритм расчета переходного процесса при ударе цилиндрического кольца о жесткое полупространствo. Молодой ученый, 246-250 2014 год.
- Эшонкулов Ш., Бурлиев А., Эшонкулова Ш. Научно-методический подход к созданию электронного учебника. - 2019. ГГТУ им. ПО Сухого
- Тавбоев С. А., Искандарова З. А. Обработка изображений с использованием теории нечетких множеств //Фундаментальные и прикладные исследования в современном мире. - 2019. - №. 27. - С. 42-45.
- ТАВБОЕВ С. А., КАРШИБОЕВ Н.А. МЕТОДЫ УЛУЧШЕНИЯ КОНТРАСТА ИЗОБРАЖЕНИЙ ПРИ НЕЧЕТКОЙ ИСХОДНОЙ ИНФОРМАЦИИ. ЗА ПУБЛИКАЦИЮ В МЕЖДУНАРАДНОМ НАУЧНО-ПРАКТИЧЕСКОМ ЖУРНАЛЕ. ЭКОНОМИКА И СОЦИУМ № 3(82) 2021
- Ибрагимова Н. А. МЕТОДЫ ОБРАБОТКИ ПОВЕРХНОСТИ ОБЪЕКТОВ ПОД УПРАВЛЕНИЕМ ЛАЗЕРНОГО ЛУЧА //Символ науки. - 2020. - №. 3.
- Хурамова Ф. У. ПРОБЛЕМЫ ВНЕДРЕНИЯ НОВЫХ ТЕХНОЛОГИЙ В УЗБЕКСТАНЕ //Матрица научного познания. - 2020. - №. 3. - С. 57-60.


