Использование гибридной модели на основе ВPNN-BC для диагностики рака молочной железы

Рак молочной железы остается одним из наиболее распространенных и опасных онкологических заболеваний, требующих высокоточных методов диагностики. В данной статье представлена инновационная гибридная модель, объединяющая прямую-обратную диффузионную нейронную сеть (BPNN) и байесовский классификатор (BC) для анализа данных Wisconsin Breast Cancer Dataset (WBCD).

Цель исследования – повышение точности дифференциации доброкачественных и злокачественных опухолей за счет синергии машинного обучения и статистических методов. Модель демонстрирует эффективность на всех этапах – от предобработки данных (нормализация, замена выбросов) до финальной классификации, достигая точности 94,6 % на тестовой выборке и 100 % – для сложных случаев. Результаты подтверждают потенциал гибридных систем искусственного интеллекта (далее – ИИ) для поддержки врачебных решений.

Процесс диагностики любого заболевания требует проведения необходимых лабораторных исследований, помогающих врачам в постановке диагноза. В некоторых случаях этот процесс прост, в других – сложен настолько, что у врача возникают сомнения в принятии решения. Поэтому для поддержки медицинских решений привлекаются компьютерные системы. Однако заболевание определяется набором факторов, указывающих на его наличие у пациента. Диагностика требует лабораторного анализа этих факторов, которые представляют собой числовые значения, отражающие состояние здоровья пациента. Эти значения формируют запись (record) с набором столбцов, соответствующих признакам заболевания (features). Каждой записи присваивается число, указывающее на наличие (0) или отсутствие (1) заболевания. Лабораторные данные группы пациентов образуют набор данных (dataset), к которому применяются вычислительные методы для поддержки медицинских решений в соответствии с мировыми стандартами.

Данные требуют предобработки перед использованием в моделях для улучшения производительности классификатора и сокращения времени обучения. Предварительная обработка включает:

• •    работу с пропущенными и аномальными данными;

• •    калибровку данных, которая преобразует исходные данные в более подходящий для классификатора формат [1].

Настоящее исследование направлено на поддержку принятия медицинских решений при диагностике некоторых заболеваний с использованием технологий ИИ и статистики

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление». 2025. № 3

с высокой точностью. Для достижения этой цели мы предлагаем и оцениваем различные модели этих технологий, стремясь использовать преимущества каждой из них для достижения максимальной точности обобщения. Предложенные модели были протестированы на наборе данных по раку молочной железы и наборе данных по диабету.

Исследования использовали различные технологии на наборе данных по раку молочной железы Университета Висконсина (Wisconsin Breast Cancer Data, WBCD). S.M. Kamruzzaman и Md. Monirul Islam [2] применили алгоритм извлечения правил из искусственных нейронных сетей (Rule Extraction from ANNs – REANN) для задач медицинской диагностики с целью извлечения правил, полезных для прогнозирования. Точность классификации их многослойного перцептрона (MLP) составила 96 %. Mohammad Sammany также провел исследование на том же наборе данных, используя нейронную сеть с десятью нейронами в скрытом слое и функцией активации Softmax на выходе, достигнув точности классификации 99,41 % [3]. Многочисленные исследования были проведены на наборе данных Pima Indian Diabetic Database (PIDD) для диагностики диабета. D. Michie c соавторами применили нейронную сеть с обратным распространением ошибки (backpropagation), достигнув точности классификации 75,2 % [4]. K.W. Wong и P. Jeatrakul [5] также применили нейронную сеть с обратным распространением ошибки, получив точность классификации 76,17 %. Ниже представлены модели, применяемые в данном исследовании.

Опухоли молочной железы являются наиболее распространёнными опухолями у женщин. Примерно 90 % из них – доброкачественные, 10 % – злокачественные. В Соединённых Штатах Америки ежегодно регистрируется около 180 тыс. новых случаев рака молочной железы, и происходит более 40 тыс. смертей, вызванных этим заболеванием. Статистические данные США указывают на то, что у одной из каждых 8–10 женщин в течение жизни разовьётся рак молочной железы. На Рисунке 1 представлен продольный разрез женской груди.

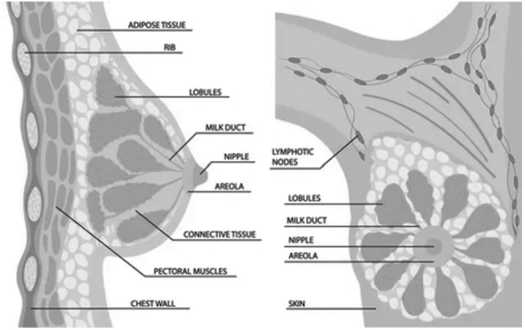
Рисунок 1. Продольный разрез женской груди Источник: [6].

Причины рака молочной железы:

• •    генетика, вирусы, питание, радиация, лекарства, гормоны;

• •    возраст, беременность после 30 лет, ранняя менструация (до 12 лет), менопауза после 50 лет, ожирение, семейная история рака.

Использование гибридной модели на основе ВPNN-BC для диагностики рака молочной железы

Симптомы рака молочной железы:

• •    безболезненное уплотнение в груди;

• •    выделения из соска (с кровью или без);

• •    изменение цвета кожи соска, трещины или втяжение;

• •    увеличение лимфоузлов в подмышечной области;

• •    локальная боль (редко при злокачественных опухолях).

Набор данных, применённый к предложенной модели, представляет собой базу данных пациентов с раком молочной железы (Wisconsin Breast Cancer Data – WBCD), официально признанную Университетом Висконсина (University of Wisconsin) и доступную по адресу:

Набор данных включает 699 наблюдений. Каждая запись содержит 9 атрибутов (признаков), выступающих в качестве входных данных для моделей машинного обучения. На основе этих признаков обученные модели способны прогнозировать состояние пациента (клинический исход) после обучения на подмножестве данного набора данных.

В Таблице 1 представлены признаки рака молочной железы с указанием имен переменных (названий признаков) и их областей определения. Значение 1 в столбце метки класса (Class) в наборе данных соответствует доброкачественному образованию (Benign), 0 – злокачественному (Malignant).

Таблица 1

Распределение образцов по типу опухоли

Данные / классификация	% от общего объёма данных
Доброкачественные	458 / 65,5
Злокачественные	241 / 34,5
Всего наблюдений	699

На Рисунке 2 представлена гибридная (предлагаемая) модель на основе прямой-об-ратной диффузионной сети и байесовского классификатора.

Модель начинается с предобработки набора данных (WBCD) для получения более релевантных данных.

Обработка выбросов выполняется по критерию D ( i ) - i >  2^ , где D ( i ) - значение признака; µ – медиана признака; σ – стандартное отклонение.

Аномальные значения заменяются медианой.

2( D ( i ) - min)

--1

max - min

Данные нормализуются в диапазон [-1,1] по формуле D(i) = где

D(i) - значение признака; min и max - минимальное и максимальное значение вектора признака соответственно. В результате этой предобработки данных мы получаем новый, более подходящий для модели набор данных, который был откалиброван [7].

Затем модель случайным образом разделяет данные на обучающий набор (Training Set – для обучения модели), набор проверки (Validation Set – для оценки ошибки обобщения: модель, достигающая наименьшей ошибки на наборе проверки, имеет лучшее обобщение на тестовых данных) и тестовый набор (Testing Set – для тестирования модели).

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление». 2025. № 3

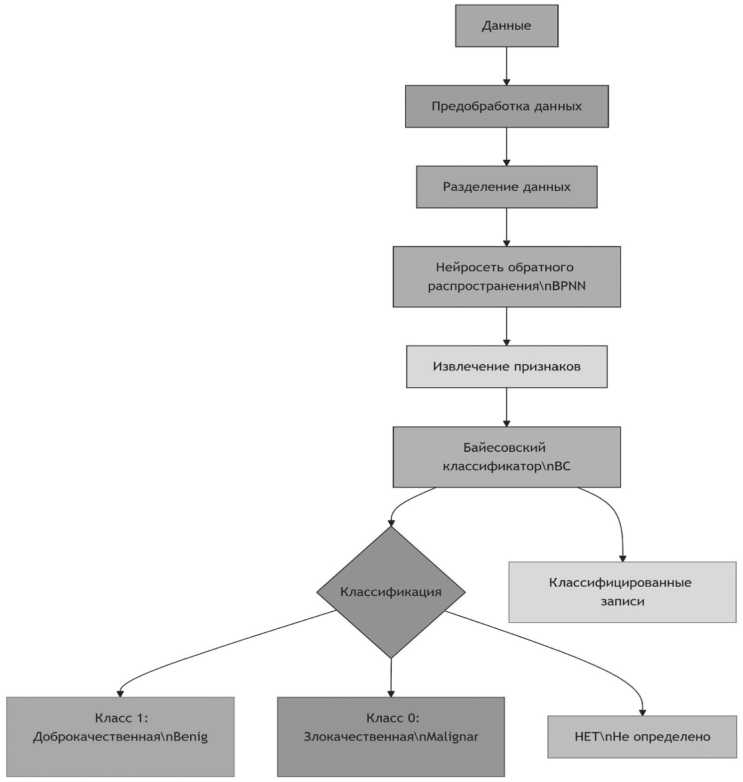
Рисунок 2. Схема гибридной модели НСРП-БК Источник: здесь и далее рисунки выполнены автором.

В Таблице 2 представлено количество обучающих, валидационных и тестовых образцов для доброкачественных и злокачественных случаев при применении модели.

Таблица 2

Количество обучающих и тестовых образцов для доброкачественных и злокачественных случаев

Данные / Классификация	Обучающие образцы	Валидационный набор (набор валидации)	Тестовые образцы	Всего наблюдений
Доброкачественные	326	70	62	458
Злокачественные	163	35	43	241
Всего наблюдений	489	105	105	699
% от общего объема данных	70	15	15	100

Источник: здесь и далее таблицы составлены автором.

Использование гибридной модели на основе ВPNN-BC для диагностики рака молочной железы

Модель начинает применять прямую-обратную диффузионную сеть. На Рисунке 3 показана сеть, применённая к набору данных в программе Matlab 2022.

Рисунок 3. Диффузионная сеть обратного распространения в модели

Сеть состоит из входного слоя с девятью входами (признаками), скрытого слоя из 5 нейронов с функцией активации гиперболического тангенса (биполярной сигмоидой) Hyperbolic Tangent Sigmoid и выходного слоя с одним нейроном с линейной функцией активации. Алгоритм обучения (тренировки) – алгоритм LM [8]. Максимальное количество эпох обучения – 1000. Также сетью использовались параметры, приведенные в Таблице 3.

На Рисунке 4 представлен график производительности сети на этапах обучения, валидации и тестирования. Результаты свидетельствуют о достижении наилучшей производительности на 8-й эпохе в соответствии с критерием среднеквадратической ошибки (Mean Square Error – MSE), значение которой на данной эпохе составило 0,037611.

Таблица 3

Основные параметры, используемые с сетью

Минимальный градиент производительности	min_ grad = 10 5
Максимальное количество ошибок валидации	max_ fail = 6
Параметр регулировки Марквардта	mu = 10 -3
Коэффициент уменьшения Марквардта	mu dec = 10 -2 ^^^~
Коэффициент увеличения Марквардта	mu inc = 10 ^^^~
Максимум Марквардта	mu max = 10 10 ^^^~

На графике наблюдается достижение минимума градиента на 13-й эпохе: Gradient = 5,5254106 ^-6

При этом значение параметра коррекции Марквардта (mu) на той же эпохе mu = 10 - 11 , тогда как в начале обучения mu = 10 - 3 . Значение параметра проверки валидации (valfail) на данной эпохе 0.

На Рисунке 6 представлена гистограмма ошибок для трёх этапов: обучение, валидация, тестирование. Ошибки рассчитываются на каждом этапе как разность между целевым и выходным значением.

Поскольку сеть не классифицировала все тестовые образцы на предыдущем этапе, модель обучает байесовский классификатор на немаркированных данных из фазы обучения

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление». 2025. № 3

сети для последующей классификации ранее неклассифицированных тестовых данных. В Таблице 4 представлено количество обучающих и тестовых образцов для доброкачественных и злокачественных случаев, не классифицированных на предыдущем этапе.

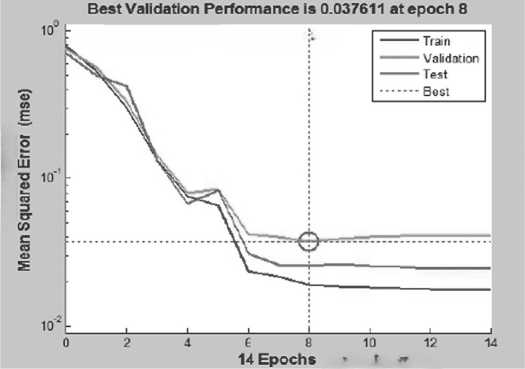
Рисунок 4. Наилучшая производительность сети была достигнута на 8-й эпохе На Рисунке 5 демонстрируется состояние сети в процессе обучения.

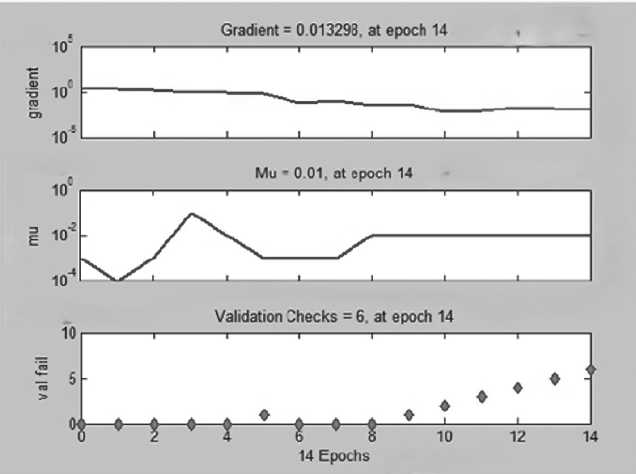
Рисунок 5. Состояние сети в процессе обучения

Использование гибридной модели на основе ВPNN-BC для диагностики рака молочной железы

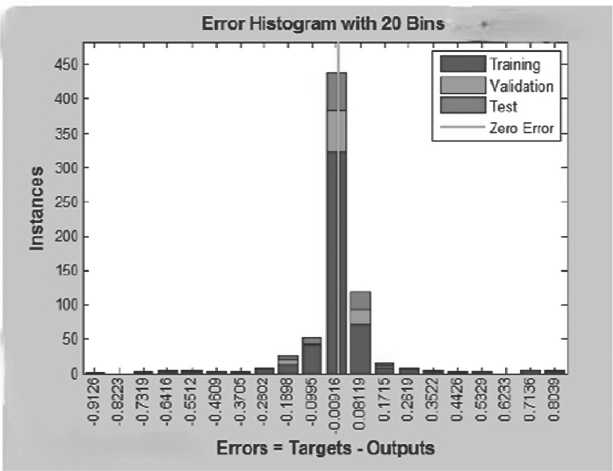
Рисунок 6. Гистограмма ошибок для трёх этапов

На Рисунке 7 представлен график регрессии выходных значений сети при тестировании. Коэффициент регрессии для тестовых данных составляет 0,97929.

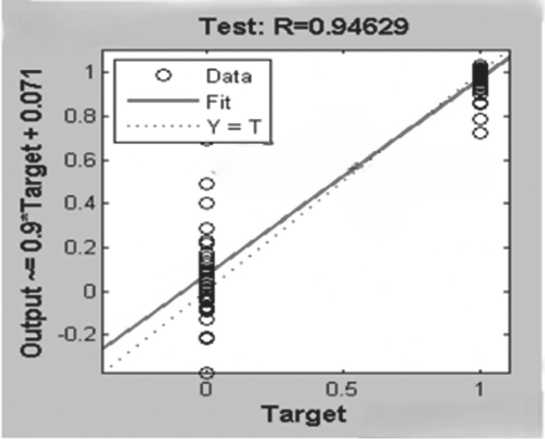
Рисунок 7. График регрессии тестовой выборки

Таблица 4

Количество обучающих и тестовых образцов для доброкачественных и злокачественных случаев

Данные / лассификация	Обучающие образцы	Валидационный набор (набор валидации)	Тестовые образцы	Всего наблюдений
Доброкачественные	8	2	1	11
Злокачественные	10	6	7	23
Всего наблюдений	18	8	8	34
% от общего объема данных	54	23	23	100

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление». 2025. № 3

Модель применяет байесовский классификатор к предыдущему набору данных. Модель прекращает работу, если корректно классифицирует весь предыдущий тестовый набор данных.

При применении модели с использованием ядерного распределения (Kernel

Distribution) была получена матрица неточностей (Confusion Matrix):

Точность классификатора вычисляется по формуле a 1 + a22

Accuracy =-------11----22------, all + a12 + a 21 + a 22

a₁₁ = 7 указывает количество записей класса 0, которые классифицируются как класс 0;

^а ₂₂ = 1 указывает количество записей класса 1, которые классифицируются как класс 1;

а ₁₂ = 0 указывает количество записей класса 0, которые классифицируются как тип 1;

а ₂₁ = 0 указывает количество записей класса 1, которые классифицируются как тип 0.

Подставляем в предыдущую формулу для вычисления точности байесовского класси- фикатора Accuracy =

7 + 1

7 + 0 + 0 + 1

цели, как показано в Таблице 5.

= 1 , в которой вектор выхода соответствует вектору

Таблица 5

Векторы цели и выхода после применения байесовского классификатора, что указывает на правильную классификацию всей предыдущей тестовой выборки

Целевой выходной	0	0	1	0	0	0	0	0
Фактический выходной	0	0	1	0	0	0	0	0

На Рисунке 8 показан график выходных данных байесовского классификатора BC, соответствующих векторам выхода и целевым значениям.

Рисунок 8. График производительности классификатора

Применение предложенной модели показало, что сеть BPNN успешно обобщила свои знания на тестовых данных из 105 записей (62 доброкачественных и 43 злокачественных случая), правильно классифицировав 94,629 % из них согласно критерию среднеквадратичной ошибки (СКО), которая на 8-й эпохе валидации составила 0,037611.

Использование гибридной модели на основе ВPNN-BC для диагностики рака молочной железы

В то же время BC продемонстрировал 100-процентную точность, корректно классифицировав все тестовые данные из 8 записей (1 доброкачественный и 7 злокачественных случаев), что подтверждается матрицей неточностей, выведенной классификатором.

Применение гибридной модели BPNN-BC подтвердило её эффективность в диагностике рака молочной железы. Комбинация нейронной сети (с точностью 94,6 % на 105 тестовых образцах) и байесовского классификатора (100-процентная точность для 8 сложных случаев) позволила минимизировать ошибки классификации. Ключевыми факторами успеха стали: предобработка данных (нормализация, замена выбросов медианой), оптимальное разделение выборки (70/15/15 %) и двухэтапная архитектура модели. Результаты превосходят традиционные методы (например, точность 75,2 % в [9]) и открывают перспективы для внедрения в клиническую практику.

Дальнейшие исследования могут быть направлены на адаптацию модели для диагностики диабета и других заболеваний с использованием аналогичных принципов.

Некоторые функции ядра [10–12]:

Линейное ядро	K I X i , X j ) = X i • X j
Гауссово ядро	—- —- 2 — ax. — x- e       i '
Экспоненциальное ядро	1                  1 K ( — * , X * ) = e "Y x i — x ' —- —>          —-   —> q
Полиномиальное ядро	K ( X^X j 1 = 1 p + X i X X ' ) — —2
Гибридное ядро	'      '                     -        - q -Y X i — X j K 1 X i , X j 1 = 1 p + X i X X j 1 e ' — -- -- --
Сигмоидальное ядро	K I X i , X j ) = tanh 1 kX{ x X j — 5 )