Использование имитационного моделирования в задачах управления распределенными запасами

По проведенным исследованиям в крупных машиностроительных организациях в запасах и в запасных частях для ремонта сложной техники, сосредоточены (и практически омертвлены) огромные денежные средства [1]. В наибольшей степени эта ситуация характерна для высокотехнологичных предприятий машиностроения, на которых эксплуатируется дорогостоящее оборудование с длительным жизненным циклом. Безусловно, это относится и к горному машиностроению, и к горнодобывающей отрасли.

Для решения проблем управления запчастями в конце прошлого века специалисты начали разрабатывать специальные математические модели, отражающие процессы расхода и восполнения запчастей, что в итоге позволило существенно (от 20 до 50%) сократить объёмы запасов и затраты на их приобретение и хранение при сохранении прежнего уровня эффективности и технической готовности систем.

Хотя проблема управления запасами имеет более широкий смысл (например, запасы сырья для производства или запасы товара для бесперебойной торговли), в настоящей статье она рассматривается только в контексте обеспечения техники запасными частями, необходимыми для поддержания ее работоспособности, то есть для проведения ремонтновосстановительных работ.

Проблема управления именно ремонтируемыми запчастями имеет важное значение, так как в высокотехнологичных отраслях машиностроения, где эксплуатируются дорогостоящие изделия, имеющие длительные жизненные циклы до 60% узлов являются ремонтируемыми Проведение ремонта оказывается экономически более выгодно, нежели закупка нового оборудования.

Для указанных отраслей обычно характерны следующие черты:

• •    Дорогостоящее оборудование с длительным жизненным циклом;

• •    Распределенная многоуровневая организация ремонтных и складских структур (обычно двухуровневая);

• •    Наличие многих типов запчастей, которые необходимо учитывать и контролировать;

• •    Первостепенное значение коэффициента готовности или доступности.

Для управления запасами в таких организациях на западе разработано целое семейство математических моделей, основанных на модели METRIC [1,2] (Multi Echelon Technique for Repairable Item Control) – модель для управления распределенными ремонтируемыми запасами Основные особенности этих моделей в том, что они исходят из системного подхода к задаче управления запасами. Это значит, что при расчете запасов учитывается влияние многих факторов друг на друга. Конечная цель при этом провозглашается как определение оптимальной зависимости коэффициента готовности от затрат, в каждой точке которой обеспечивается минимизация расходов при обеспечении заданного коэффициента готовности или максимизация коэффициента готовности при заданном уровне расходов.

Исходя из отмеченных выше характеристик систем управления запасами, задача создания математических моделей является крайне тяжелой, трудно формализуемой, со множеством ограничений. Поэтому помимо аналитических моделей важное значение имеет имитационное моделирование (ИМ). ИМ позволяет преодолеть многие указанные трудности.

В статье показано как используется разработанная в [3] имитационная модель двухуровневой СУЗ с пятью базами и депо, поддерживающими хранение и ремонт до четырех различных типов запчастей, для реализации алгоритма максимизации готовности парка конечных изделий (КИ) и определения затрат в этой системе. Модель построена на принципах математической модели METRIC и результаты моделирования показывают хорошее совпадение с аналитическими расчетами (отклонение в среднем до 5%).

Задача состоит в поиске оптимальной зависимости операционной готовности совокупности конечных изделий (например, группы станков в автоматизированном цехе) от затрат, связанных с закупкой и хранением запасных узлов. Под готовностью здесь понимается доля КИ, которая является готовой к использованию в любой момент времени.

K = (S o - S n )/S o (1)

где K – коэффициент готовности, S 0 – количество КИ в парке, S n – количество КИ, простаивающих по причине нехватки запасных частей.

Из предположения, что все узлы одинаково важны для функционирования КИ, следует, что дефицит любого узла приводит к простою КИ, а это, в свою очередь, приводит к уменьшению коэффициента готовности. Следовательно, оценкой эффективности управления запасом конкретного типа узлов может являться ожидаемое количества дефицитов PBO1 узла. Можно показать, что минимизация количества дефицитов приводит к максимизации коэффициента готовности.

Цель СУЗ – определение оптимальных уровней запасов по каждому типу узлов на каждой базе и в депо. Уровень запаса можно рассматривать как первоначально закупленное количество узлов каждого вида. Для рассматриваемых СУЗ в любой момент справедливо следующее уравнение баланса (все переменные являются неотрицательными случайными величинами):

s = OH + DI – BO (2)

где s – уровень запаса; OH – количества узлов в наличии; DI – количество узлов в ремонте или в доставке; BO – количество отложенных заказов (дефицитов).

Количество дефицитов может быть вычислено, зная информацию о количестве узлов, находящихся в ремонте. Если предположить, что в данный момент в ремонте находится s + k узлов, то из уравнения (2) следует, что имеется k дефицитов.

СУЗ является совокупностью нескольких логических блоков (рис. 1): блок входных данных; блок внешних воздействий; оптимизационный блок; блок управляемых переменных; блок выходных данных.

Входные данные представляют собой затраты на закупку и содержание запасов, либо входным может быть требование обеспечения необходимого коэффициента готовности (в данном случае для примера входом являются затраты). Внешним воздействием являются параметры потоков неисправностей узлов (характеристики надежности), время ремонта, время доставки и т.п. Управляемой величиной является уровень запаса на каждой базе и в депо по каждому типу запчастей. Выходом является значения среднего количества дефицитов по каждому узлу. В центре системы находится оптимизационный блок, который можно представить в виде черного ящика, на вход которого подаются входные данные и внешнее воздействие, внутри черного ящика вычисляется результирующая зависимая переменная.

Оптимизационный блок в процессе работы алгоритма выводит зависимость величины коэффициента готовности от затрат. Эта зависимость в каждой точке представляет собой решение конкретной задачи – количественное распределение запасных узлов каждого типа на каждой из баз и в депо, при котором достигается максимум готовности при данных расходах. Точки выше графика этой зависимости не достижимы, точки ниже графика дают худший результат.

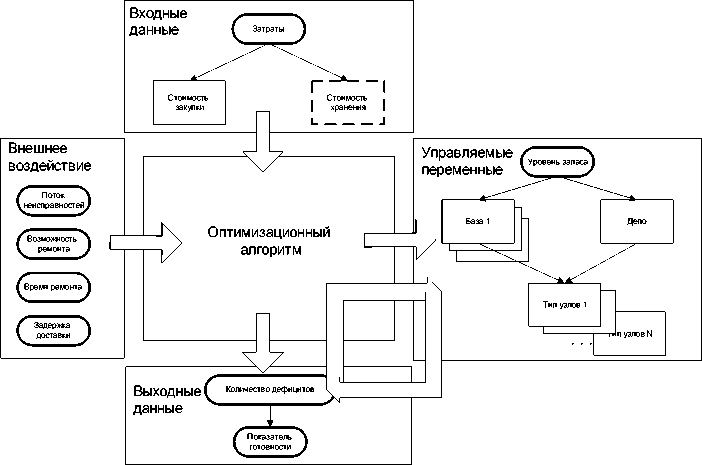
Рис. 1. Элементы схемы СУЗ.

Так как все внешние воздействия в общем случае являются случайными величинами, выходное значение количества дефицитов также является случайной величиной. Поэтому ядром оптимизационного алгоритма может быть имитационная модель, описанная в [2].

Оптимизационный алгоритм представляет собой реализацию граничного анализа [1, 3]. Суть граничного анализа состоит в том, он последовательно рассчитывает количество запчастей с учетом их типа и размещения по базам, начиная с отсутствия запаса как такового. На каждом шаге для определения узла, который добавляется в запас, необходимо анализировать изменение количества дефицитов при увеличении количества запаса только одну единицу для каждого типа узла Это граничное значение изменения количества дефицитов для каждого узла позволяет сделать выбор того узла, величину запаса которого предпочтительнее увеличить на единицу на данном шаге.

Как отмечалось выше, эффективность запаса конкретного узла оценивается количеством его дефицитов. Однако граничный анализ учитывает также стоимость узла, что позволят, при прочих равных условиях, отдавать предпочтение менее дорогим узлам. Непосредственно выбор проводится путем сравнения приращения эффективности на единицу затрат при добавлении очередной единицы данного узла в запас, которое для каждого типа узла выражается как уменьшение количества дефицитов, деленное на стоимость узла:

PBO(s_t - 1) - РВ0(,5^

где ∆ i – приращения эффективности на единицу затрат при добавлении очередной единицы узла i в запас; s i – уровень запаса; PBO(s i ) – ожидаемое количество дефицитов; c i – стоимость узла.

Оптимальность процедуры граничного анализа следует из того факта, что функция PBO(s) является выпуклой и монотонно убывающей. Поэтому каждая итерация граничного анализа обеспечивает поиск наилучшего варианта увеличения запаса на данном шаге, который при минимальных затратах приводит к максимальному уменьшению количества дефицитов в системе.

Для нахождения зависимости готовности от затрат в оптимизационном блоке СУЗ необходимо провести ряд экспериментов в соответствии с граничным алгоритмом. Блок схема реализации граничного алгоритма с использование имитационного моделирования приведена на рис. 2. На схеме используются следующие обозначения: ITEMS_LIMIT – максимальное количество запчастей в СУЗ; BASE_COUNT – количество баз в СУЗ; ITEM_COUNT – количество типов хранимых запчастей; ABO – фактическое суммарное количество дефицитов полученное в ходе имитационного моделирования на данном шаге алгоритма; Effect – приращение эффективности на данном шаге (∆).

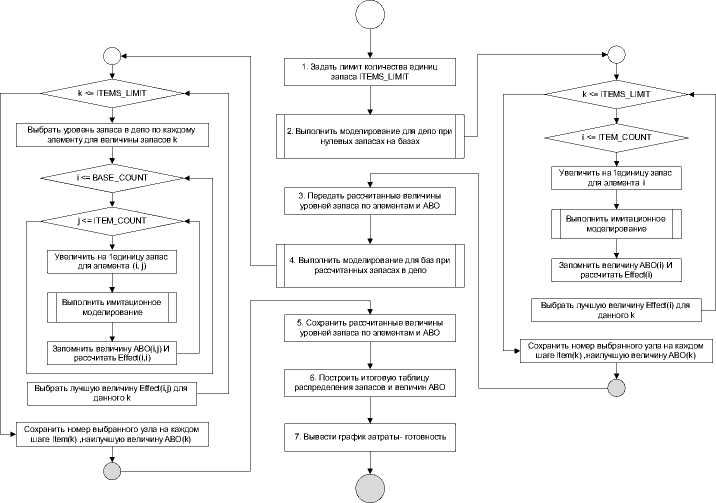
Рис. 2. Блок схема граничного алгоритма Параметры моделируемой СУЗ сведены в табл. 1 .

Параметры системы

Таблица 1

Параметры системы
Количество баз (BASE_COUNT), шт.		5
Количество типов узлов (ITEM_COUNT), шт.		4
Распределение потока заявок		Экспоненциальное
Распределение времени ремонта		Экспоненциальное
Вероятность ремонта на базе		20%
Параметр потока заявок, шт./год	Тип 1	23
	Тип 2	17
	Тип 3	20
	Тип 4	2
Стоимость единицы, тыс. у.е.	Тип 1	1
	Тип 2	1
	Тип 3	1
	Тип 4	1
Время ремонта на базе, лет	Тип 1	0.01
	Тип 2	0.015
	Тип 3	0.019
	Тип 4	0.1
Время ремонта в депо, лет	Тип 1	0.0253
	Тип 2	0.03
	Тип 3	0.035
	Тип 4	0.12
Время доставки из депо на базу, лет	База 1	0.01
	База 2	0.01
	База 3	0.01
	База 4	0.01
	База 5	0.01

Максимальное количество узлов в запасе устанавливается равным 20 единицам (ITEMS_LIMIT). Технические подробности шагов 2 – 5 алгоритма опущены.

Далее приведены результаты алгоритма – итоговая таблица (табл. 2, п. 6 алгоритма) и график зависимости готовность – затраты (рис. 3).

Следует отметить, что алгоритм заведомо учитывает и количество КИ, и количество баз, и количество типов запчастей и стоимость каждого типа запчастей. Количество КИ учитывается неявно, так как у каждой базы есть свой параметр потока заявок (поломок), который напрямую зависит от количества КИ, однако в формуле расчета коэффициента готовности это количество входит явно. Стоимость типов узлов может быть различной, и она явно влияет на расчеты граничного анализа. В итоге совокупность всех факторов и параметров приводят к определенному поведению ИМ, в результате чего в системе наблюдается определенное количество дефицитов и именно это значение количества дефицитов используется на каждом шаге граничного анализа.

Таблица 2

Итоговая таблица зависимости готовности от затрат

Всего	В депо	На базах	ABO	∆ ABO	Затраты	Готовность
0	0	0	11,48	0,00	0	0,79
1	1	0	10,55	0,94	1	0,80
2	2	0	9,64	0,91	2	0,82
3	3	0	8,74	0,89	3	0,8
4	4	0	7,88	0,87	4	0,85
16	11	5	2,53	0,25	16	0,95
17	8	9	2,29	0,24	17	0,95
18	8	10	2,03	0,26	18	0,96
19	8	11	1,77	0,26	19	0,97
20	8	12	1,51	0,26	20	0,97

С технической точки зрения, при увеличении количества типов узлов существенно возрастает время проведения одного эксперимента (моделирования), поэтому к ИМ предъявляется повышенное требование

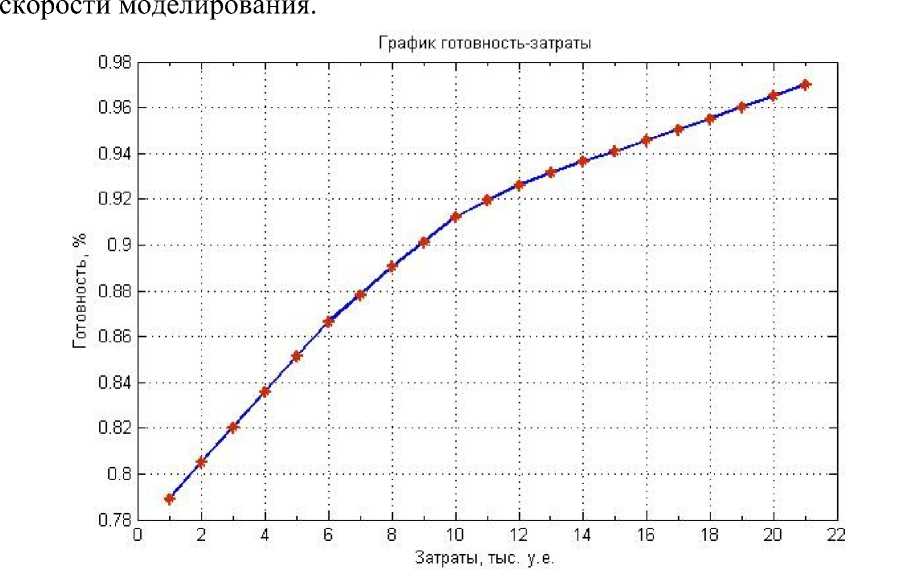
Рис. 3. Итоговая зависимость готовность

Выводы

• 1.    Для минимизации затрат на запасы и максимизации готовности парка конечных изделий разработана реализация граничного алгоритма, который использует имитационную модель в качестве основного элемента Имитационная модель отражает СУЗ, состоящую из пяти баз и депо, обслуживающих до четырех типов узлов.

• 2.    Алгоритм учитывает и позволяет задавать следующие характеристики СУЗ: стоимость каждого типа запасных узлов; параметры потока заявок отдельно по разным базам; количество КИ на разных базах.

• 3.    Построена зависимость операционной готовности парка конечных изделий от затрат на обеспечение должного уровня запчастей, по которой можно определить необходимые затраты для обеспечения соответствующего уровня готовности при наилучшем способе расхода средств.