Использование инфраструктуры облачных вычислений для моделирования сложных нанофотонных структур

Современные вычислительные задачи порождают всё более высокие требования к используемым методам параллельных вычислений и хранения данных [1, 2]. Разрабатываемые приложения должны эффективно работать на многоядерных и многопроцессорных вычислительных системах. Традиционным средством создания таких приложений является интерфейс MPI [3]. Применение MPI обеспечивает возможность разрабатывать гибкие приложения, которые детально учитывают особенности конкретного алгоритма программы и используемой вычислительной системы. Однако такая возможность MPI делает необходимой для разработчика реализацию многих низкоуровневых системных сервисов.

Технология реализации облачных вычислений MapReduce [4], по сравнению с MPI, позволяет повысить уровень абстракции, используемый при разработке параллельных приложений. MapReduce накладывает определённые ограничения на гибкость используемого алгоритма. Однако при этом MapReduce предоставляет простую модель программирования, распределённую файловую систему, механизм управления заданиями, средства администрирования вычислительной системы.

Моделирование прохождения электромагнитной волны видимого диапазона через многослойную структуру, включающую элементы рельефа размерами порядка длины волны падающего света, является ресурсоёмкой задачей [5 - 8]. Таким образом, её решение с помощью высокопроизводительных вычислительных средств – суперкомпьютера или кластера – становится оправданным.

Рассмотрим один из распространённых методов решения задач нанофотоники – метод Фурье-мод (Rigorous Coupled Wave Analysis – RCWA) [9 - 12], который может быть адаптирован к использованию технологии MapReduce. Для этого, в частности, ис- ходная задача, требующая больших вычислительных затрат (CPU-intensive), преобразована в задачу, требующую обработки больших объёмов данных (data-intensive).

В первом разделе статьи рассмотрены возможности технологии облачных вычислений MapReduce. Второй раздел статьи содержит описание потоков данных в методе Фурье-мод (RCWA). В третьем разделе статьи метод RCWA отображается на схему технологии MapReduce. Следующий раздел содержит результаты вычислительных экспериментов на Hadoop-кластере [13, 14], который является открытой реализацией технологии MapReduce. Выводы и направления дальнейшей работы приведены в заключительном разделе.

Описание технологии MapReduce

Технология MapReduce основана на том наблюдении, что многие задачи обработки информации обладают типовой базовой структурой [15-17]. Сначала в результате обработки большого объёма данных генерируются промежуточные результаты. Затем эти промежуточные результаты каким-то образом объединяются и систематизируются. Исходя из этого и в соответствии с принципами функционального программирования, MapReduce предоставляет разработчику более высокий, чем, например, MPI, уровень абстракции.

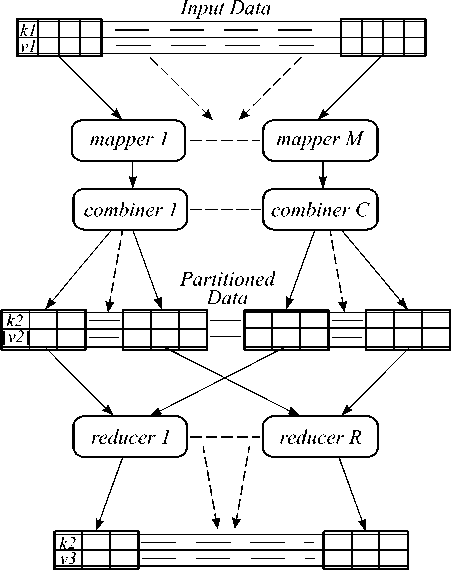
Разработчику в MapReduce достаточно реализовать две функции, чтобы получить работоспособное приложение. Во-первых, это функция map(), которая принимает на вход данные в формате ключ/значение (key/value) и генерирует промежуточные данные в таком же формате. Во-вторых, это функция reduce(), которая получает от функции map() на вход данные ключ/значение. Функция reduce() генерирует произвольное количество конечных пар ключ/значение, которые являются результатом обработки исходного массива данных. Эта двухэтапная схема показана на рис. 1.

Output Data

Рис. 1. Схема MapReduce

Среда исполнения MapReduce базируется на распределённой файловой системе [1] и контролирует процесс параллельного выполнения задания. Этот контроль включает в себя, например, координацию местоположения данных и кода, обработку ситуаций с отказом оборудования, а также сортировку и пересылку данных между вычислительными узлами перед началом этапа reduce.

MapReduce позволяет также использовать вспомогательную функцию combine(), которая аналогична функции reduce(), но получает на вход данные только от одной функции map(). Поэтому функция combine() задействована на каждом узле по отдельности и не может использовать промежуточные результаты на других узлах. Так как результаты работы функции map() должны быть в конечном итоге переданы с каждого вычислительного узла на несколько других вычислительных узлов, то функция combine() позволяет сократить объём промежуточных данных, которые пересылаются между вычислительными узлами. В том случае, если операции, реализуемые функциями map() и reduce(), являются одновременно и ассоциативными, и коммуникативными, содержимое функции combine() совпадает с содержимым функции reduce().

Промежуточные данные разделяются на части, количество которых равно количеству узлов, на которых выполняется функция reduce(). Разделение данных по умолчанию происходит путём расчёта значения hash-функции для каждого промежуточного ключа. Таким образом, на каждый из узлов, на которых выполняется функция reduce(), отсылается приблизительно одинаковый объём данных.

Идея разделения большой вычислительной задачи на подзадачи, параллельное выполнение этих подзадач и объединение результатов на заключительном этапе не является новой. Однако относительно недавно было продемонстрировано на практике, что такая схема позволяет освободить разработчика параллельных приложений от ряда сложностей использования современных высокопроизводительных вычислительных средств, при этом оставляя разработчику свободу в решении достаточно широкого круга задач. Реализация схемы MapReduce в виде фреймворка требует учёта многих аспектов использования распределённых вычислительных систем. Рассмотрим некоторые из них.

Во-первых , фреймворк должен обеспечивать балансировку загрузки вычислительных узлов системы. Балансировку загрузки в MapReduce выполняет один из узлов – master – на который копируется экземпляр кода программы. Узел master распределяет подзадачи map и reduce по рабочим узлам – workers. Каждый раз, когда рабочий узел освобождается, узел master назначает для него новую подзадачу – map или reduce.

Во-вторых , должна обеспечиваться отказоустойчивость работы вычислительной системы. Используя распределённые системы, содержащие сотни и тысячи компьютеров, постоянно приходится иметь дело с отказами вычислительных узлов. Чтобы определить проблемный узел, узел master периодически опрашивает рабочие узлы и формирует список отказов, который учитывается при распределении подзадач по узлам.

В-третьих , необходимо обеспечить близость данных и вычислений, чтобы сократить пересылку данных между узлами. Поэтому важно учитывать, какие данные уже находятся на узлах, и в соответствии с этим распределять вычислительные подзадачи. В реализациях MapReduce это достигается использованием специальной файловой системы. В этой распределённой файловой системе каждый файл разделяется на блоки – например, по 64 МБ. Несколько копий этих блоков хранятся на различных узлах. Благодаря такому механизму репликации данных узел master имеет выбор при распределении подзадач по узлам. В случае отказа одного из узлов выполнявшаяся на нём подзадача будет перенаправлена на другой узел, который содержит необходимые данные. Таким образом, данные, как правило, считываются локально и не загружают сеть между узлами.

Потоки данных в методе RCWA

Моделирование прохождения света через структуру, включающую элементы рельефа размером порядка длины волны падающего света, требует решения уравнений Максвелла [18]. Как правило, для этого используют один из разработанных численных методов. В данной статье рассмотрен метод RCWA.

Постановка задачи представлена на рис. 2. Пространство разбито на три области. Во-первых, однородная область I с диэлектрической проницаемо- стью 81, в которой распространяются падающая и отражённая электромагнитные световые волны. Во-вторых, неоднородная область II, которая включает исследуемую наноструктуру с периодической модуляцией диэлектрической проницаемости. В-третьих, однородная область III с диэлектрической проницаемостью 83, в которой распространяется прошедшая волна.

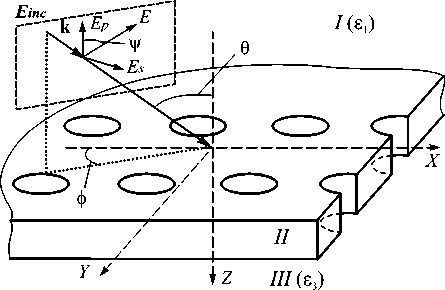
Рис. 2. Анализируемая наноструктура

На структуру падает линейно поляризованная монохроматическая плоская волна с волновым числом k 0 = 2 л/% 0 :

E inc = ¹ e exp [ ^- j ^k inc i r ] .

Величины 6 и ф определяют, соответственно, меридиональный и азимутальный углы падения света. Плоскость поляризации падающей плоской волны задаётся величиной у . Таким образом, k inc = k0 4^1 Х

x ( sin 6 cos ф 1 x + sin 6 sin ф 1 y + cos 6 1 z ) =

= k. 1 + k.   1 + k.   1 , inc,x x inc, y y inc,z z , где

1 e = ( cos у cos 6 cos ф- sin у sin ф ) 1 x +

+ ( cos у cos 6 cos ф- sin у cos ф ) 1 y -

• - cos у sin 6 1 z .

Периодическая двумерная геометрическая структура описывается выражением

• e ( x , y , z ) = e ( x + nd x , y + md y , z ).                 (2)

Метод RCWA предполагает разложение функции (2) в ряд Фурье.

• ^£ ( ^x , У ) = S ^e mn exp ( j K mn • ^r ) ,                    ⁽³⁾

m,n где

Km „= mKx 1 + nK 1 mn x x y y

и

K = 2 n / d_x , K = 2 n / d _v. x    xy    y

Количество членов ряда Фурье (3) задаёт количество рассчитываемых дифракционных порядков.

Чтобы рассчитать прохождение электромагнитной волны видимого диапазона света через наноструктуру, необходимо решить уравнения Максвелла. В методе RCWA анализируемая структура разбивается на слои, однородные в вертикальном направлении. В каждом из этих слоёв электромагнитное поле раскладывается в ряд Фурье, затем эти поля сшиваются на границах слоёв. В процессе расчётов для каждого слоя решается задача на собственные значения. Размер этой задачи определяет количество рассчитываемых дифракционных порядков. Рассмотрим случай конической дифракции на двумерной структуре. Положим, что количество учитываемых положительных дифракционных порядков для каждой из координат равно N. Тогда размер матрицы задачи на собствен- 4

ные значения равен ( 2 N + 1 ) . Эта матрица не зависит от толщины слоя. После решения задачи на собственные значения формируется система линейных уравнений. Решение этой системы позволяет получить оценки энергетической эффективности рассчитываемых дифракционных порядков.

Отметим, что при большом количестве рассчитываемых дифракционных порядков необходимо контролировать систематическую вычислительную погрешность.

Отображение метода RCWA на схему MapReduce

Рассмотрим использование метода RCWA для моделирования или оптимизации нанофотонных структур. В качестве примера такой структуры возьмём периодическую двумерную сетку, в каждом узле которой находится усечённый конус, изображённый на рис. 3 а . Пусть допустимые значения верхнего и нижнего радиусов усечённого конуса определяются, соответственно, верхней и нижней сторонами серого прямоугольника на рисунке. Количество допустимых значений каждого из радиусов определяется шагом дискретизации и равно W . Для применения метода RCWA требуется разбить анализируемую структуру на однородные слои в вертикальном направлении. Пусть количество этих слоёв фиксировано и равно L .

Как было сказано в предыдущем пункте, для каждого однородного слоя рассчитываются собственные значения и собственные вектора соответствующей матрицы. Рассчитанные значения не зависят от толщины однородного слоя. Без сохранения промежуточных результатов эта ресурсозатратная задача на нахождение собственных значений будет повторяться многократно. На рис. 3б показана зависимость количества задач NL на нахождение собственных значений и векторов от количества NW наборов значений верхнего и нижнего радиусов усечённого конуса без сохранения промежуточной информации (ступенчатый пилообразный график). Значения параметров L и W на рисунке положены равными 7 и 8, соответственно. Отметим, что количество задач на нахождение собственных значений и векторов, которые необходимо решить при сохранении промежуточной информации, равно W.

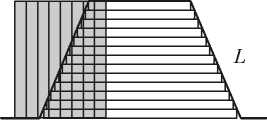
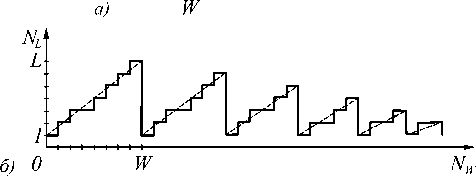
Рис. 3. Пример анализа двумерной дифракционной решётки: период решетки; допустимые значения верхнего и нижнего радиусов усечённого конуса выделены серым прямоугольником (а); количество задач на нахождение собственных значений и векторов, которые необходимо решить для каждого набора значений верхнего и нижнего радиусов усечённого конуса без сохранения промежуточной информации (б)

Сохранение промежуточной информации в данном случае преобразует изначально вычислительно затратную задачу в задачу, требующую интенсивного использования данных. Оценим количество памяти, которое потребуется для сохранения промежуточной информации.

Структура и количество входных параметров для моделирования нанофотонной структуры зависит, в частности, от типа структуры и целей моделирования. Можно выделить две основные группы входных параметров. Во-первых, параметры, описывающие геометрию структуры и её вариации. Во-вторых, параметры, задающие условия освещения данной структуры.

Оценим возможное количество входных параметров для моделирования нанофотонной структуры, период которой изображён на рис. 3 а . Начнём с группы геометрических параметров. Пусть количество допустимых значений ширины усечённого конуса равно 100 ( W = 100). Пусть также допускается вариация периода структуры. Количество допустимых периодов также равно 10. Переходим к группе параметров освещения. Пусть в нашем случае эта группа содержит три параметра. Во-первых, это длина волны падающего света. Во-вторых, это меридиональный угол падения. В-третьих, это азимутальный угол падения. Для каждого из трёх параметров также положим количество возможных вариаций равным 10. Таким образом, количество задач на нахождение собственных значений, промежуточные результаты которых необходимо сохранить, равно произведению вариаций описанных пяти параметров, т.е. 10⁶.

Оценим теперь размер сохраняемых промежуточных результатов. Эта величина зависит от количества рассчитываемых дифракционных порядков. Будем считать, что вычисления выполняются с ис- пользованием типа long double размером 16 байт, чтобы обеспечить высокую точность расчётов. На рис. 4а изображена зависимость размера сохраняемых данных от количества рассчитываемых дифракционных порядков. На рис. 4б показан совокупный объём хранимых промежуточных данных для различных комбинаций количества рассчитываемых дифракционных порядков и варьируемых параметров. Из рисунка видно, что объём данных может превышать 1 ТБ. Это позволяет отнести рассматриваемую задачу к классу data-затратных. Чтобы уменьшить размер хранимых промежуточных данных, можно использовать процедуру упаковки. Однако это, в свою очередь, влечёт соответствующие накладные расходы.

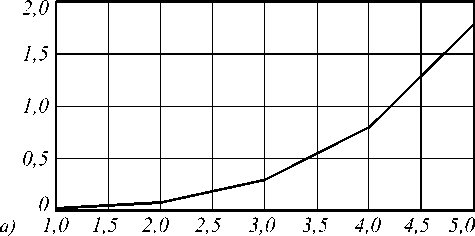
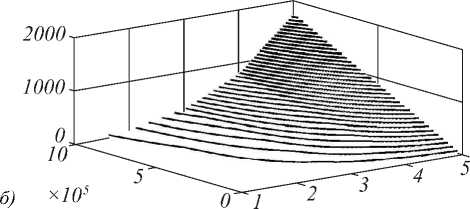
Рис. 4. Размер промежуточных данных

Перейдём непосредственно к процедуре отображения метода Фурье-мод на схему MapReduce. Определим структуру данных в хранилище промежуточных результатов. Для технологии MapReduce эта структура определяется парой «ключ/значение». Ключом для рассматриваемой задачи является совокупность геометрических параметров вертикального слоя структуры (без учёта толщины) и параметров, задающих освещение. Следующее соотношение является примером описания такой совокупности параметров.

K 1 = { d x , m x , b x , n x , d y , m y , b y , n y , ^ , 9 , Ф ] .

Здесь dx ,dy – периоды двумерной структуры bx , by – размер горизонтальных неоднородностей в слое; mx,my – количество этих неоднородностей; nx , ny – индекс рефракции этих неоднородностей. Последние три параметра описывают условия освещения.

Значением в рассматриваемой паре являются рассчитанные собственные значения и собственные вектора для одного слоя

• V = V 2 = { Eig } .

На рис. 5 изображена блок-схема метода RCWA в терминах технологии MapReduce. Функция Map получает на вход описание анализируемой структуры в виде ключа K ₂ . Данный ключ состоит из набора ключей K ₁ , которые задают слои структуры, а также из вектора t , который описывает толщины этих слоёв

K 2 = K 3 = { K 1 , t } .

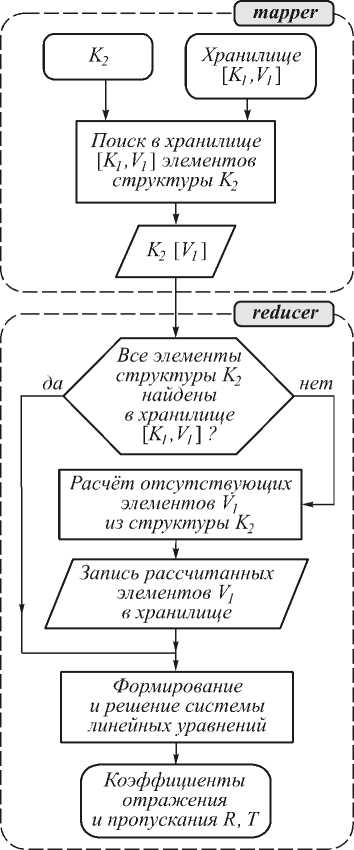
Рис. 5. Блок-схема метода RCWA, реализованного для технологии MapReduce

Далее функция Map по ключу K ₂ выполняет поиск промежуточных данных в хранилище. Таким образом, выходными данными функции Map являются пары K ₂ /[ V ₂ ]. Т.е. каждой структуре ставятся в соответствие промежуточные данные о слоях. Этот список промежуточных данных может содержать пустые величины, если необходимая промежуточная информация не находится в хранилище.

Найденные пары K ₂ /[ V ₂ ] являются входными параметрами функции Reduce. Данная функция рассчитывает недостающие промежуточные данные, записывает их в хранилище, затем формирует систему линейных уравнений и решает её.

В данной работе будем считать, что выходным параметром является дифракционная эффективность рассчитываемых порядков. Однако приводимые рассуждения верны и для других выходных параметров, например, для распределения электромагнитного поля в так называемой ближней зоне [18]. Таким образом, в рассматриваемой задаче

• V 3 = { R , T } .

Здесь R , T – энергетическая эффективность дифракционных порядков, соответственно, отражения и пропускания.

Результаты вычислительных экспериментов на Hadoop-кластере

Вычислительные эксперименты выполнялись на сравнительно небольшом Hadoop-кластере, состоящем из четырёх узлов. Каждый узел кластера содержал CPU Intel Xeon 2,13 GHz и RAM 4 GB.

На одном из узлов был запущен namenode-сервер, на другом – jobtracker-сервер. Оставшиеся два узла кластера использовались в качестве рабочих узлов. На каждом из рабочих узлов одновременно могло выполняться по два mapper и по два reducer, что соответствует параметрам, которые установлены по умолчанию. Остальные параметры hadoop-кластера также были равны значениям, принятым по умолчанию. В эксперименте измерялись скорости параллельного чтения из файловой системы HDFS и параллельной записи в эту файловую систему.

Усреднённое по выборке экспериментов значение скорости параллельного чтения составило r =460 мБ/с. Здесь и далее аббревиатура мБ означает «мегабайт». Скорость записи оказалась равна w =60 мБ/с. Задача оптимизации данных значений путём выбора соответствующих настроек кластера и параметров вычислительной задачи в данной работе не ставилась. Поэтому вышеприведённые величины r и w считаются фиксированными.

Оценим целесообразность предложенной схемы реализации метода RCWA. Для этого сравним время расчёта в соответствии с традиционным алгоритмом со временем расчёта по предложенной схеме. Основное время при расчёте по методу RCWA затрачивается на вычисление собственных векторов матриц, которые соответствуют слоям моделируемой наноструктуры.

Язык программирования java наиболее удобен для реализации гибких приложений в рамках программного пакета Hadoop. Поэтому на java был реализован алгоритм нахождения собственных векторов комплексной матрицы общего вида.

На рис. 6 показана зависимость времени расчёта собственных векторов матрицы от количества учи- тываемых положительных дифракционных порядков для одной координаты. Здесь предполагается,

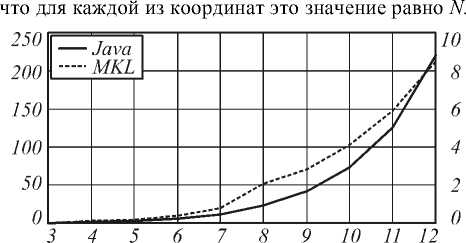
Рис. 6. Зависимость времени расчёта собственных векторов матрицы от N для java-реализации расчёта собственных векторов и реализации с использованием пакета Intel MKL

Левая ось Y на графике, изображённом на рис. 6, соответствует результатам работы java-приложения. Для сравнения правая ось Y этого же графика содержит результаты, которые были получены с помощью пакета Intel MKL.

Определим следующие параметры:

s – размер загружаемого файла (МБ), который обрабатывается одним mapper;

f – доля загруженного файла, которая используется mapper для нахождения собственных векторов (нормированная величина);

m – усреднённое количество использований одной матрицы из загруженного файла;

a ( N ) - размер матрицы слоя (МБ), в которой содержатся вычисленные собственные вектора;

е ( N ) - время вычисления собственных векторов для одной матрицы слоя структуры (с);

L – общее количество слоёв во всех структурах, которые обрабатываются одним mapper.

Тогда условие целесообразности использования предложенной схемы расчёта можно записать в следующем виде: время расчёта собственных векторов для всех анализируемых одним mapper структур (L • е) должно быть больше времени, которое затрачивается на: (1) чтение из HDFS файла размера s, (2) расчёт не найденных в этом файле собственных векторов анализируемых структур, (3) запись рассчитанных собственных векторов в HDFS.

Описанное выше условие можно представить в виде линейной зависимости величины L от коэффициента совокупного использования загруженного файла f • m :

( f • m ) > k • L + p ,                                (4)

где k (N ) =

a ² ( N )

5 (e (N )• w - a (N)) ’

P ( ^N ) =

a ( N ) • w

r (e (N )• w - a (N))

На рис. 7 заштрихована зона, для которой соотношение (4) выполняется. Наклон прямой k на рис. 7 определяет скорость, с которой должен расти коэффициент совокупного использования загруженного файла при возрастании L .

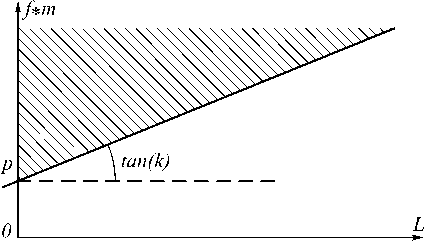
Рис. 7. Зависимость величины L от коэффициента совокупного использования загруженного файла f • m ;

заштрихована зона, для которой выполняется соотношение (4)

На рис. 8 показана зависимость k от количества учитываемых дифракционных порядков N при использовании программной реализации на языке java (а) и реализации с использованием пакета Intel MKL (б).

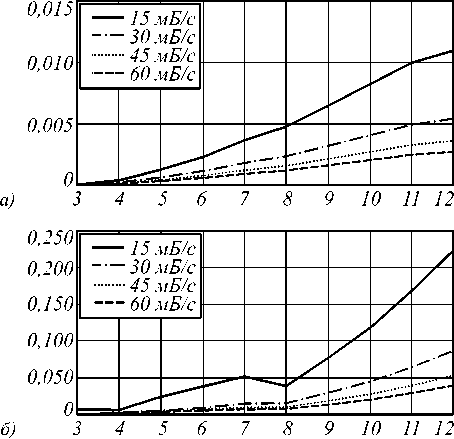
Рис. 8. Зависимость k от количества учитываемых дифракционных порядков N при использовании программной реализации на языке java (а) и реализации с использованием пакета Intel MKL (б)

На рис. 8 а видно, что наклон прямой из соотношения (4) очень мал. Таким образом, при использовании относительно медленной java-реализации расчёта собственных векторов нет необходимости стремиться существенно увеличивать коэффициент совокупного использования загруженного файла, чтобы остаться в рамках целесообразности предлагаемого подхода. Для быстрой MKL-реализации (рис. 8 б ) такая необходимость появляется. В этом случае могут быть рассмотрены различные варианты использования мета-данных.

Заключение

В работе рассмотрены вычислительные проблемы, возникающие при моделировании и оптимизации сложных нанофотонных структур методом Фурье-мод (RCWA). Предложено использование инфраструктуры облачных вычислений для решения этих проблем. Такой подход позволяет эффективно задействовать потенциал современных вычислительных средств для улучшения масштабируемости решаемой вычислительной задачи и повышения отказоустойчивости используемой вычислительной системы, что открывает новые возможности в решении задач дифракционной нанофотоники [19 - 21], магнитооптики [22 - 23] и плаз-моники [24- 25].

Работа выполнена при поддержке программы фундаментальных исследований Президиума РАН «Проблемы создания национальной научной распределительной информационно-вычислительной среды на основе развития GRID технологий и современных телекоммуникационных сетей», гранта Президента РФ поддержки ведущих научных школ № НШ-7414.2010.2 и грантов РФФИ № 10-07-00553, № 11-07-00153.