Использование интегрированной среды динамического моделированния OmegaLand для исследования характеристик регуляторов

Методология компьютерного моделирования

Научное познание – это особый род деятельности человека, направленный на постижение истинных знаний о мире, которые постоянно углубляются, совершенствуются и проверяются эмпирически, и достоверность которых обосновывается научно. Еще Эйнштейн писал: «То, что мы называем наукой, имеет своей исключительной задачей твердо установить то, что есть». Можно сказать, что основной задачей является дать истинное отражение текущих процессов и получение объективной картины того, что есть. Известным способом в научном познании является метод аналогии, который является исходным при разработке одного из самых мощных инструментов анализа и познания сложных технологических процессов – компьютерного моделирования. Сущность метода компьютерного моделирования заключается в замене технологического объекта математической моделью, что позволяет ученому исследовать объект в тех случаях, когда делать это на существующем объекте затруднительно или нецелесообразно, например, создание аварийных ситуаций или исследование свойств объекта при неэффективной загрузке. В то же время компьютерные модели позволяют проводить вычислительные эксперименты и оптимизировать работу сложных технологических процессов.

Таким образом, процесс компьютерного моделирования включает и построение модели, и ее апробацию для решения поставленной задачи: сбора данных, анализа, исследования, оптимизации или проектирования технологических процессов и оборудования. Поставленные задачи очень трудоемки и включают в себя огромное число элементов, переменных, параметров, условий и т. д. Построение точной модели занимает большое количество времени, так как требует включения всех элементов, учета мельчайших фактов и установления взаимосвязи между ними.

Для упрощения создания математической модели в интегрированной среде для динамического моделирования OmegaLand [ 1 ] , которая включает в себя динамический тренажер установки Visual Modeler, этап ее построения разбивается на части. На первом этапе строится «эквивалент» технологического объекта и связывание аппаратов и приборов информационными линиями. Далее математическая модель исследуется теоретическими методами и производится отладка модели, что позволяет получить важные предварительные знания об объекте.

Второй этап связан с созданием детальной математической модели. Далее подробнее рассматривается каждый из этапов построения модели для исследования динамических характеристик регуляторов уровня, давления и температуры [ 2 ] .

Выбор математических моделей и создание начальной модели

Программа Visual Modeler изначально содержит в себе большое количество математических моделей. Если какого-нибудь специфического аппарата нет в списке, то имеется возможность сделать для нее математическую модель и добавить в инструментарий. Исходя из принципиальной схемы, выбираем математические модели, которые в полной мере будут описывать данное оборудование. Добавление моделей в среде Visual Modeler сводится к перетаскиванию пиктограммы требуемой модели на рабочую область. Для упрощения отладки и ускорения создания модели процесса вначале создаем упрощенную математическую модель. В упрощенной модели не учитываются некоторые параметры аппаратов. После добавления модели в рабочую область программа попросит задать начальные настройки модели, к которым относятся название аппарата, выбор дополнительных методов расчета. Данное окно представлено на рис. 1.

Конфигурирование математической модели

После добавления моделей на рабочую область необходимо задать основные параметры моделей. Этими параметрами являются геометрические размеры оборудования, коэффициенты мас-сопередачи, теплопередачи и т. д. Окно настройки моделей представлено на рис. 2.

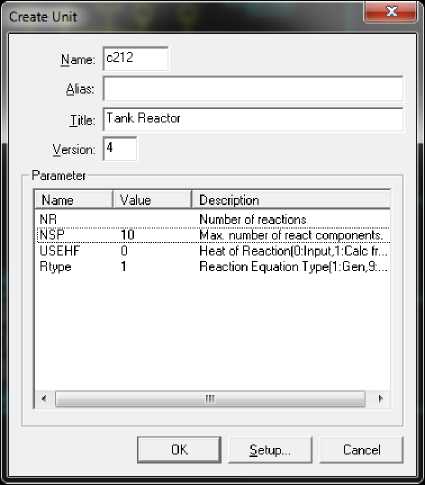
Рис. 1. Окно создания модели аппарата

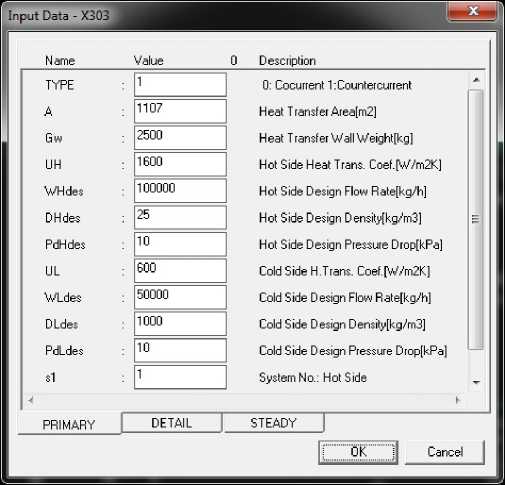
Рис. 2. Окно настройки модели

В окне настройки модели (см. рис. 2) содержатся 3 вкладки, которые имеют следующие значения:

PRIMARY – здесь содержатся наиболее важные параметры модели, которые существенно влияют на его поведение;

DETAIL – здесь содержатся дополнительные параметры модели, которые отвечают за дополнительные функции и использование которых необязательно, также здесь находятся параметры, позволяющие более тонко настроить модель;

STEADY – на данной вкладке находятся параметры, необходимые для расчета стационара объекта.

Данные параметры берутся из исходной проектной документации, а также из лабораторных опытов и экспериментов.

Также необходимо связать аппараты потоками. Для этого необходимо щелкнуть мышкой на выход аппарата и указать на вход следующего за ним. После этого программа предложит выбрать фазовое состояние потока и его название [ 3 ] . Окно настройки потока представлено на рис. 3.

При настройке регуляторов и датчиков необходимо нажать на вход датчика и указать, откуда берутся данные (с потока или аппарата). После этого программа предложит выбрать, какой именно параметр в потоке или аппарате необходимо использовать. Окно выбора параметра приведено на рис. 4.

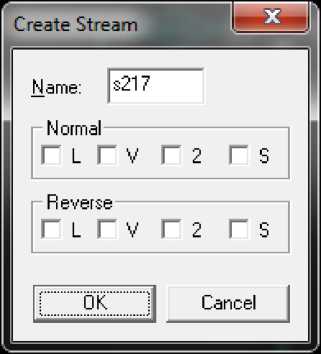
Рис. 3. Окно конфигурирования потока

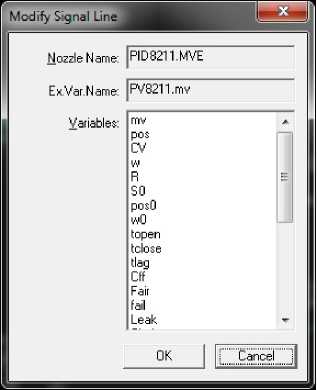
Рис. 4. Окно подключения датчиков

После того, как аппараты сконфигурированы, необходимо запустить модель на исполнение пунктом меню File, далее Execute. В режиме исполнения можно проверить получившуюся математическую модель и в случае необходимости внести в нее изменения.

Создание полной математической модели

Теперь, когда начальная модель отлажена, можно переходить к созданию полной математической модели, в которой будет учтено все технологическое оборудование. Также на данном этапе при необходимости простое оборудование заменяется более сложным, для расширения границ моделирования [ 4 ] .

После готовности модели для оптимизации времени можно создать несколько исходных состояний оборудования. Например: холодный, пуск, 50 % от стационарного состояния, установка, выведенная в стационар. Это позволит сократить время, необходимое для получения желаемого состояния процесса, с целью изучения его динамических характеристик.

Для расчета оптимальных настроек было выбрано 3 различных регулятора: уровня, давления и температуры.

При каскадном регулировании в качестве ведомого регулятора почти всегда используется регулятор расхода, а ведущим регулятором является регулятор температуры или уровня.

После того, как настроен ведомый регулятор, на принципах: максимальное быстродействие – минимальные колебания, он может рассматриваться как простой исполнительный механизм (клапан). После этого настройка верхнего контура каскадной АСР не будет отличаться от настройки одноконтурной АСР.

Получим переходную характеристику объекта до настройки регулятора со стандартными параметрами: интегральная составляющая – 10, пропорциональная составляющая – 100. Переходная характеристика приведена на рис. 5.

Так как роль исполнительного механизма в каскадном регулировании играет регулятор расхода, то кривую разгона получим путем изменения степени открытия клапана регулятора расхода потока питания.

Существует множество способов определения динамических параметров объекта из экспериментальных данных. В данном случае рассматривается наиболее простой, но эффективный способ, который заключается в том, что полученные данные аппроксимируются математической моделью, для которой заранее известны зависимости, определяющие оптимальные настройки регулятора. В качестве такой модели используются два динамических звена: апериодическое звено первого порядка и звено чистого запаздывания.

Задачей любого регулятора является приведение регулируемого параметра в соответствие заданному значению путем воздействия на соответствующий материальный или энергетический поток, т. е. действия любого регулятора направлены на устранение рассогласования между текущей и заданной величиной параметра [ 5 ] .

После получения оптимальных настроек регулятора получим апериодический переходной процесс с минимальным временем регулирования, поменяем уставку регулятора, для того чтобы получить переходный процесс для сравнения качества регулирования до и после настройки. Переходной процесс изображен на рис. 6.

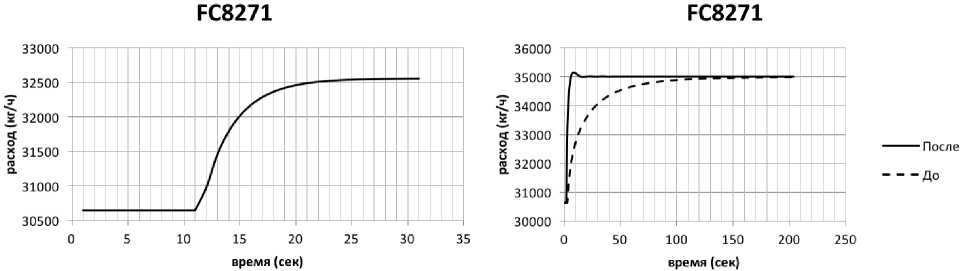
Рис. 5. Переходная характеристика                   Рис. 6. Переходная характеристика контура регулирования расхода                регулятора расхода до и после настройки

Описанным выше способом настроим остальные выбранные контуры. Переходные характеристики приведены на рис. 7–9.

LC8301

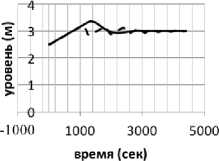
Рис. 7. Переходная характеристика контура регулирования уровня до и после настройки

РС8211

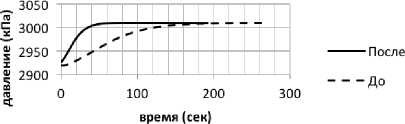
Рис. 8. Переходная характеристика контура регулирования давления до и после настройки

ТС8301

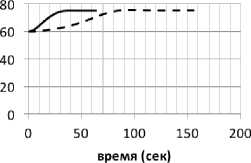
Рис. 9. Переходная характеристика контура регулирования температуры до и после настройки

Выводы

Компьютерное моделирование лежит в основе целенаправленной деятельности, смысл которой состоит в обеспечении возможности фактического эффективного выполнения на компьютере исследований работы сложных систем.

Программа Visual Modeler изначально содержит в себе большое количество математических моделей и возможность создания любой математической модели. В результате создания матема- тической модели в программе Visual Modeler для расчета оптимальных настроек регуляторов были получены переходные характеристики регуляторов, которые наглядно демонстрируют более качественный эффект настройки регуляторов.