Использование искусственной нейронной сети для криптоанализа шифра «Графические матрицы»

Постановка задачи

Основная идея шифра «Графические матрицы» (ГМ) состоит в том, что символы открытого текста представляют в виде матриц черных и белых точек (пикселей), которые описывают с помощью двоичной системы счисления. В процессе шифрования графические матрицы трансформируют по сложному закону, определяемому секретным ключом [1]. При шифровании исполь- зуют операции перестановок столбцов, строк, циклического сдвига, логического сложения с другой матрицей, сети Фейстеля и т.п.

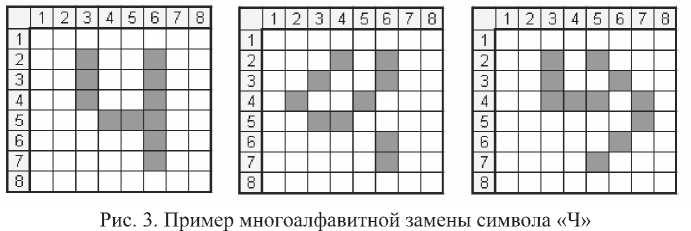
Простейший пример зашифрования символа показан на рис. 1. Матрица исходного символа «Ч» (рис. 1а) трансформирована путем циклического сдвига строк (рис. 1б) и циклического сдвига столбцов (рис. 1в). На рис. 2 показан пример зашифрования путем логического сложения по правилу Исключающее ИЛИ (шифр гаммиро-вания) исходной матрицы а) с матрицей б), в результате которого получена матрица в). Особенностью шифра ГМ является то, что вид символа открытого текста постоянно изменяется (даже в одном сеансе связи). Этот шифр можно отнести к шифрам многоалфавитной замены. Сказанное иллюстрирует рис. 3, на котором показан возможный вид одного и того же символа.

Рис. 1. Трансформация символа «Ч» с помощью операций циклического сдвига строк и столбцов

Рис. 2. Трансформация символа «Ч» с помощью логической операции «Исключающее ИЛИ»

Последовательность выполняемых при шифровании преобразований иллюстрирует рис. 4. Процесс шифрования состоит из двух этапов: предыскажения графической матрицы путем добавления аддитивного белого гауссовского шума и криптографического преобразования зашумленной матрицы:

M_i=f{T_i,K^ = T_i+N_i, (1) где М_; – предыскаженная матрица (результат первого шага шифрования); М^^к) – функция преобразования матрицы X на ключе К (первый шаг преобразований); Tj – i -ая матрица символа алфавита открытого текста; ^1 – «подключ» (далее без кавычек) – часть общего ключа К=№, используемый на первом шаге преобразования; N; – матрица шума.

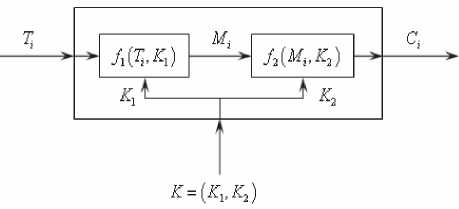
Рис. 4. Схема шифра «Графические матрицы»

Окончательное шифрование происходит в соответствии с выражением (2):

C=.UMi^ = MTANi^V   (2)

где c, – матрица шифртекста; M^x^ – функция преобразования второго шага матрицы X на ключе к (второй шаг преобразований); ^T – подключ общего ключа K = ^K_X,K.Y используемый на втором шаге преобразования.

Вносимая при кодировании с помощью графических матриц избыточность определяется по формуле (3).

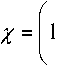
1M log₂^_v

•100%,

где h^o^ – энтропия источника открытого текста; N – объем алфавита шифртекста.

При энтропии источника открытого текста H^ = % бит (8-битные символы с равной вероятностью появления и объеме алфавита шифр-текста N = 2^M (для матриц 8×8), избыточность составляет х = ^,у/₀ .

При таком объеме вносимой избыточности представляет интерес исследование возможности использования искусственной нейрон- ной сети (ИНС) для криптоанализа указанного шифра.

Методика исследований

Были исследованы два метода шифрования ГМ: шифрование матриц методами гаммиро-вания и перестановок. Эти два метода шифрования ГМ являются аналогами классических методов замены и перестановок. Однако в классическом методе перестановок переставляются символы, а в шифре «Графические матрицы» переставляются пиксели матрицы. Это же можно сказать и о методе замены.

Методика оценки криптостойкости заключалась в следующем. Исследовалась способность нейронной сети правильно восстановить символы открытого текста, которые были искажены (трансформированы) в процессе шифрования и нанесения шума на матрицу. При этом восстановление символа в процессе распознавания нужно понимать, скорее, как предсказание наиболее вероятного вида символа. Окончательный выбор одного символа из нескольких символов с близкими вероятностями распознавания в процессе криптоанализа должен происходить с помощью цепей Маркова [2].

В процессе исследований предстояло ответить на вопрос о том, из какого состояния хаотического расположения пикселей еще возможно правильное распознавание символа. Для получения количественных оценок были использованы три варианта трансформации символа открытого текста: один заключался в том, что на исходную графическую матрицу наносился белый шум и исследовалась способность ИНС правильно распознать исходный символ. Заметим, что шум наносился в тех местах матрицы, где отсутствовало изображение самого символа.

Этот вариант можно считать особым случаем метода гаммирования, в котором единицы на матрицах гаммы и открытого текста не пересекаются. Второй вариант трансформации сводился к тому, что исходный графический символ демонтировался (пиксели отделялись от изображения символа и переносились в другие точки матрицы, не занятые самим символом). Таким образом имитировался метод перестановок. Третий вариант искажения символа использовался для исследования метода гаммирования (пиксели меняли цвет в зависимости от значения гаммы). Реализация ИНС была осуществлена с помощью матема-

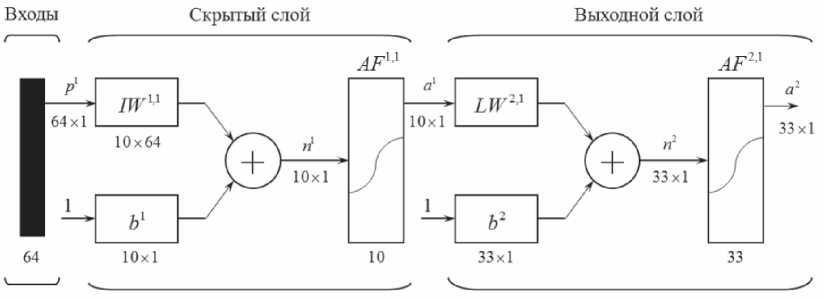
Рис. 5. Структура искусственной нейронной сети

тической системы MATLAB [3]. Для реализации распознавания символов использовалась ИНС со структурой двухслойного перцептрона [4].

Число входов совпадало с количеством элементов (пикселей) графической матрицы и для матрицы 8×8 пикселей составляло 64. Скрытый слой содержал 10 сигмоидальных нейронов. Количество нейронов в выходном слое совпадало с числом классов, то есть символов алфавита открытого текста, и равнялось 33. Функция активации нейронов выходного слоя – логистическая. Структура применявшейся ИНС показана на рис. 5.

В соответствии со структурой ИНС на вход первого слоя подавались 64-разрядные векторы-столбцы р . Каждый из входных векторов-столбцов умножался на вектор-строку входной матрицы весов IW^XA . Размерность последней зависел от числа нейронов в слое и размера входных векторов. В рассматриваемой сети размерность входной матрицы весов составляла 10×64. Взвешенные значения входов суммировались со скалярными значениями смещений первого слоя ь'. В результате формировались значения входов функции активации первого слоя и¹. Вычисленные значения активационных функций AF^X-X нейронов первого слоя формировали векторы выхода а . Выходной слой имел аналогичную структуру. Отличием являлось то, что выходной слой содержал 33 нейрона вместо 10 во входном слое, а также то, что размерность векторов входа совпадала с размерностью векторов выхода и составляла 10 элементов по числу нейронов первого слоя.

Для обучения на вход ИНС подавались не-зашумленные графические матрицы в виде символов русского алфавита. Обучающая функция реализована на основе метода градиентного спуска с моментами и с адаптивным обучением. Максимальное число циклов обучения было ограничено на уровне 5000. Для оценки функционирования сети была выбрана функция SSE (суммарная квадратичная ошибка), определяющая сумму квадратов ошибок обучения. Критерием окончания обучения была установлена величина отклонения от эталона равная 0,1.

Результаты исследований

При исследовании матриц, искаженных аддитивным белым гауссовским шумом, для каждого символа алфавита зашумление осуществлялось от 1 точки до полного заполнения матрицы с шагом в одну точку. При этом для каждого числа точек шума создавалось 10 различных вариантов матриц. Результаты распознавания матриц были усреднены по всем символам. Аппроксимированная зависимость процента успешных распознаваний от процента зашумления матрицы представлена на рис. 6.

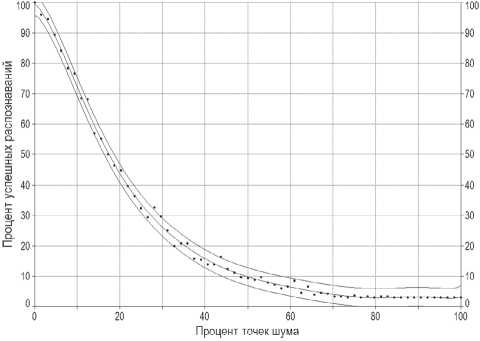
Рис. 6. Зависимость успешных распознаваний символов от степени зашумления

Из приведенного графика видно, что при наличии в матрице 18% пикселей шума вероятность правильного распознавания символа составит 0,5. При 60% шуме правильное распознавание становится практически невозможным. Вместе с тем при выполнении условий реализации шифра, когда в среднем четверть точек матрицы заполнена шумом, вероятность успешного распознавания матрицы составила 32,42%.

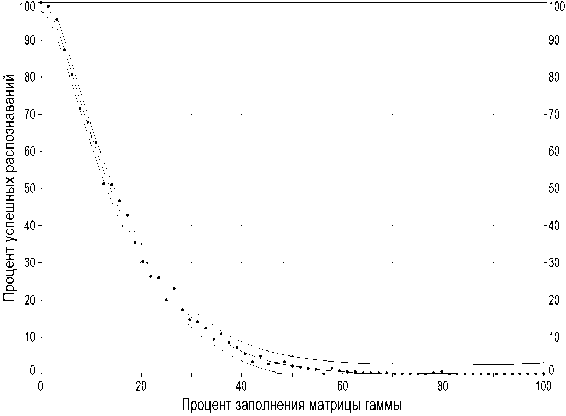
Рис. 7. Зависимость процента успешных распознаваний символов, искаженных операцией гаммирования, от степени заполнения матрицы гаммы

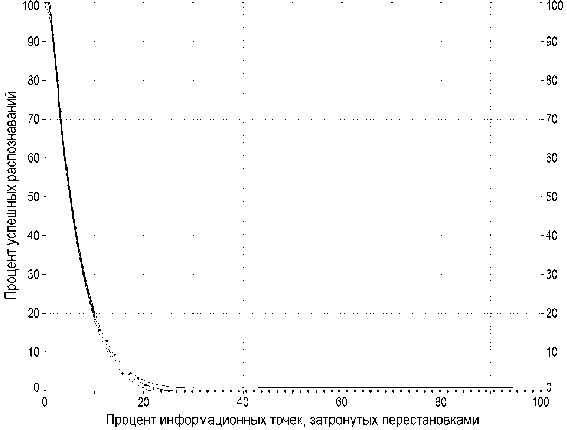
Рис. 8. Зависимость успешных распознаваний символов, искаженных перестановками, от процента черных точек матрицы, затронутых перестановками

При исследовании матриц, искаженных гаммированием, для каждого символа алфавита формировалась матрица гаммы, содержащая от 1 черной точки шума до полного заполнения с шагом в одну точку. Для каждого числа черных точек создавалось 10 различных вариантов матриц гаммы. Затем путем сложения чистых (неискаженных) матриц с матрицами гаммы по правилу «Исключающее ИЛИ» формировались наборы тестовых матриц. Результаты распознавания матриц были усреднены по всем символам. Аппроксимированная зависимость процента успешных распознаваний от процента заполнения матрицы гаммы черными точками представлена на рис. 7-8.

Графики рис. 7-8 говорят о том, что при типичной ситуации, когда в результате применения криптопреобразования в среднем половина точек меняет свое значение, ИНС не может правильно распознать матрицу.

Выводы

Искусственные нейронные сети могут быть успешно использованы для криптоанализа шифра «Графические матрицы» в тех случаях, когда анализируемая комбинация пикселей незначительно отличается от эталона (5…10%). Преобразование символов методом перестановок пикселей сложнее распознать, чем нанесение шума на матрицу – то есть метод перестановок более криптостоек по сравнению с методом гаммирования. Применение ИНС для атаки на метод перестановок не дает положительного эффекта (нет успешных распознаваний матриц). Сложнее распознать символ искаженный гаммированием, чем символ, искаженный белым шумом, когда шум не попадает на изображение символов.