Использование искусственных нейросетей для уточнения и анализа результатов атомно-силовой микроскопии дисперсно наполненных эластомеров (контактный и полуконтактный режимы)

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2025PNRPU MECHANICS BULLETIN

The paper proposes two new applications of artificial neural networks for decoding and analyzing results of the surface of elastomer nanocomposite scanning by means of atomic force microscopy (contact and semi-contact modes). The main advantage of this approach is that it enables studying local mechanical properties of the material not only on the sample surface but also in the near-surface layer.

In case of the contact operation mode of the atomic force microscope, the artificial neural network was created and "trained" using the database with the pressing models of the probe of the atomic force microscope into a nonlinear hyperelastic medium with rigid spherical inclusions ("contact neural network"). This database contained the results of calculations of indentation curves for various values of the filler particle sizes and their localization in the near-surface layer of the material (depth and horizontal distance from the tip of the probe). The use of such a neural network allows speeding up the construction of indentation curves by several orders of magnitude compared to conventional methods based on the numerical solution of the corresponding boundary value problems for each specific case. As a result, computing time is also significantly reduced, therefore, with an already constructed and "trained" neural network, powerful and high-speed computers are not needed.

In the semi-contact mode, the neural network was built using real scans of the relief and phase shift of the probe cantilever oscillations obtained on samples made of a dispersed filled elastomer ("semi-contact neural network"). It was shown that with its help it is possible to quite accurately predict what the results of the semi-contact scanning will look like with an increase in the maximum value of probe indentation (i.e. with a deeper study of the near-surface layer). Further, these modified scans are supposed to be used as a basis for analyzing near-surface layers using a contact neural network.

Развитие современных нанотехнологий в механике эластомерных композитов требует все более глубоких знаний о внутреннем строении материалов и их физических свойствах на микро- и наноуровне. Научившись эффективно управлять происходящими на этих масштабах процессами и явлениями, можно целенаправленно создавать наноструктурированные материалы с новыми потребительскими качествами, недостижимыми в рамках использования традиционных технологий. В настоящее время эта область материаловедения интенсивно развивается как в экспериментальном, так и теоретическом направлениях [1].

В экспериментальных исследованиях наиболее распространенными инструментами являются электронные [2–4] и атомно-силовые [2; 5; 6] микроскопы. С помощью электронной сканирующей и трансмиссионной микроскопии исследуются морфологические особенности структуры материала. Атомно-силовые микроскопы (АСМ) позволяют получать еще и дополнительную информацию о его «локальных» физико-механических свойствах на наноструктурном уровне (т.е. в масштабах, когда уже надо учитывать эффекты, связанные с особенностями молекулярного строения вещества, хотя сам материал еще можно считать сплошной средой). И эти «локальные» свойства могут существенно отличаться от макроскопических [7; 8].

Одновременно с экспериментами ведутся и теоретические исследования по структурному моделированию и описанию физико-механических свойств эластомерных композитов с учетом их внутреннего строения на микро-и наноуровне [9–12].

Фундаментальная задача данных исследований состояла в разработке новых методов расшифровки и анализа результатов атомно-силовой микроскопии, которые позволили ли бы значительно ускорить этот процесс, а также повысить его точность и надежность.

Как известно, в основе работы атомно-силового микроскопа лежит силовое взаимодействие между исследуемой поверхностью и зондом в виде консольной балки (кантилевера) с острым кремниевым щупом на свободном конце. В процессе эксперимента зонд АСМ сканирует выбранную поверхность образца. Получаемые при этом данные представляют собой зависимости между координатами точек сканирования, силой реакции, действующей на зонд, и глубиной проникновения вершины щупа в исследуемый материал. Эти результаты сами по себе (без дополнительных знаний о предмете исследований) малоинформативны, поэтому требуется их дальнейшая теоретическая расшифровка с привлечением различных физических и механических моделей [13–15]. Их разработка является важной и актуальной фундаментальной задачей.

В зависимости от характера действия силы между кантилевером и поверхностью образца выделяют три режима работы АСМ: бесконтактный, контактный и полу-контактный.

В бесконтактном режиме пьезовибратором возбуждаются колебания зонда на некоторой заданной частоте (чаще всего резонансной). Сила, действующая со стороны поверхности (взаимодействие Ван-дер-Ваальса), приводит к сдвигу амплитудно-частотной и фазово-частотной характеристик зонда. По этому сдвигу можно судить только о рельефе поверхности.

В контактном режиме (его еще называют наноинден-тацией) вершина зонда находится в непосредственном соприкосновении с поверхностью и монотонно вдавливается в образец в каждой точке сканирования. Это наиболее информативный (хотя и самый трудозатратный по времени) вариант.

В полуконтактном режиме также возбуждаются колебания кантилевера. В нижнем полупериоде колебаний кантилевер касается поверхности образца и вдавливается в нее (но не так сильно и не на такую глубину, как при наноиндентации).

Таким образом, контактный и полуконтактный режимы позволяют исследовать рельеф и локальные механические свойства не только на поверхности образца, но и приповерхностном слое. Толщина этого доступного для изучения слоя зависит от многих факторов: соотношения жесткостей кантилевера и сканируемого материала, прилагаемого к зонду усилия, адгезии на контакти-руемых поверхностях и т.д. Для определения его размеров и правильной расшифровки получаемой при наноиндентировании информации требуются соответствующие математические модели.

В данной работе рассматриваются только эластомерные нанокомпозиты, структура которых представляет собой комбинацию «мягкой» эластомерной матрицы и хаотично распределенных в ней «жестких» наночастиц наполнителя. Разрабатываемые для этого случая модели должны связывать механический отклик на внедрение зонда АСМ в структурно-неоднородный материал с формой и ориентацией дисперсных включений, а также их локализацией в приповерхностном слое (глубина внедрения и удаленность от точки индентирования). Наиболее очевидный способ их построения состоит в получении искомых зависимостей из решения соответствующих краевых задач механики деформируемого твердого тела. Оптимальным вариантом для этого случая представляется использование метода конечных элементов (МКЭ), так как он позволяет достаточно точно рассчитать локальные структурные напряжения и деформации в композите.

Но такой подход к созданию модели требует значительных вычислительных затрат так как приходится варьировать большое количество исходных параметров: физико-механические свойства эластомерной матрицы и частиц наполнителя; форма и размеры включений; глубина расположения в приповерхностном слое и удаленность от зонда АСМ и т.д. Кроме того, эти задачи должны решаться в трехмерной постановке, что также увеличивает трудоемкость расчетов. Но, даже получив на основе численных расчетов всю необходимую базу данных, построение надежной и эффективной итоговой модели (цифрового двойника [16; 17]), учитывающей совокупное влияние всех рассматриваемых параметров, является далеко не тривиальной задачей.

Главная проблема такого подхода в том, что если появляется необходимость ввести в модель какие-то дополнительные данные (результаты новых численных расчетов, увеличение количества исходных параметров), то ее каждый раз приходится полностью перестраивать заново (что весьма трудоемко и малоэффективно). Одним из возможных выходов из этой ситуации является использование искусственных нейронных сетей.

Искусственная нейросеть (ИНС) – это самообучающаяся математическая модель, построенная по принципу организации и функционирования биологических нейронных сетей. Нейросетевые программные комплексы способны не только выполнять однажды запрограммированную последовательность действий над заранее определенными данными, но и могут «самостоятельно» анализировать вновь поступающую информацию, находить в ней закономерности, производить прогнозирование и т.д.

В настоящее время искусственные нейросети считаются одним из самых передовых и перспективных направлений информатики. Они находят широкое применение в самых разных сферах человеческой деятельности: в медицине и биологии [18; 19]; криминалистике (распознавание людей и объектов на фото и видео) [20]; программах языкового перевода [21] и распознавания речи [22]; астродинамике [23; 24] и т.д.

В механике искусственные нейросети используются там, где требуется обработка результатов большого количества трудоемких и длительных вычислений: это предсказание механического поведения сложных конструкций при различных условиях нагружения [25] и их оптимизация [26]; определение эффективных механических свойств материалов на основе большого набора данных [27, 28]; прогнозирование механических свойств различных типов композитных материалов [29–31].

В данной работе представлены результаты применения искусственных нейросетей для уточненного анализа результатов контактного и полуконтактного АСМ-сканирования поверхности дисперсно наполненных эластомеров. Учитывая способность таких сетей к постоянному неограниченному развитию за счет поступления новых данных, с их помощью можно быстро и качественно проводить анализ физико-механических свойств композита, а также строить поля напряжений и деформаций на микро- и наноструктурном уровнях (аппроксимируя решения соответствующих краевых задач).

Авторы не ставили своей задачей детальную разработку правил и методических указаний, как наиболее эффективным образом создать искусственную нейросеть (ИНС), предназначенную для работы с результатами

АСМ сканирования. Их цель была скромнее – показать на частных примерах принципиальную возможность использования ИНС в атомно-силовой микроскопии.

Использование искусственной нейросети для расшифровки результатов работы АСМ в режиме наноиндентации («контактная нейросеть»)

Искусственную нейросеть для режима наноиндента-ции («контактная нейросеть») строили на основе набора решений контактных краевых задач о взаимодействии зонда атомно-силового микроскопа с поверхностью нелинейно-упругой конечно деформируемой среды, содержащей жесткое (недеформируемое) сферическое включение. Задачи решали численно в трехмерной постановке с использованием конечно-элементного пакета ANSYS (License No 1064623 ANSYS Academic Research Mechanical and CFD for IMSS Ural Branch of the Russian Academy of Sciences).

Расчетная схема представлена на рис. 1. Зонд АСМ (индентор) представляли в виде абсолютно жесткого параболоида вращения. Соответственно его профиль поверхности описывается как x =(2 Rz )^0.5 (где R – радиус кривизны в вершине зонда. Модельный образец имел форму прямоугольного параллелепипеда (эластомерная матрица), внутри которого размещалось жесткое сферическое включение радиусом R p . Оно располагалась на глубине z p от поверхности образца (расстояние от верхней точки сферы) и горизонтальном удалении x p от оси индентора (расстояние от центра сферы).

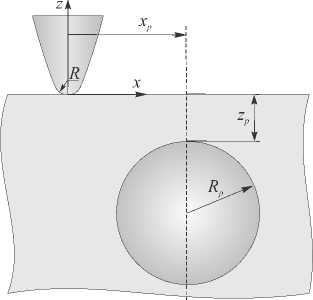
Рис. 1. Расчетная схема контактной краевой задачи об индентировании зонда АСМ в эластомерный композит

Fig. 1. Calculation scheme of the contact boundary value problem of indentation of an AFM probe into an elastomer composite

Размеры параллелепипеда образца составляли 1000 R по вертикали и 2000 R ×2000 R по горизонтали. Тем самым обеспечивалось условие отсутствия влияния удаленных границ на напряженно-деформированное состояние материала образца в зоне контакта. Эластомерная матрица считалась несжимаемой нелинейно-упругой средой, механические свойства которой описываются потенциалом нео-Гука (1)

W = ^ ( tr B - 3 ) , (1)

где w – плотность упругой энергии деформации эластомера, μ m – его модуль сдвига, tr B – след левого тензора Коши – Грина в полярном разложении деформационного градиента среды.

Нагружение системы производили за счет перпендикулярного вдавливания зонда АСМ в изначально плоскую поверхность образца. При этом на границе контакта выполнялось условие полного прилипания. Для удобства сравнения результатов глубина индентирования u изменялась от 0 (в момент касания зонда и поверхности) до одного и того же фиксированного значения u max .

Решение такой краевой задачи связано с серьезными вычислительными трудностями, обусловленными следующими обстоятельствами: 1) трехмерная геометрия задачи, что требует большой и сложной конечно-элементной сетки; 2) материал образца испытывает большие нелинейно упругие деформации; 3) наличие изменяемого в процессе нагружения контакта между зондом и образцом. В результате на каждый вариант численного решения (для конечно-элементной сетки, состоящей в среднем из 400 000 узлов и 550 000 элементов) требовалось порядка двух суток работы персонального компьютера класса Intel Core(TM) i5-6400. Традиционный путь, включающий перебор всех интересующих нас случаев взаимного расположения индентора и частицы наполнителя, требует огромного объема вычислений.

Однако если заранее создать базу данных, содержащую информацию о напряженно-деформированном состоянии в модельном образце, для некоторого ограниченного дискретного набора входных параметров, то на ее основе можно построить соответствующую искусственную нейросеть, которая связывала бы кривую ин-дентирования зонда АСМ с локализацией частиц наполнителя в приповерхностном слое относительно точки контакта.

Данный подход позволяет быстро и эффективно строить кривые индентации для непрерывного спектра значений входных параметров без решения соответствующих краевых задач. Кроме того, используя способность нейросетей к «самообучению» в модель можно без проблем вводить новые дополнительные данные из других решений краевых задач. Перестройка и усваивание этой информации «цифровым двойником» происходит автоматически. Таким образом, можно на несколько порядков ускорить алгоритм расшифровки результатов АСМ-сканирования и значительно повысить точность и надежность модели.

В нашем случае значения R p , x p , z p использовались в качестве независимых входных параметров модели. На выходе нейросеть давала индентационные кривые F ( u ), где F – сила упругой реакции зонда АСМ на вертикальное вдавливание в модельный образец; u – глубина вдавливания (индентация). Для примера, на рис. 2 показаны зависимости F ( u ) при наличии (1) и отсутствии (2)

жесткого сферического включения в эластомере, полученные из решения краевой задачи. Также было установлено, что при значениях x p порядка трех радиусов сферы и более включение практически не влияет на кривую ин-дентирования. Аналогичные расчеты при фиксированном x p =0 и варьируемом z p дали примерно те же предельные значения расстояния, на которых зонд АСМ еще «чувствует» включение (порядка двух радиусов сферы).

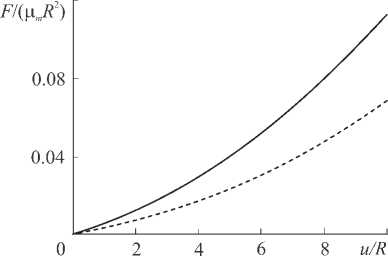
Рис. 2. Расчетные кривые индентирования зонда АСМ в модельный композитный образец. Сплошная линия – в образце имеется жесткое сферическое включение радиуса R p =5 R , расположенное в приповерхностном слое на глубине z p =5 R и горизонтальном удалении от оси зонда x p =5 R ; штриховая – включение отсутствует

Fig. 2. Calculated curves of AFM probe indentation into a model composite sample. Solid line – the sample contains a rigid spherical inclusion of radius R p =5 R , located in the near-surface layer at a depth of z p =5 R and a horizontal distance from the probe axis of x p =5 R ; dashed line – the inclusion is absent

Искусственная нейросеть, описывающая процесс ин-дентирования зонда АСМ в наполненный эластомер, была разработана и реализована в виде компьютерной программы на языке Python с использованием библиотек открытого доступа tensorflow.keras (конструирование нейросетей), numpy (работа с большими числовыми массивами) и matplotlib (представление полученных результатов в графическом виде). Библиотека tensorflow.keras содержит набор специальных базовых функций «примитивов», с помощью которых можно создавать нейросети с различной архитектурой, а также проводить их «обучение». Функции из библиотеки numpy применялись для преобразования получаемых из решения конечно-элементной краевой задачи данных в понятный для нейросети вид.

Сеть строилась в виде персептрона [32], состоящего из пяти последовательно расположенных слоев нейронов Sij (i – номер слоя, j – номер нейрона в слое). Каждый из них имеет прямую связь только с нейронами из соседних слоев (нейроны из одного слоя между собой не связаны). Архитектура персептрона схематически показана на рис. 3. С позиции математики каждый нейрон есть функция, зависящая от ni значений входных сигналов xk (k=1,…, ni), весов этих сигналов wk и активационной функции f, которая генерирует один выходной сигнал y = f (У n=1w wkxk I. Таким образом, каждый нейрон Sij передает одно и то же значение всем нейронам слоя S(i+1)j. В обратном направлении передача невозможна. В программе активационная функция имела следующий вид f =

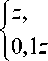
z >  0

z <  0,

Eni k=1 wkxk.

В первом (входном) слое было 4 нейрона (в него передаются значения входных параметров R p , z p , x p , u ), во втором – 32, в третьем – 64, в четвертом – 128. Пятый (выходной) слой состоял только из одного нейрона, содержащего итоговую информацию (сила упругой реакции на инденторе F ).

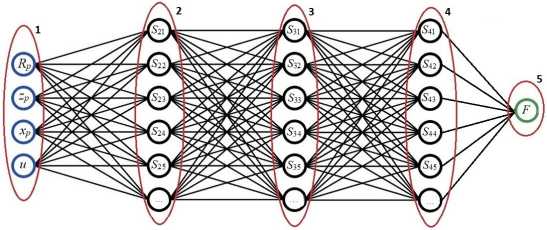
Рис. 3. Архитектура пятислойной искусственной нейронной сети

Fig. 3. Architecture of a five-layer artificial neural network

Алгоритм работы программы состоял из следующих этапов:

• •    на базе библиотеки tensorflow.keras строится исходная (необученная) искусственная нейросеть заданной конфигурации (но с еще неизвестными весовыми коэффициентами w i );

• •    для каждого набора геометрических параметров сети ( R p , x p , z p ) решалась соответствующая конечно-элементная контактная краевая задача (см. рис. 1). На основе этого решения рассчитывалась индентационная зависимость F ( u ), которая заносилась далее в базу данных в виде двумерного числового массива;

• •    для того чтобы использовать эти данные в качестве «обучающей выборки» их преобразовывали в требуемую для искусственной нейросети форму с помощью функций из библиотеки numpy;

• •    далее осуществлялся итерационный процесс подбора оптимальных значений весов для сетевых нейронов, то есть «обучение» нейросети. Итерации прекращались, когда среднеквадратичное отклонение распределения разностей между значениями F ( u ) «обучаемой» и «обучающей» (обучающая выборка) индентационных кривых становилось меньше заданной величины;

• •    обученная искусственная нейросеть сохранялась в отдельном файле (содержащем информацию о её конфигурации и всех полученных при обучении сети весах), готовом к дальнейшему использованию при расчете ин-дентационных зависимостей для произвольных значений параметров ( R p , x p , z p ), то есть для которых не было конечно-элементных расчетов.

Проведенные численные исследования показали, что в нашем случае для надежного «обучения» нейросети требовалось примерно от 1000 до 2000 итераций, что соответствует затратам компьютерного времени от 15 до 30 мин (для персонального компьютера типа Intel Core(TM) i5-6400), а построение собственно индента-ционной зависимости с помощью уже настроенной сети занимало доли секунды.

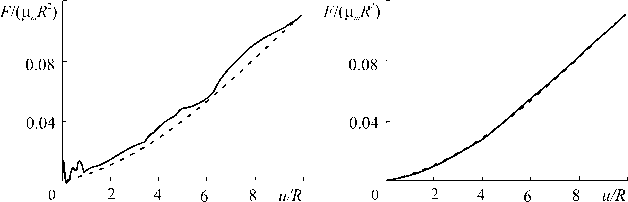
На рис. 4 представлен пример процесса обучения вышеописанной нейросети по мере увеличения количества итераций. В качестве тестовой выборки использовали конечно-элементное решение для случая R p =5 R , x p =5 R , z p =5 R . Кривые индентации F /(μ m R ²) – u / R , полученные непосредственно из решения краевой задачи, показаны штриховыми линиями, а аналогичные результаты, выданные нейросетью, – сплошными. На графиках видно, что на начальном этапе обучения (рис. 4, a ) нейросеть дает явно неудовлетворительную точность предсказания, особенно на начальном этапе индентации зонда АСМ – примерно до 1,5 R . На рис. 4, b, показаны результаты, полученные после 2000 итераций. Аппроксимирующая и тестовая кривые индентирования практически совпали, то есть процесс обучения можно считать законченным.

a                         b

Рис. 4 Кривые индентирования зонда АСМ после 500 ( a ) и 2000 ( b ) циклов обучения

Fig. 4 Curves of AFM probe indentation after 500 ( a ) and 2000 ( b ) training cycles

Для проверки работоспособности данного подхода были проведены расчеты по численному моделированию АСМ сканирования фрагмента поверхности эластомера (300 ×300 нм), содержащего жесткое включение в приграничном слое на глубине 50 нм по центру области. Эта поверхность разбивалась на прямоугольную сетку, и для каждого её узла строились силовые кривые индентиро-вания, для чего использовалась уже «обученная» нейросеть.

В реальных экспериментах на АСМ в качестве предельной фиксированной характеристики индентирова-ния чаще задается не глубина вдавливания зонда umax, а действующее на него максимальное усилие на конце зонда Fmax. Между этими параметрами имеется взаимно однозначное соответствие. Поэтому для большего удобства сравнения результатов моделирования с данными атомно-силовой микроскопии представленные ниже карты индентации строили для фиксированных значений Fmax =const.

При расчетах модуль сдвига эластомерного материала μ m считали равным 10 МПа, радиус скругления вершины зонда АСМ R= 10 нм, радиус включения R p =50 нм.

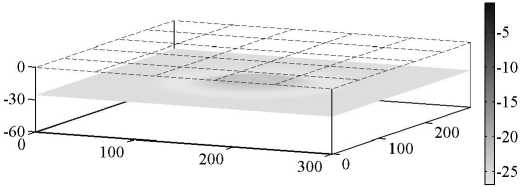
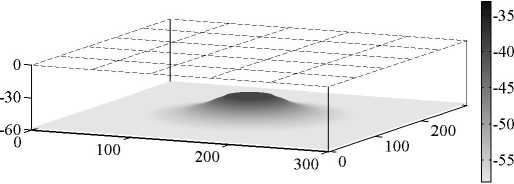
На рис. 5 показаны карты распределения глубины индентирования зонда АСМ. По вертикальной оси откладывалась рассчитанная с помощью нейросети инден-тация u (нм) . Нулевое значение соответствует поверхности образца (т.е. зонд в материал не вдавлен). Рисунок 5, а , соответствует F max =1,5^10^–4 нН, а 5б – F max =3,0^10^–4 нН. Анализ результатов расчетов показал, что нейросеть позволяет вполне отчетливо определить, где под поверхностью материала находится частица наполнителя, причем, чем больше максимальная сила вдавливания, приложенная к зонду, тем лучше это «видно». Данный подход вполне может быть использован при исследовании микроструктуры эластомерных нанокомпозитов с помощью атомно-силовой микроскопии.

а

b

Рис. 5. Карта индентации зонда АСМ в эластомерный материал, содержащий жесткое сферическое включение в центре области на глубине 50 нм от поверхности: а – F max =1,5^10^–4 нН; b – F max =3.0^10^–4 нН

• Fig. 5.    Map of AFM probe indentation into an elastomeric material containing a rigid spherical inclusion in the center of the region at a depth of 50 nm from the surface: a – F max =1,5^10^–4 nN;

b – F max =3,0^10^–4 nN

Использование искусственной нейросети для расшифровки результатов работы АСМ в полуконтактном режиме («полуконтактная нейросеть»)

К основным достоинствам полуконтактного метода по сравнению с контактным можно отнести то, что сканирование происходит намного быстрее, а зонд АСМ подвергается значительно меньшим механическим нагрузкам (и, соответственно, меньше изнашивается). Поэтому его широко используют при таких исследованиях, когда надо сканировать поверхности большой площади. Однако получаемые при этом режиме данные о структуре и механических свойствах приповерхностного слоя будут менее информативны, так как зонд вдавливается в поверхность образца существенно слабее, чем при наноиндентации. В данном разделе предлагается способ, позволяющий в определенной мере компенсировать этот недостаток за счет использования с помощью искусственной нейросети («полуконтактная нейросеть»).

Так как при полуконтактном режиме зонд АСМ находится в колебательном движении, то при описании его воздействия на образец используют не только глубину индентации (усилие на конце зонда), но еще и фазу сдвига колебаний, обусловленную взаимодействием со сканируемой поверхностью. Поэтому при создании и «обучении» ИНС применялся следующий алгоритм для определения исходной информации:

Сначала задавалась некоторая исходная глубина вдавливания зонда АСМ в поверхность u 0 . Она определяется амплитудой и частотой его колебаний, то есть ее можно устанавливать на нужную величину, варьируя настройки атомно-силового микроскопа. Значение u 1 выбирали так, чтобы обеспечить максимально возможный срок службы зонда (минимальный износ) и в то же время получить достаточный для дальнейшего анализа объем информации.

После этого производилось полуконтактное сканирование выбранного участка поверхности образца, на базе которого строились карты рельефа (высоты) и сдвига фазы колебаний зонда (механические свойства). Они сохранялись в виде соответствующих двумерных массивов: 1) матрица высот, 2) матрица сдвига фаз. На их основе строились две независимые нейронные сети (отдельно для высот и для фаз). Но при этом каждая ИНС в качестве входных данных использовала как матрицы высот, так и фаз.

Искусственная нейронная сеть для расшифровки результатов полуконтактного режима работы АСМ строилась на основе того же алгоритма, что и для контактного случая (см. предыдущий раздел). То есть снова использовались библиотеки открытого доступа tensorflow.keras, numpy и matplotlib. Компьютерная программа реализована на языке Python. Предварительные численные исследования показали, что в данном случае требуется значительно более сложная структура ИНС, что обусловлено намного большим объемом информации (на несколько порядков), которую должна «переработать» ИНС для выдачи результата. В итоге было установлено, что оптимальным вариантом будет использование не пяти (как это было ранее), а восьмислойного персептрона с увеличенным числом нейронов (с 229 до 2356), причем 1-й слой содержал 64 нейрона; 2-й – 128, 3-й – 128, 4-й – 256 нейронов, 5-й – слой 512 нейронов, 6-й – 512, 7-й – 256, а последний, 8-й слой (на выходе) – 500 нейронов.

В итоге сеть должна была обрабатывать экспериментальные данные АСМ-сканирования ограниченного участка поверхности наполненного эластомера в полу-контактном режиме с максимальной глубиной вдавливания зонда u = u 1 и делать прогноз об изменении этих результатов, если провести сканирование с другими значениями u = u 2 = k×u 1 , (где k варьировалось от 1,5 до 2,0).

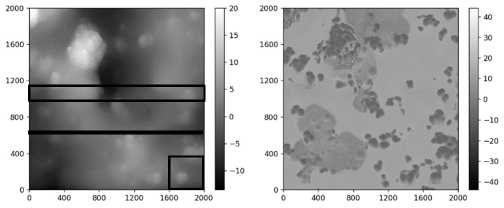
Для проверки работоспособности данного подхода использовались результаты полуконтактного АСМ-сканирования образцов из бутадиен-стирольного каучука марки СКМС-30АРКМ-15, содержащего частицы технического углерода (43 массовых частей) и детонационные наноалмазы (7 м.ч.). Жесткость частиц наполнителя на несколько порядков выше, чем у матрицы, то есть данный композит можно рассматривать как нелинейно упругую, конечно деформируемую среду, содержащую жесткие зернистые включения. При этом использовался зонд с радиусом вершины R =5 нм. Область сканирования имела размеры 2 × 2 микрон. Было проведено три независимых эксперимента на трех разных поверхностях. Результаты первых двух использовали для обучения нейросети, а на третьем проводилась проверка работоспособности предложенной методики. Экспериментальные сканы высот и сдвигов фаз оцифровывались в виде двух квадратных матриц H (рельеф) и ΔΦ (фазовые сдвиги) размером 500×500, которые и использовались в дальнейшем для построения соответствующих ИНС. Пример такой оцифровки представлен на рис. 6.

b

Рис. 6. Результаты полуконтактного сканирования образца из дисперсно наполненного эластомера: а – скан высот в нм; b – скан сдвигов фазы в градусах

• Fig. 6.    Results of semi-contact scanning of a sample made of dispersed filled elastomer: a – scan of heights in nm; b – scan of phase shifts in degrees

Для «обучения» нейронной сети матрицы H и ΔΦ должны быть преобразованы в так называемые обучающие выборки, понятные для используемых алгоритмов (далее для экономии места все выкладки приводятся только для матрицы H , так как в случае с ΔΦ всё было аналогично). В процессе исследований были опробованы три способа этих преобразований. Схематично они представлены на рис. 6, а (в виде квадрата, горизонтальной линии и узкой прямоугольной полосы).

Первый способ преобразования заключался в разбиении исходной матрицы H на (500/n)2 квадратных подматриц n×n. При расчетах значения n принимались равными 20, 25 и 50. Численные расчеты показали, что для нашего случая использование такой выборки для «обучения» ИНС не подходит – сеть так и «не смогла» выявить необходимые для прогноза закономерности.

Намного более эффективным оказался второй способ, когда матрица H разбивалась на 500 одномерных вектор-матриц размером 1×500 (то есть одна строка с длиной совпадающей числом столбцов в H ). В этом случае «обучение» было вполне успешным, и для получения приемлемой точности предсказаний (максимальное расхождение с экспериментом не более 5 %) требовалось порядка 8000 обучающих итераций (это примерно 5–6 ч для компьютера класса Intel Core^(TM) i5-6400).

Если же использовать для «обучения» не вектор-мат-рицы, а узкие прямоугольные подматрицы размером n ×500 (то есть опять на всю длину одной из сторон исходной области), то можно довольно существенно повысить точность предсказания за счет осреднения экспериментальных погрешностей. С ростом n время на каждую итерацию увеличивалось незначительно, а вот их количество возрастало в разы. Численные исследования показали, что оптимальным с точки зрения эффективности «обучения» оказался случай, когда n варьируется от 1 до 5.

Пример верификации ИНС для случая n =1 показан на рис. 7. Горизонтальной прямой линией показано расположение горизонтального сечения на матрице высот H (рис. 7, а ), для которого на рис. 7, b, представлено сравнение профилей рельефа: сплошная линия – эксперимент, штриховая – прогноз, полученный с помощью обученной ИНС (после 8000 итераций). Как видно из графика, совпадение результатов вполне удовлетворительное.

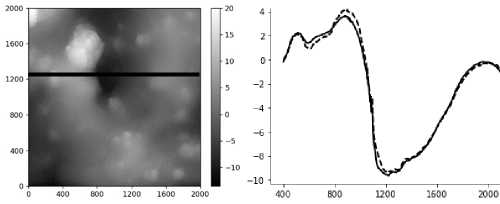
а

b

Рис. 7. Верификация результатов на примере матрицы высот: а – расположение горизонтального сечения (горизонтальная прямая линия); b – профили рельефа: сплошная линия – эксперимент, штриховая – искусственная нейросеть

• Fig. 7.    Verification of results using the height matrix as an example: а – location of the horizontal section (horizontal straight line); b – relief profiles: solid line – experiment, dashed line – artificial neural network

Ниже представлен пример, демонстрирующий использование «обученной» нейронной сети для предсказания результатов полуконтактного АСМ сканирования при разных максимальных глубинах вдавливания зонда u (то есть разных усилиях прижимания зонда к поверхности). На рис. 8, а, показаны результаты эксперимента при сканировании с u=10 нм, а на рис. 8, b – прогноз, полученный с помощью ИНС, обученной на экспериментах при глубине индентации u=7 нм (т.е. это попытка предсказать результаты сканирования, которые получились бы при увеличении прижимающего усилия на зонде). Как видно на графиках, результаты оказались вполне удовлетворительными.

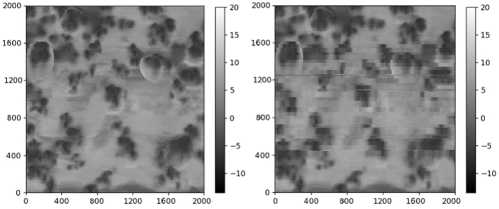
b

Рис. 8. Сравнение экспериментального АСМ скана высот (глубина вдавливания зонда 10 нм) ( a ) и аналогичного скана ( b ), построенного искусственной нейросетью на базе эксперимента с глубиной вдавливания 7 нм

• Fig. 8.    Comparison of the experimental AFM height scan (probe indentation depth 10 nm) ( a ) and a similar scan ( b ) constructed by an artificial neural network based on an experiment with an indentation depth of 7 nm

Наличие «горизонтальных полос» на рис. 8, b , связано с недостаточным количеством экспериментальных данных в обучающей выборке, которую использовали для иллюстрации работы метода. В нашем распоряжении было только три независимых экспериментальных скана: два из них использовались для «обучения» нейросети, а третий для моделирования с помощью ИНС новых цифровых сканов и их сравнения с исходными экспериментальными данными. Этого оказалось достаточно для подтверждения работоспособности предлагаемой методики, однако в случае ее практического применения объем «обучающей» экспериментальной информации должен быть увеличен. Причем одним из критериев ее достаточности как раз и можно использовать факт исчезновения этих полос.

Уточненные с помощью полуконтактной ИНС модельные сканы соответствуют большей глубине инден-тации зонда, и в принципе их вполне можно использовать как основу для более глубокого анализа приповерхностных слоев материала, но уже на основе контактной ИНС. Это позволило бы значительно сократить время работы АСМ, так как скорости сканирования в полукон-тактном и контактном режимах могут различаться в разы (в пользу полуконтактного варианта). Однако такой подход, несмотря на свою перспективность, требует серьезных дополнительных исследований, которые выходят за рамки данной статьи.

Заключение

Проведенные исследования показали перспективность использования искусственных нейросетей для расшифровки результатов атомно-силовой микроскопии при исследовании структуры и механических свойств приповерхностных слоев эластомерных композитов. Рассматривались два режима работы АСМ – контактный и полуконтактный. Для каждого из них предложен и реализован свой способ построения ИНС, учитывающий характерные особенности режима.

Контактная нейросеть позволяет быстро и наименьшими вычислительными затратами строить кривые ин-дентации, по которым можно оценить как локальные механические свойства материала, так и наличие частиц наполнителя в приповерхностном слое (глубину