Использование изменения системы отсчета для улучшения результатов анализа с помощью закона Бенфорда

Закон Бенфорда, также известный как закон первой цифры, представляет собой удивительное явление, наблюдаемое в различных наборах данных, где первая цифра чисел не распределена равномерно. Согласно этому закону, в естественных наборах чисел цифра 1 появляется значительно чаще, чем цифры 2, 3 и так далее, вплоть до 9.

Саймон Ньюкомб первым заметил, что «то, что десять цифр не встречаются с одинаковой частотой, должно быть очевидно любому, кто много пользуется логарифмическими таблицами и замечает, насколько быстрее изнашиваются первые страницы, чем последние».

После него уже Фрэнк Бенфорд обратил внимание на то, что «частота первых цифр близко следует логарифмическому соотношению F =log ( a + 1 ), где F - частота цифры a на первом месте используемых чисел».

Он повсеместно используется для обнаружения мошеннических схем в финансовой сфере, проверке выборов на фальсификацию и во многих других областях, где необходимо обнаруживать аномалии в больших объемах данных. Ведь различные манипуляции с данными меняют распределение первых цифр так, что они перестают подходить под закон Бенфорда.

В этой статье рассматривается возможность перевода значений в статистике в другую систему счисления для улучшения результатов анализа.

Распределение по закону Бенфорда в современном виде выглядит так:

1 P ( n ) =log b (1 + - ^)^

Где: n – первая цифра какого-либо значения в распределении; b -система счисления, в которой представлено распределение; P(n) – вероятность цифры n быть первой значащей.

То есть распределение меняется при переходе из одной системы счисления в другую, что и используется в этом методе.

Для исследования как набор анализируемых данных была выбрана площадь водосборного бассейна рек мира. Всего было использовано 171 значение. Анализ проводился в системах счисления: троичной, восьмеричной, десятичной, семнадцатеричной, шестидесятеричной и от тридцатидвоичной до тридцатидевятеричной.

На графике 2 обозначены:

• •    Черным – троичная система счисления.

• •    Красным – семеричная система счисления.

• •    Синим – десятеричная система счисления.

• •    Оранжевым – семнадцатеричная система счисления.

• •    Зеленым – тридцатишестеричная система счисления.

• •    Фиолетовым – шестидесятеричная система счисления.

Пунктиром обозначена функция закона Бенфорда, какой она должна быть в идеале, а сплошной линией – функция, получившаяся в результате анализа.

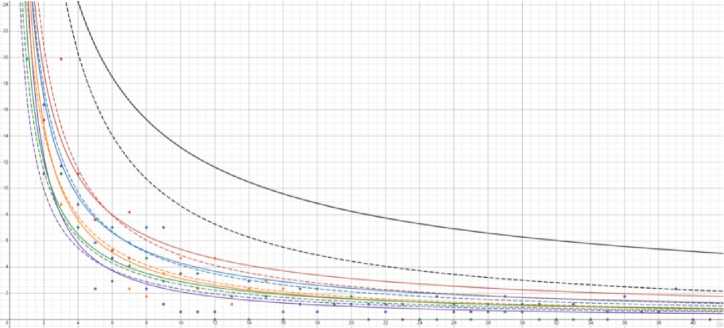
График 2. Результат вычислений.

При изучении получившейся функции можно понять, что качество анализа возрастает при увеличении системы счисления вплоть до тридцатишестеричной.

На наиболее маленьких системах счисления качество минимально, и аномалии в такой системе будут практически незаметны

Это объясняется тем, что увеличение системы счисления увеличивает количество возможных первых цифр, «размазывая» распределение, тем самым делая аномалии более заметными

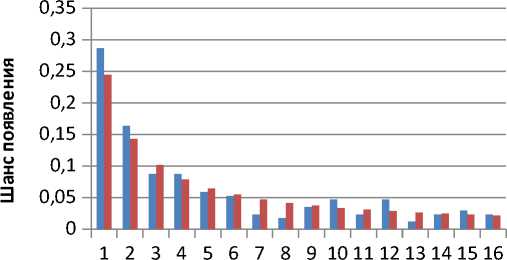
■ Измерение

■ Закон Бенфорда

Цифра

Таблица 1. Семнадцатеричная система счисления

Проблемы начинаются при значительном увеличении системы счисления, к примеру до шестидесятеричной (в тридцатишестиричной тоже иногда проглядывают искажения). При слишком большом увеличении функции становятся менее точными. Это можно объяснить тем, что основание системы счисления слишком приближается к количеству данных, хотя аномалии в такой системе все еще будут более заметными. Когда основание системы приближается к количеству анализируемых данных, количество анализируемых цифр увеличивается, и распределяемых на них значений не хватает, что делает такой анализ ненадежным. Вдобавок если приблизится к самим значениям, нарушится условие работы закона Бенфорда об охватывании нескольких порядков величин, и он может просто перестать работать.

Шестидесятеричная система счисления

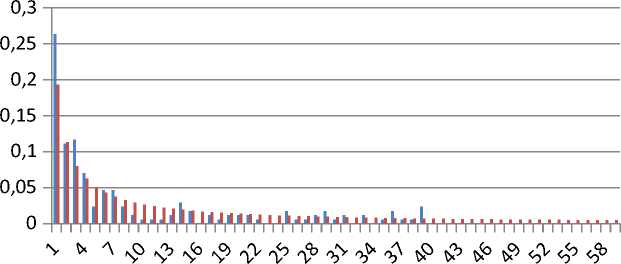
■ Измерения

■ Закон

Бенфорда

Таблица 2. Шестидесятеричная система счисления

В шестидесятеричной системе счисления точность становится очень маленькой (таблица 2), но зато аномалии появляются очень явно. Даже если взять большое количество данных, любое появление больших чисел означает аномалию, ведь шанс появления к примеру цифры 59 невероятно мал: 0,046%. И тем не менее точность анализа слишком низка

То есть для того, чтобы эффективно анализировать данные, основание системы счисления b в среднем должно быть минимум в 5 раз меньше количества анализируемых данных N

b

≤ ^N

Также можно уменьшить систему счисления, если в десятеричной системе нарушается условие охватывания нескольких порядков величин или имеется слишком мало данных.

Вывод: у этого способа присутствуют как и плюсы, так и минусы. При использовании этого метода необходимо подобрать оптимальную систему счисления, что может занять много времени, но тем не менее он значительно увеличивает обнаружимость аномалий.

Плюсы:

• •    Аномалии при увеличении системы счисления становятся гораздо заметнее, так как данные размазываются и шансы встречи больших первых цифр значительно уменьшается, что также помогает при анализе.

• •    При подборе подходящей системы счисления точность анализа может возрасти в отличие от десятеричной системы.

• •    Если факт присутствия аномалии был специально скрыт в десятеричной системе, аномалия может быть обнаружена в других системах счисления.

Минусы:

• •    Такой анализ может быть не всегда удобным, так как происходит не в привычной для нас десятичной системе счисления Может занять слишком много времени.

• •    Точность понижается при приближении к количеству данных или минимальным значениям анализируемой статистики, при слишком большом увеличении закон может вообще перестать работать.

Этот метод можно использовать либо в статистике с небольшим количеством данных для того, чтобы аномалии становились более заметными, либо в статистике с большим количеством данных для того, чтобы сделать анализ более точным. Точность анализа повышается не всегда, в некоторых случаях может уменьшаться. Тем не менее, основное преимущество этого метода заключается в том, что все аномалии в данных будут намного более заметными в больших системах счисления.

Желательно применять закон Бенфорда при анализе, совмещая разные методы. Например можно совместить метод увеличения системы отсчета вместе с методом анализа второй цифры, то есть анализировать и первую и вторую цифру в разных системах отсчета.