Использование эффектов взаимодействия акустической волны с заряженными атмосферными аэрозолями для оценки электрического состояния атмосферы

Электрическое состояние атмосферы оказывает значительное влияние на распространение радиоволн. Оно играет также важную роль в процессах образования локальных мезомасштаб-ных возмущений, генерации осадков, развитии и эволюции таких опасных явлений погоды, как град, гроза, смерч. Информация об электрическом состоянии атмосферы позволяет заблаговременно прогнозировать развитие чрезвычайных ситуаций, связанных с атмосферными явлениями. Наличие зарядов на гидрометеорах оказывает существенное влияние на обледенение и электризацию воздушных судов, работу их бортового радиоэлектронного оборудования. Кроме того, высокие значения напряженности электрического поля создают экологическую нагрузку на среду обитания и жизнедеятельность человека.

Отмеченный достаточно широкий, но далеко не полный спектр влияния электрического состояния атмосферы на возможность возникновения чрезвычайных ситуаций требует разработки методов, позволяющих проводить оценку электрических характеристик атмосферы и, соответственно, выявлять зоны с повышенной электрической активностью. Первопричиной возникновения вариаций электрического поля атмосферы выступает наличие в ней электрических зарядов Q, носителями которых служат аэрозоли – взвешенные в воздухе частицы различного происхождения.

В настоящее время данные о зарядах атмосферного аэрозоля получают контактными способами при использовании технических средств, устанавливаемых на борту воздушных судов, наземных ловушек, введением в исследуемую среду зондов с измерительными приборами [1–3].

Недостатком контактных способов является низкая пространственно-временная дискретность, невозможность получения информации в больших объемах пространства, искажение – 1154 – информации, обусловленное влиянием воздушных судов на характеристики электрического поля атмосферы, сложность получения информации о полях электрических характеристик и их изменениях в силу низкой пространственной дискретности контактных методов. Отмеченные недостатки не позволяют получать достоверную информацию об электрических параметрах атмосферы.

Таким образом, актуальность исследований, направленных на определение электрического состояния атмосферы неконтактными (дистанционными) методами, определяется не только их практической значимостью, но и нецелесообразностью использования существующих методов из-за присущих им недостатков.

Цель работы – повышение эффективности измерения параметров, характеризующих электрическое состояние атмосферы. Данная цель достигается путем разработки радиоакустического метода определения объемного заряда атмосферы, а вместе с тем и определения электрически активных зон.

Предлагаемый метод основан на зависимости интенсивности электромагнитного излучения аэрозольных частиц, частиц облаков и гидрометеоров (в дальнейшем просто заряженных частиц) от величины их заряда и ускорения движения. Известно [2–4], что при движении с ускорением электрических зарядов (заряженных частиц) они излучают электромагнитные волны. Если определенный объем атмосферы, содержащий заряженные частицы, подвергнуть воздействию акустических волн, то частицы будут вовлечены в движение атмосферного воздуха, вызванного акустическими волнами. Вследствие этого заряженные частицы, находящиеся в пределах данного объема, станут источниками излучения электромагнитных волн. Напряженность электрического поля электромагнитных волн, излучаемых совокупностью N частиц, находящихся в пределах объема, подвергшегося акустическому воздействию, является суперпозицией напряженностей Е i ( t ):

N q i a i ( t - ^{R i} )sin β

E(t) = ∑ c2 e-αRi , (1) i=1 4πε0c2Ri где qi – величина заряда частицы; ai(t) – ускорение движения частицы; ε0 – электрическая постоянная (диэлектрическая проницаемость воздуха), ε0 = 8,9·10-12 Ф/м; с – скорость распространения электромагнитной волны в вакууме; βi – угол между направлением движения частицы и направлением на точку, в которой наблюдается электромагнитная волна; δ – коэффициент ослабления напряженности электрического поля волны.

Поскольку движение аэрозольных частиц вызвано перемещением воздуха, созданного акустическим возмущением, то сила воздействия на частицу должна быть уравновешена силой, вызывающей ускорение движения частицы, и силой аэродинамического сопротивления со стороны воздуха. Такое равновесие сил определяется уравнением Даламбера:

d2x dx m + f = Fx(t) , (2) dt dt где m – масса частицы; f – динамическая вязкость воздуха; x – координата частицы вдоль направления действия силы Fx(t).

Обе силы, входящие в левую часть уравнения (2), при постоянных в течение действия силы Fx(t) плотности и форме частицы, будут зависеть от её размеров. Размеры частиц атмосферного аэрозоля, облаков, туманов, твердых и жидких осадков являются случайными величинами, имеющими плотность распределения f(r), где r – размер частиц. Кроме того, величина зарядов частиц также случайная величина, описываемая законом распределения f(q). Поэтому E(t) – случайный процесс. В силу этого оценка суммарного электрического заряда аэрозольных частиц, находящихся в объеме атмосферы, подвергнутому акустическому воздействию, может быть найдена с использованием характеристик случайного процесса E(t). Полное описание случайного процесса E(t) дается многомерными плотностями вероятности. Для оценки суммарного электрического заряда аэрозольных частиц объема атмосферы будем использовать математическое ожидание и корреляционную функцию E(t). Такой подход основывается на свойствах процесса E(t), зависящих от характеристик акустического воздействия. Зондирующие сигналы акустического локатора представляют собой последовательность импульсов, имеющих одинаковую длительность и период повторения. В каждом из импульсов мгновенные значения колебаний давления определяются соотношением p (t) = р. F (t) . sin(®t + ^0),                                                   (3)

где p(t) – мгновенное значение давления; P – амплитудное значение давления; А ( t ) – огибающая импульса

F ( t ) = Р при 0 "  t " ^т и ,                                                            (4)

[О при t > ти где τи – длительность импульса; ω=2πf – круговая частота изменения давления; f – частота; φ0 – начальная фаза, характеризующая давление в импульсе в момент времени t = 0.

Распространение зондирующего сигнала вызовет колебательное движение воздуха, имеющее мгновенную скорость

V ( t ) =         ,                                                                              (5)

зв где ρ – плотность воздуха; Сзв – скорость распространения акустической волны; ρСзв – удельное акустическое сопротивление воздуха.

В соответствии с выражениями (4) и (5)

P . _{F ( t})

V ⁽ t ) =         sin H + ^ 0) = V a F ⁽ t ^)sin( to t + ^ 0) ,                                ⁽⁶⁾

зв • ^p

P где Va =---- амплитуда скорости колебательного движения воздуха.

^P C зв

Амплитудное значение скорости колебательного движения частиц воздуха можно связать с акустической мощностью локатора W:

• - ^a R

• 1    Wе ²

V ( t ) = R ^ 2 ^^ ■ F ( t ) ■ sin( ® t ⁺ ^ o ) ,                                  (7)

v ^{p зв}

Характер и параметры этого движения могут быть найдены из решения уравнения (7), если переписать его таким образом, чтобы неизвестной функцией была скорость движения частицы.

m ( + fV ( t ) = F V ( t ) . dt

Если принять форму частиц сферической, а силу сопротивления – стоксовой, то уравнение (8) может быть приведено к виду

• 2    p- r ² dV_r ( t )

  -r + V r ( t ) = V ( t ) ,                                                         ⁽⁹⁾

• ^{9    n dt}

где V_r(t ) - мгновенная скорость колебательного движения частиц; V ( t ) - мгновенная скорость колебательного движения воздуха, определяемая формулой (7); ρ – плотность аэрозольных частиц; r - радиус частиц; п - динамический коэффициент вязкости воздуха.

Уравнение (9) является линейным дифференциальным уравнением с постоянными коэффициентами. Его решение будет простым в том случае, когда V(t) будет гармонической функцией, т.е. будет меняться по синусоидальному или косинусоидальному закону на бесконечном интервале времени. Вид функции V(t) определяется видом зондирующего сигнала p(t) (формулы 3–4). Реальные зондирующие сигналы акустических локаторов имеют конечную длительность и форму, отличающуюся от гармонического колебания, но они могут быть полностью представлены своими спектрами. Линейность уравнения (9) и возможность представления зондирующих акустических сигналов своими спектрами позволяют свести его решение к решению алгебраического уравнения. Применив прямое преобразование Фурье, получим

I 2 or2

9Пj” + 11 SV(”) = SV(^

^

где S V ( w ) и S i V ( w ) - комплексные спектры V_r(t) и V(t) соответственно.

Решив (10) относительно S_V ( w ) , после преобразования получим

^^Vr (Ю) = К (,);Sv (.),(11)

где                         12

K: (®) = ——,   y = - PL.

1+„.,„

Из соотношения (11) видно, что объем атмосферы, подвергнутый акустическому воздействию, можно представить в виде четырехполюсника, характеризуемого передаточной функцией (12). Используя обратное преобразование Фурье, найдем скорость колебательного движения частиц

∞∞

V r ( t ) = — f I C ( ® ) S V ( ® ) e^{3j A} d ® = — f ,          e "jarctg ^⁹ • S y ( ® ) e^Wd ® . (13)

'2n -»                    2n -« 1+ + p 2 ro2

Особенностью электромагнитных излучений частиц, находящихся в пределах импульсного объема, служит то, что они, имея импульсный характер, будут накладываться друг на друга, – 1157 – образуя случайный процесс. Случайный процесс E(t), определяемый выражением (1), выступает случайным процессом, представляющим собой наложение импульсов одинаковой формы:

a i ⁽ t ) =

dV_n( t ) dt

где V ri ( t ) - скорость колебательного движения частицы, определяемая выражением, например (14).

Импульсы имеют постоянную длительность, определяемую длительностью зондирующего сигнала. Амплитуда и фаза импульсов имеют случайные значения, так как коэффициент Y, определяющий амплитуду V r = v/ 71 + y 2 ® ² и фазу arctg Y® , зависит от размера частиц - г. Кроме того, значения зарядов частиц q_i , связанные с амплитудой E_i ( t ) прямой зависимостью, являются случайными величинами, имеющими плотность распределения f ( q ). Исследования, выполненные в [1], дают основание считать, что между величиной заряда q_i и размерами части нет устойчивой связи. Величина заряда в первую очередь определяется физическими особенностями его возникновения. Случайный процесс E ( t ) флуктуационный. Его реализации имеют вид непрерывных функций времени. Корреляционная функция и энергетический спектр процесса E ( t ) будут определяться видом функции a_i ( t ), описывающей ускорение движения частицы.

Определим a i ( t ) для типового акустического воздействия, создаваемого акустическим локатором (формула (3)), используя формулу (14). Значение V_r(t) найдем из выражения (13). Тогда, если i -я частица находится на удалении Ri , на основании формулы (7) имеем

R

V (t ) = VF (t — i-) _s ь _И + ^ 0 ) , ^Cзв

где V – амплитуда скорости колебательного движения воздуха, воздействующего на частицу.

Подставляя выражение (15) в (13) и интегрируя, получим ускорение, приобретаемое заряженными атмосферными частицами:

a to W    - TRi ai(t) = J e       F(t -

Ri ^{2np C}звCзв

t cos( tot + фо - arctg yto) + -sin( ^o - arctg yto)e '

Второе слагаемое в уравнении (16) характеризует переходной процесс. Учитывая его малый порядок, вторым слагаемым в уравнении (16) можно пренебречь. Для определения средней мощности излучаемого заряженными атмосферными частицами сигнала необходимо найти его автокорреляционную функцию. При этом a ( t ) удобно представить в комплексном виде:

ai ( t ) = A_t ( t ) e^J( ^ 0 - arctg ⁷® ) e^ ,

где

® i ( ) Ri

I

W  — Ri e2

2 np C зв

F ( t

^^^^^^e

^{R i} ) . C зв

Тогда автокорреляционная функция будет иметь вид

K изл

^(т )

I Z ) n                      .

---- E qia i ( t - 1 3 i ) Sin P i X

V 2 п у i=1

X

n

E q j = 1

*

a . ( t - t, .

j 3 j

+ т ) sin в

j

– постоянная величина.

где Z =       2

4п£ о c R

Таким образом, мощность излучения движущихся с ускорением заряженных атмосферных частиц будет определяться выражением

2 _n

Р изл ( т ) = К изл (0) = | Z | ^ q 2 A i ( t - t з _г ^т² Д ■ \ 2.K ) i =1

Величину суммарного заряда Q аэрозольных частиц можно получить по формуле

Q = 2 П        ^Ризл ^{( T} )

Z n

1 Z A2(t -13i)sin2 Pi i=1

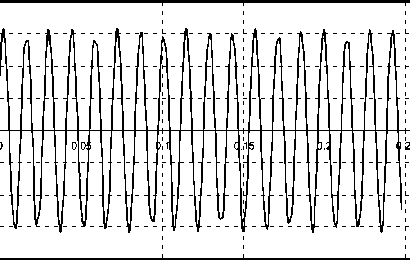
Практическая реализация предлагаемой методики была осуществлена по данным температурно-ветрового зондирования станции «Воронеж», характеризующим состояние атмосферы, и с учетом технических характеристик типового метеорологического акустического локатора: частоте акустической волны f = 2 кГц; длительности зондирующего импульса τ = 250 мс; акустической мощности излучателя W = 1000 Вт. Полученные результаты представлены на рис. 1.

Структура принимаемого электромагнитного сигнала, инициированного акустической волной, является реализацией случайного процесса, поэтому для его приема и последующей регистрации необходимо использовать энергетический приемник со средней частотой, равной частоте зондирующего акустического сигнала (ω). Вероятность обнаружения такого сигнала

0,00004

-0,00004

0,00002

0,00001

-0,00001

-0,00002

-0,00003

Еi, мкB/м   _0,00003

0,

,3

t, c

Рис. 1

энергетическим приемником равна Р_обн = 0,95 при вероятности ложной тревоги Р_л.т. = 10^–2 и отношении сигнал/помеха по мощности P c / P n = 25.

Для экспериментальной проверки предлагаемого метода был создан измерительный комплекс, состоящий из генератора акустических колебаний, динамика, источника заряженных аэрозольных частиц, приемника электромагнитного сигнала, аналогово-цифрового преобразователя, электронно-вычислительной станции с программным обеспечением и звуковым редактором Gold Wave 5.55 (рис. 2).

В процессе работы стенда излучался акустический сигнал с заданной частотой. При этом воздух ионизировался с использованием соответствующей установки. Выход антенного комплекса с согласованным усилителем был подключен на вход звуковой карты ЭВМ, где в дальнейшем проводилась его запись и анализ сигнала.

Задачей эксперимента явилось подтверждение возможности определения заряда атмосферы радиоакустическим способом. Исследования выполнялись при различных условиях с наличием акустического сигнала и без него с различной частотой акустического зондирования и мощностью излучаемого сигнала. В качестве примера на рис. 3 приведен результат экспери-

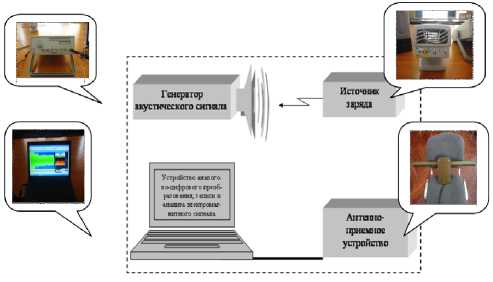
Рис. 2

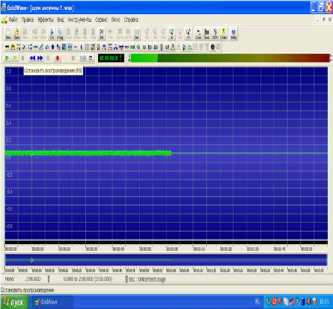
Рис. 3. Без акустического воздействия (а); при акустическом воздействии с частотой 6 кГц на заряженный объем атмосферы (б)

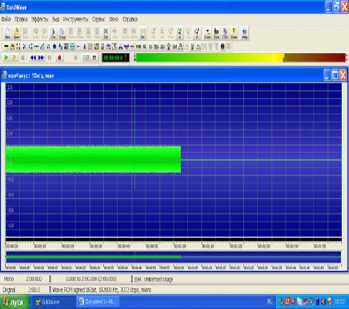
б

мента, проведенного при отсутствии акустического воздействия на заряженный аэрозоль и при включении акустического сигнала на частоте 6 кГц.

Таким образом, проведенные численный (с использованием осредненных данных многолетних наблюдений за метеорологическими и физическими параметрами атмосферы и данных о распределении физических характеристик по высоте) и натурный эксперименты показали работоспособность предлагаемого подхода к оценке электрического состояния атмосферы.