Использование кластерного подхода в повышении экономического потенциала нефтеперерабатывающего предприятия

Кластерный анализ - это динамично растущая дисциплина, которая является уникальным методом классификации объектов, связанных определенными характеристиками. Именно эта совокупность изучаемых объектов и является экономическим потенциалом.

Центральным понятием в кластерном подходе является понятие «кластер». «Кластер» обычно понимается как часть данных (зачастую это подмножество объектов или подмножество переменных, или подмножество объектов, характеризуемых подмножеством переменных), которые отличаются от остальных наличием определенного единообразия его элементов. Обычно речь идет о сходстве элементов кластера, в идеальном случае имеются совпадающие значения основных переменных или некоторый другой вид близости, выраженный геометрической близостью соответствующих объектов [1].

Основная задача кластерного анализа -разложить изучаемый набор объектов и его характерных признаков на однородные группы или кластеры в соответствующем смысле. Это указывает, что решается задача классификации исходных данных и определения соответствующей структуры. Методы кластерного анализа могут ис- пользоваться во многих случаях, даже если это простая группировка, в которой все сводится к группированию по количественному сходству.

Однородность или сходство означает близость объектов в многомерном пространстве атрибутов. Тогда задача сводится к размещению в этом пространстве естественных кластеров объектов, которые считаются однородными группами [1].

В общем случае понятие однородности объектов определяется введением «метрики» - правила расчета расстояний между парой объектов в данном наборе. Проблема расчета расстояний неизбежно возникает при любой интерпретации кластеров и различных методов классификации. В зависимости от метода, используемого для решения этой проблемы, методы кластерного анализа можно разделить на два типа: иерархический и неиерархический [2].

Евклидово расстояние является наиболее распространенным расстоянием и самой популярной метрикой в кластерном анализе. Это просто геометрическое расстояние в многомерном пространстве. Основным преимуществом этой метрики является то, что евклидово расстояние (и его квадрат) рассчитывается по исходным, а не по стандартизированным данным. Это обычный метод расчета, который имеет определенные преимущества. Например, расстояние между двумя объектами не изменяется, когда в анализ включается новый объект, который может оказаться выбросом (измерение, которое отличается от общей выборки и должно быть исключено). Рекомендуется использовать евклидово расстояние в тех случаях, когда знаки достаточно однородны по своему физическому значению, и было обнаружено, что все они одинаково важны с точки зрения решения проблемы отнесения объекта к тому или иному классу. Евклидово расстояние рассчитывается по следующей формуле:

Pe (X, xj )= JL (xi v i=1

^—

x j ^{) 2}

В зависимости от целей анализа, для придания большему весу объектов, которые находятся более далеко друг от друга, можно применять квадрат евклидова расстояния, для этого следует возвести в квадрат евклидово расстояние:

Pe (X, x ) L (xn- j i=1

Евклидова метрика, применяемая для вычисления расстояния между объектами, удовлетворяет всем аксиомам расстояния. Она не учитывает распределение точек в классе, а искажения евклидова расстояния не сильно влияют на результаты иерархических алгоритмов [2].

Было обнаружено, что на первом этапе при объединении объектов в отдельный кластер, расстояния между этими объектами определяются выбранной метрикой. Однако, кроме того, когда несколько кластеров соединены вместе, становится необходимым определить расстояние между кластерами. Другими словами, следует выбрать правило объединения для двух кластеров.

Имеются различные методы объединения кластеров, и метод кластерного анализа предлагает большой выбор этих мето- дов [3], в этом исследовании предлагается применять метод Варда, в некоторых источниках он называется методом Уорда.

Данный метод отличается от остальных тем, что применяет методы анализа отклонений для оценки расстояния между кластерами. Метод минимизирует сумму квадратов для любых двух (гипотетических) кластеров, которые могут быть созданы на любом этапе. На каждом шаге объединяются два кластера, что приводит к минимальному увеличению целевой функции, то есть внутригрупповой сумме квадратов. Таким образом, поля среднего значения будут находиться близко друг к другу и в структуре, поскольку они будут иметь большие значения пространственной корреляции. Метод Варда приводит к созданию кластеров примерно одинаковых размеров с минимальной внутриклассовой изменчивостью. В результате все объекты объединяются в один кластер [4].

Проанализировав различные методы кластерного анализа, каждый из которых дает несколько разные результаты, возникает вопрос о том, какой метод лучше всего применять на практике для оценки экономического потенциала нефтеперерабатывающего предприятия. По нашему мнению, в процессе создания классификаций существующих показателей субпотенциалов и определения степени их влияния на общий экономический потенциал должны применяться методы, учитывающие доступность имеющейся информации, имеющие практическую простоту расчета, позволяющие эффективно отслеживать изменения соотношения показателей в динамике и не вносить субъективности в расчеты.

Существует несколько рекомендаций практического плана выбора алгоритма кластеризации, полученных на основе экспериментального сравнения различных методов [5]. Изучив их и с учетом специфики нефтеперерабатывающей отрасли, на рисунке показан алгоритм оценки экономического потенциала нефтеперерабатывающего предприятия на основе кластерного подхода.

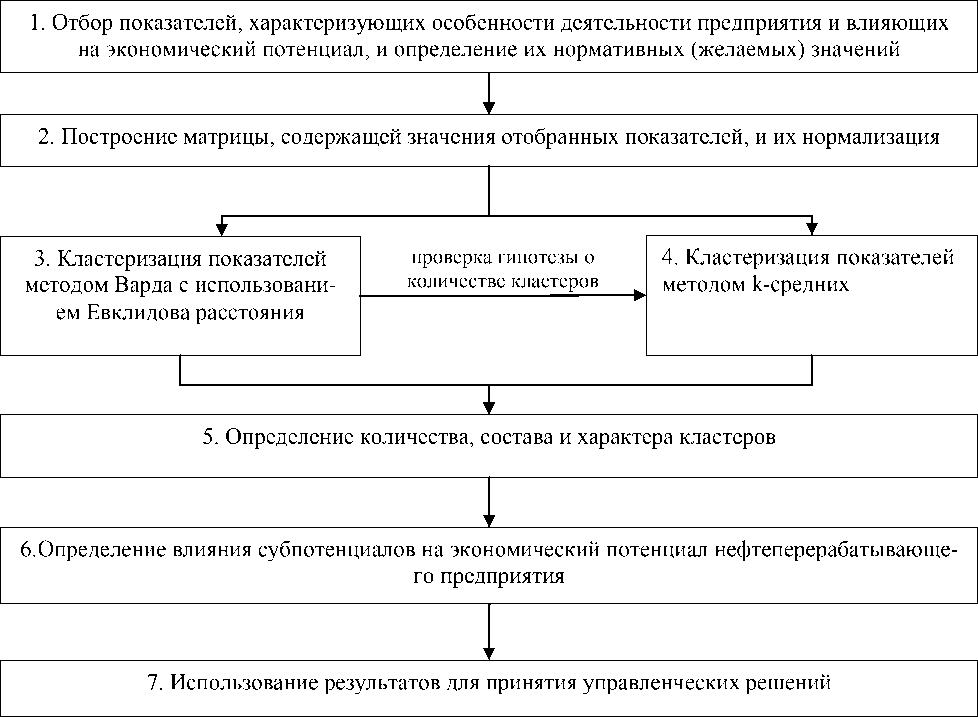
Рисунок. Алгоритм оценки величины экономического потенциала нефтеперерабатывающего предприятия на основе кластерного подхода

На первом этапе алгоритма проводится анализ и выбор показателей, влияющих на экономический потенциал нефтеперерабатывающего предприятия. На втором этапе строится матрица, которая содержит рассчитанные количественные значения показателей, выбранных на предыдущем этапе. Для достижения объективного анализа эти данные нормализуются, то есть приведены в одном измерении.

Третий этап - группировка нормализованных значений показателей, которые влияют на экономический потенциал нефтеперерабатывающего предприятия с применением метода Варда и евклидова расстояния. Использование этого метода кластеризации позволит нам проследить процесс выделения результирующих групп и проиллюстрировать подчиненность и содержание кластеров, которые будут состоять из наиболее похожих факторов.

Поэтому, чтобы проверить результат по количеству кластеров, на четвертой фазе алгоритма показатели группируются с использованием метода k-среднего. Этот метод позволит нам проверить гипотезы о количестве и составе кластеров. Если представление о количестве кластеров известно заранее, кластеризацию можно выполнить немедленно, используя метод k-среднего.

На пятом этапе для оценки каждого кластера рассчитывается ранее разработанный интегрированный показатель, который будет служить индикатором уровня экономического потенциала данного кластера.

Для проверки полученных результатов на шестом этапе определяется влияние на величину экономического потенциала каждого отдельного субпотенциала. Для этого сравниваются значения статистики F (уровня значимости), полученной путем расчета методом k-среднего для каждого показателя субпотенциалов экономического потенциала. Эти значения позволяют