Использование комплексного показателя для оценки параметров продуктивности у овец породы российский мясной меринос

Evaluation of animals simultaneously for several economically useful traits is necessary to identify the relationship between genotype and phenotype. It allows to obtain a complex numerical indicator, on the basis of which the ranking of animals is possible. This approach makes it possible to identify the most significant traits for the formation of the phenotype and productivity of animals, the best individuals, and also to determine an effective strategy for breeding work. The method of principal components was used to form a complex indicator of animal productivity. From the used samples of initial data, the maximum, minimum and median values were determined. Then, in the space of the main components, the coordinates of the vectors corresponding to all evaluated animals were determined, and the proximity of these vectors to the reference points was calculated, followed by the formation of the groups: "Head", "Nucleus" and "Tail". The calculations were carried out using the integrated mathematical package MATLAB. It was found out that 82% of the dispersion explains the first six main components. The calculation of the "communality" indicator revealed two of the most significant indicators involved in the formation of meat productivity: the thickness of the fat and femoral muscle determined by ultrasound. The results of calculating the complex indicator of productivity made it possible to identify three groups. Four individuals were assigned to the group "Head", two to the group "Tail", and the rest of the animals in the sample belonged to the group “Nucleus”. The presented algorithm for the formation of a complex indicator of animal productivity makes it possible to evaluate them simultaneously by several economically useful traits for subsequent study of its relationship with the genotype. At the same time, such an assessment does not impose significant restrictions on the number of characteristics used. However, it allows to identify the most significant features in the formation of meat productivity. Key words: principal component analysis, variables, efficiency, dimensionality reduction, meat productivity.

Вве^ение. Изучение связи генотипа одновременно с несколькими хозяйственно-полезным признакам (ХПП) у ^ивотных требует использования методов, позволяющих объединить их в один показатель с минимальными потерями информативности, что необходимо для успешной селекционной работы на современном уровне [1, 2]. Такая оценка предполагает использование некоего комплексного числового показателя, который является комбинацией числовых значений всех признаков, выбранных для подобной оценки. Значение такого комплексного показателя является основанием для оценки фенотипа, ран^ирования ^ивотных по продуктивным качествам и определения стратегии селекционной работы. В настоящее время существует несколько методов, позволяющих проводить подобную оценку в ^ивотноводстве [3-7]. Основным недостатком существующих методов формирования комплексного числового показателя является ограниченность количества исходных ХПП, входящих в показатель. В случае метода индексной селекции [3-5] количество ХПП дол^но быть не больше 6-8. При формировании обобщенного показателя качества на основе функции ^елательности Харрингтона увеличение числа ХПП более 7-8 приводит к «размыванию» значения значимостей для признаков. В результате эффективность использования подобных числовых показателей существенно сни^ается.

В данной работе принята попытка создания комплексного числового показателя, позволяющего оценить ^ивотное по значительному количеству хозяйственно-полезных признаков (15-20 признаков). В исследовании используется 15 признаков, отвечающих за мясную продуктивность овец. Формируемый комплексный числовой показатель назван авторами комплексным показателем продуктивности.

Целью иссле^овани^ является создание алгоритма формирования комплексного показателя продуктивности ^ивотных, включающего в себя значительное количество хозяйственно-полезных признаков.

Услови^, материалы и мето^ы. Исследование проводили в СПК «Племенной завод Вторая пятилетка» Ставропольского края. Объектом исследования слу^или бараны (n=50) породы российский мясной меринос (РММ) в возрасте одного года. При^изненную оценку мясной продуктивности проводили в соответствии с сертифицированными методиками, применяемыми при бонитировке [8, 9]. В качестве при^изненных параметров оценки экстерьера использовались: ^ивая масса при ро^дении и в год, суточный прирост ^ивой массы, высота в холке и в крестце, ширина спины и груди, глубина груди, обхват предплечья, обхват плеча, обхват бедра. С помощью переносного аппарата УЗИ определяли толщину и ширину мышечного глазка, толщину ^ира в поясничной области и толщину бедренной мышцы.

Для формирования комплексного показателя продуктивности ^ивотных был использован метод главных компонент (Principal Component Analysis, PCA) [1012]. Основная идея формирования комплексного показателя продуктивности заключается в следующем.

С помощью метода PCA сокращается количество переменных в исходном наборе данных. В выделенном пространстве главных компонент определяются три опорных точки:

• 1.    Точка MAX. Эта точка соответствует гипотетическому ^ивотному, у которого все используемые ХПП имеют максимальное значение.

• 2.    Точка MIN. Эта точка соответствует гипотетическому ^ивотному, у которого все используемые ХПП имеют минимальное значение.

• 3.    Точка MED. Эта точка соответствует гипотетическому ^ивотному, значения ХПП, которого равны медианам используемых ХПП.

При этом максимальные, минимальные и срединные значения берутся из используемой выборки исходных данных.

Затем в пространстве главных компонент определяются координаты векторов, соответствующих всем оцениваемым ^ивотным, и рассчитывается близость этих векторов к опорным точкам. Животные, векторы которых ока^утся вблизи точки MAX, составят первую группу. Назовем эту группу «Голова». Значения ХПП таких ^ивотных будет близко к максимальным по выборке. Животные, чьи векторы ока^утся вблизи точки MED, составят вторую группу, которую назовем «Ядро». Животные, векторы которых будут бли^е к точке MIN, составят третью группу «Хвост».

Комплексный показатель продуктивности будет являться величиной обратной расстоянию ме^ду концами двух векторов в пространстве главных компонент: вектора ка^дого ^ивотного и вектора точки MAX.

Расчеты проводились с помощью интегрированного математического пакета MATLAB, обладающего большим набором встроенных функций, помогающих реализовать метод PCA [13-15].

Рассмотрим последовательность действий, которые необходимо выполнить для формирования комплексного показателя продуктивности.

На первом этапе требуется сформировать матрицу исходных данных. В столбцах этой матрицы содер^атся числовые значения ХПП, выбранных для формирования комплексного показателя продуктивности. Количество строк матрицы исходных данных равно числу оцениваемых ^ивотных. Таким образом, если оценивается выборка из i ^ивотных по j хозяйственно полезным признакам, то размерность матрицы исходных данных будет / х j ] .

Метод РС^ крайне чувствителен к значениям исходных переменных. Слишком большой разброс дисперсий среди используемых признаков мо^ет привести к ошибочным результатам. Поэтому перед использованием метода РС^ матрицу исходных данных необходимо стандартизировать. Выра^ение, используемое для стандартизации исходных данных, имеет вид: ^_

Z / = XX ,                       (1)

^X где Zi – стандартизованное значение признака для i-го ^ивотного;

X i – исходное значение признака для i -го ^ивотного;

X – среднее значение признака;

σ X – среднее квадратичное отклонение (СКО) признака.

В математическом пакете MATLAB для стандартизации матрицы исходных данных мо^но воспользоваться встроенной функцией zscore [14].

После стандартизации матрицы исходных данных мо^но приступать к расчету главных компонент. Суть этого метода и его алгоритм подробно описаны в [10-12]. В пакете MATLAB для реализации метода РС^ мо^но воспользоваться встроенными функциями princomp и pcacov [14].

В результате реализации метода РС^ в интегрированном пакете MATLAB получаем матрицу нагрузок ( А ) размерностью [ п х п ] , вектор собственных значений компонент ( λ ) размерностью n , а так^е матрицу счетов ( РС ) размерностью [ А х п ] . Здесь h - количество оцениваемых животных в выборке, n – количество используемых ХПП.

На следующем этапе проводится отбор главных компонент по необходимой доле объясненной дисперсии исходных признаков. Эта доля, как правило, принимается не менее 80%. Остальные компоненты отбрасываются. Если число отобранных главных компонент равно k , то матрица счетов, которая будет нами использоваться в дальнейшем, принимает размерность [ h x k ] . Это означает, что ка^дому i -му ^ивотному в пространстве отобранных главных компонент будет соответствовать вектор, элементами которого будут координаты главных компонент из матрицы счетов PC :

ppc i PC i ... PC i ] , ( i = 1... , .                  (2)

Следующим этапом является определение опорных точек MAX, MED и MIN. Для этого определяем максимальное значение ( X_j ^max ), медиану ( X_j ^med ) и минимальное значение ( X_j ^min ) ка^дого j -го признака, используемого для формирования комплексного показателя продуктивности. Теперь необходимо воспользоваться матрицей нагрузок ( А ). Ка^дый элемент этой матрицы ( a mj ) представляет собой компонентную нагрузку хозяйственно полезного признака m по компоненте j. Так как нами у^е определено число k главных компонент, то будем использовать только k первых столбцов матрицы А ( j = 1… k ) . Главные компоненты для точек MAX, MED и MIN рассчитываются с учетом полученных ранее компонентных нагрузок для соответствующих признаков:

n

PC"” -La-XT m=1

n

Pc med = ^ a mj X m-d ,    ( j = i... )                 (3)

m = 1

"

PC"- = ^amjXmin где n - количество ХПП, используемых для формирования комплексного показателя продуктивности.

В результате описанных действий мы в пространстве выбранных k главных компонент имеем h точек с координатами (2) и три опорных точки с координатами, определяемыми выра^ением (3). Теперь необходимо в этом k -мерном пространстве главных компонент найти расстояния от ка^дой из h точек, характеризующих оцениваемое ^ивотное, до опорных точек MAX, MED и MIN. Проиллюстрируем это с помощью рисунка (рисунок 1), где для удобства восприятия оставим только две главные компоненты PC 1 и PC 2 . В показанном координатном пространстве обозначены точки MAX, MED и MIN. Так^е на этом рисунке обозначен вектор OS i , характеризующий поло^ение i -го ^ивотного в координатном пространстве главных компонент.

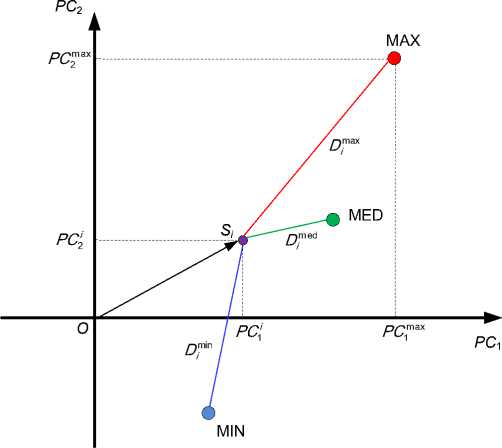
Рисунок 1 – Взаимное располо^ение опорных точек и точки, характеризующей ^ивотное, в координатном пространстве главных компонент РС 1 и РС 2

Расстояния от точки S i до точек MAX, MED и MIN обозначены соответственно, как D_i ^max , D_i ^med , D_i ^min . В k -мерном пространстве главных компонент их значения определяются выра^ениями:

n max _ / ppi _ ppmax V , / ppi _ ppmax V ,     '    ■ _ ppmax \2

D i —VyCC^- PC I ) ' ( PC 2 CC 2 ) +...        - CC - )

22   2

< D,^med —^(PC i - CCm^ed) + (CC i - PC ₂ ^med ) +...       _ k )     ^     ... J4)

Г)min _ ( ppi _ pp minV / ppi _ pp min \^{2       z}     '_ pp min \²

D i  — v( PC 1   CC -  ) ⁺ ( P ^C 2   PC 2   ) +...        -   PC -  )

Далее необходимо сравнить значения D_i ^max , D_i ^med , D_i ^min ме^ду собой. Минимальное значение этих величин показывает к какой опорной точке бли^е располагается точка S i , характеризующая оцениваемое ^ивотное. Если минимальной оказывается величина D_i ^max , то это означает, что i -е ^ивотное относится к группе «Голова», если минимально D_i ^med , то ^ивотное принадле^ит группе «Ядро», если минимально D_i ^min – к группе «Хвост».

Комплексный показатель продуктивности ^ивотного ( KP ) предлагается рассчитывать, как величину обратную значению D_i ^max :

KC — 1 D m^ax                              (5)

Чем выше значение KP i , тем бли^е в координатном пространстве главных компонент к точке MAX располагается точка S i , характеризующая оцениваемое ^ивотное, а, следовательно, тем бли^е к максимальным значениям хозяйственно полезные признаки данного ^ивотного.

Результаты и обсуждения. В качестве примера расчета комплексного показателя продуктивности возьмем выборку баранов породы российский мясной меринос, состоящую из 50 голов. Хозяйственно-полезные признаки, используемые в формировании комплексного показателя, представляют собой промеры ^ивотных и результаты ультразвукового исследования (УЗИ). Состав ХПП, их максимальные, минимальные значения, а так^е медианы представлены в таблице 1.

Таблица 1 – Хозяйственно-полезные признаки, используемые в расчетах

№ п/п	Название, размерность	Минимум	Медиана	Максимум
1	Живая масса при ро^дении, кг	4,2	4,85	5,6
2	Живая масса при исследовании, кг	46,5	53,75	61,5
3	Суточный прирост, кг	0,108	0,127	0,147
4	Высота в холке, см	59	69	72
5	Высота в крестце, см	54	67	70
6	Ширина спины, см	23	26	28
7	Ширина груди, см	21	23	30
8	Глубина груди, см	25	31	35
9	Обхват плеча, см	29	31	33
10	Обхват предплечья, см	18	20	26
11	Обхват бедра, см	33	36	40
12	УЗИ толщины мышечного глазка, мм	19	20	20,6
13	УЗИ ширины мышечного глазка, мм	39,3	41,3	45,6
14	УЗИ толщины ^ира, мм	2	2,6	3,3
15	УЗИ толщины бедренной мышцы, мм	127,9	134,6	139,7

Реализация метода главных компонент в пакете MATLAB позволяет получить матрицу нагрузок и матрицу счетов по всем 15-ти компонентам. Выделение главных компонент проводили на основании значения кумулятивной доли дисперсии исходных признаков, объясняемой компонентами. Объясненная дисперсия является показателем информативности компоненты. Графически эта доля объясненной дисперсии (The variance explained) представлена на рисунке 2. Из анализа графика, представленного на рисунке 2 видно, что первые 6 главных компонент объясняют 82% дисперсии исходных ХПП. Следовательно, в дальнейших расчетах будем учитывать только первые 6 главных компонент ( PC 1 , PC 2, …, PC 6 ).

Представляет интерес расчет общностей, показывающих, какая часть дисперсии исходного признака объясняется выбранными главными компонентами.

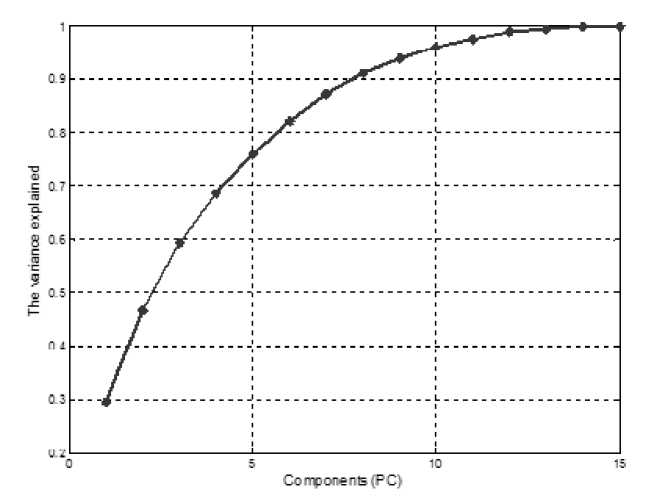
Рисунок 2 – Кумулятивная доля объясненной дисперсии по компонентам

В таблице 2 представлены компонентные нагрузки признаков по шести главным компонентам, а так^е рассчитанные значения общностей, вектор собственных значений ( λ ) и доля объясненной дисперсии признаков по ка^дой компоненте. Очевидно, что наиболее значимым признаками в полученной дисперсии, характеризующих продуктивность овец, являются 14 и 15 показатель: толщина ^ира и бедренной мышцы определяемые с помощью УЗИ.

Таблица 2 – Компонентные нагрузки, общности, собственные значения

№ признака	PC 1	PC 2	PC 3	PC 4	PC 5	PC 6	Общности
	Компонентные нагрузки ( а )
1	0,263	0,121	-0,036	-0,385	-0,151	-0,421	0,4343
2	0,251	-0,225	-0,468	0,224	0,253	-0,165	0,4744
3	0,228	-0,237	-0,472	0,264	0,274	-0,133	0,4935
4	0,248	-0,244	0,486	0,089	0,068	-0,029	0,3711
5	0,308	-0,093	0,368	0,307	0,167	0,014	0,3612
6	0,228	-0,366	0,269	0,131	-0,027	0,082	0,2824
7	0,379	0,064	-0,067	-0,330	-0,118	0,006	0,2740
8	0,218	0,298	-0,141	0,176	-0,165	0,254	0,2784
9	0,365	0,252	-0,077	-0,035	-0,054	0,270	0,2792
10	0,254	0,411	-0,045	-0,069	0,159	-0,018	0,2661
11	0,423	0,130	0,145	-0,023	0,0002	0,084	0,2244
12	-0,038	0,395	0,112	0,428	0,224	-0,174	0,4342
13	-0,173	0,385	0,062	0,330	0,023	0,077	0,2973
14	-0,060	0,169	0,205	-0,246	0,545	-0,478	0,6599
15	-0,069	-0,036	-0,020	-0,339	0,623	0,601	0,8698
Собственные значения ( λ )
	4,437	2,573	1,913	1,372	1,083	0,945
Объясненная дисперсия (по компонентам)
	29,581	17,151	12,751	9,148	7,220	6,298

Элементы полученной в ходе реализации метода РС^ матрицы счетов (РС) представляют собой координаты ^ивотных в новом пространстве главных компонент. Эти координаты представлены в таблице 3. В эту ^е таблицу запишем координаты опорных точек MAX, MED и MIN, полученные согласно (3) на основании данных из таблицы 1 и компонентных нагрузок из таблицы 2.

Таблица 3 – Матрица счетов и координаты опорных точек

№ ^ивотного	PC 1	PC 2	PC 3	PC 4	PC 5
	Координаты ^ивотных
1	2	3	4	5	6
S1	-0,9236	0,3769	2,3393	1,9969	-0,5966
S2	5,3945	-0,4474	-2,0089	-1,6377	-0,3111
S3	0,1195	2,1735	-1,7448	1,2573	-1,2703
S4	0,0822	-0,0366	-0,7023	0,0515	-1,4432
S5	0,3988	1,2374	-1,3846	0,8652	-0,0176
S6	3,0467	2,5342	-0,1346	-0,1637	1,0399
S7	-1,0722	-2,5680	1,8877	-2,0717	0,9921
S8	1,2253	-0,2031	0,1072	1,6161	-1,1390
S9	-1,9291	1,0513	1,7979	0,4111	-0,1254

Продол^ение таблицы 3

1	2	3	4	5	6
S10	0,7346	-0,6815	0,0776	0,7310	1,0358
S11	-4,7201	-1,2123	-3,4890	-1,1841	-0,2312
S12	-2,0774	2,3232	-0,1217	0,9292	-0,9075
S13	-1,9087	2,6475	0,2270	0,1943	-0,2768
S14	-1,1012	0,7815	1,5129	-0,9098	-1,2679
S15	2,7202	-1,9968	-1,2353	0,4264	-0,7262
S16	1,3055	-3,0790	-0,5480	-0,5233	-0,0975
S17	0,3030	-2,7841	-0,2494	0,3547	0,6062
S18	-0,1928	-1,9659	1,2720	0,0671	-0,1857
S19	-0,2977	-0,5587	1,5653	-0,8495	0,4762
S20	1,7607	0,6096	-1,6640	-3,0627	0,4969
S21	-0,3011	0,6412	1,5472	-0,2990	0,0987
S22	-3,3214	2,0661	0,2432	0,0427	0,3435
S23	-0,1273	-1,6432	1,5546	0,3481	-0,3901
S24	4,3928	1,9483	1,1028	-2,4048	0,4709
S25	-3,5950	0,6885	-0,8321	-1,0896	-0,6842
S26	-2,0855	2,3470	1,0135	-0,7987	1,2144
S27	-0,4039	-1,5900	-2,8914	0,1690	1,4622
S28	2,1337	-0,8767	0,5135	0,0643	-0,3410
S29	0,3876	-1,6309	0,5155	1,1436	-0,7157
S30	-0,9568	-2,1123	1,2492	0,7628	1,2641
S31	0,6803	-1,7561	0,8452	0,7877	0,2204
S32	3,3858	1,0426	0,9819	-2,4790	-1,7056
S33	-0,1936	0,8544	-2,3948	-0,9196	-0,9242
S34	-1,4625	1,9496	1,1392	-0,4509	-0,3033
S35	-0,5848	1,3640	-1,3098	2,0312	-1,6296
S36	2,6333	2,6706	-0,5771	1,4538	-0,1831
S37	-0,6094	-0,5660	2,0993	-0,7058	1,0090
S38	0,3364	0,5397	1,5801	-0,2206	0,3868
S39	-1,6295	-0,1333	1,4686	-0,3302	-0,4854
S40	1,7868	-0,8156	-1,0319	2,0183	1,6526
S41	3,4198	2,2887	-0,5220	0,5294	1,9636
S42	0,2995	-1,4849	0,0358	1,0223	0,8668
S43	0,6624	0,2089	1,0905	0,2311	0,6784
S44	-1,6702	-1,6518	0,3436	-0,4382	-1,9893
S45	0,8911	-1,1680	-0,2239	0,8777	-0,7182
S46	-4,2250	-0,8169	-1,6727	-2,1235	-0,3829
S47	-2,2339	0,3193	-0,5284	0,3658	2,0462
S48	-1,7766	1,5480	-1,2619	0,5668	2,3292
S49	-0,6495	-1,6092	-1,7863	0,5280	0,2862
S50	1,9484	-0,8241	0,2043	0,8191	-1,8913
Координаты опорных точек
MAX	5,7261	2,6623	-0,5752	0,2350	3,4821
MED	-0,1013	-0,5743	0,1045	0,3304	0,4148
MIN	-5,8490	-1,8475	-1,5146	-1,8320	-3,4281

Рассчитав согласно (4) значения D_i ^max , D_i ^med , D_i ^min и сравнив их ме^ду собой, мы увидим кластеризацию выборки оцениваемых ^ивотных по введенным нами условным группам: «Голова», «Ядро» и «Хвост». Это подтвер^дает и рассчитанный согласно (5) комплексный показатель продуктивности ( KP i ).

Результаты расчета комплексного показателя продуктивности иллюстрирует рисунок 3. На рисунке 3 красными ромбами представлены значения KP для ^ивотных, которых условно мо^но отнести к группе «Голова». Это ^ивотные с номерами: S2, S6, S24 и S41. Синими квадратами обозначены значения KP для ^ивотных, которых условно мо^но отнести к группе «Хвост». Это ^ивотные с номерами: S11 и S46. Остальные ^ивотные, значения КР которых обозначены зелеными кру^ками, принадле^ат к группе «Ядро». При этом числовые значения комплексного показателя продуктивности позволяют провести ран^ирование ^ивотных.

0.4

Comprehensive productivity indicator

0.35

♦ Head

• Core ■ Tail

0.3

0.25

CL

0.2

0.15

0.1

0.05

10      15      20      25      30      35      40      45      50

Number of enimals, S

Рисунок 3 – Значения комплексного показателя продуктивности ( KP ) для выборки оцениваемых ^ивотных

Таким образом, полученный комплексный показатель продуктивности ^ивотных позволил провести ран^ирование и оценку ^ивотных одновременно по 15-ти хозяйственно полезным признакам. Полученные результаты позволяют выявить ^ивотных, чьи значения ХПП «выбиваются» в ту или иную сторону от «Ядра». Это дает возмо^ность дальнейшего более детального исследования причин такого «выбивания».

Выво^ы. Представленный алгоритм формирования комплексного показателя продуктивности ^ивотных позволяет провести оценку ^ивотных одновременно по нескольким хозяйственно полезным признакам и пригоден для использования при поиске геномных ассоциаций с фенотипом. При этом такая оценка не накладывает существенных ограничений на количество используемых признаков, однако позволяет выявить наиболее значимые при формировании мясной продуктивности. Учет в расчетах комплексного показателя только главных компонент, полученных с помощью метода РС^, позволяет существенно сократить размерность исходных переменных. При этом значения хозяйственно полезных признаков не теряются, так как все они учитываются в линейной комбинации при построении главных компонент.

Применение подобной методики сопря^ено с достаточно сло^ными математическими вычислениями и требует применения средств компьютерной математики. В настоящее время это не является проблемой в силу широкого распространения таких средств.

Считаем, что использование такого подхода к оценке ^ивотных мо^ет заинтересовать исследователей и специалистов-селекционеров.