Использование концепции стоимостной массы риска при составлении инвестиционных портфелей

Эффективная работа на финансовом рынке требует применения адекватных инструментов оценки рисков, что, в свою очередь, требует наличия специализированных инструментов моделирования доходности и волатильности. В настоящее время доминирующей точкой зрения на эту проблематику является гипотеза о слабой возможности предсказывать доходность финансовых активов, предлагается рассматривать изменения доходности как процесс «случайного блуждания» [8]. С другой стороны, исследования динамики волатильности рыночных активов позволяют строить достаточно успешные модели для прогнозирования волатильности, что является важным фактором для оценки рисков, их контроля и управления ими [6].

Доходность финансового актива rt (здесь и далее рассматривается логарифмическая доходность, rt = ln—^—, где {P} - стоимость финансового актива) рассматривается как случайная величина (вре-L pt-i менной ряд):

ГРНТИ 06.77.65

Сергей Александрович Бандурко – аспирант кафедры банков, финансовых рынков и страхования Санкт-Петербургского государственного экономического университета.

V t =P t + 4t, ^ t = CT_t^E t ,{E t }~Hd(0,1), где t - временная точка (день), ^_t — условное математическое ожидание доходности, ^_t — волатильность, σ t ² – дисперсия волатильности, ɛ t – случайная величина, стандартизированная ошибка.

Доходность, как было сказано выше, слабо поддается прогнозированию, и практика показывает, что ее математическое ожидание незначительно отличается от нуля, поэтому редко моделируется и часто принимается равным 0. Ряд {η t } рассматривается как процесс с нулевым матожиданием и изменяющейся дисперсией σ t ² (гетероскедастичный процесс) [8]. Оценка дисперсии волатильности является крайне важной для стоимостной оценки риска VaR – наиболее известного и распространенного показателя риска для финансовых вложений. Более того, этот показатель является обязательным согласно требованиям Базельского комитета по банковскому надзору (Базель III) [14]. VaR является квантилем уровня 1- p, найденным из распределения прогнозируемой волатильности.

Таким образом, VaR – это значение доходности, ниже которого данная доходность не упадет с вероятностью p [8]. Значение VaR вычисляется исходя из оценки дисперсии волатильности (σ t ²) с учетом выбранного закона распределения стандартизированной ошибки F ɛ :

VaRp = а^РЕ~1(1-р).

Следовательно, если модель адекватно интерпретирует данные, то вероятность пробоя VaR должна составлять (1 – p ).

Основным способом предсказания волатильности является анализ исторических данных об изменении доходности актива за некоторый предшествующий период [11]. Следует отметить, что предположение о возможности прогнозирования состояния системы базируется на концепции «эффективного рынка», которая предполагает, что рыночная цена материальных активов адекватно отображает их реальную стоимость [4]. Однако практика показывает, что данный принцип соблюдается не всегда.

В рамках исследования информационного риска в системе банковских рисков автором были выделены внешние информационные факторы, оказывающие влияние на рыночный риск для инвестора [1]. Был сделан вывод о том, что следующие информационные факторы и особенности поведения рынка неизбежно искажают реальную стоимость актива: манипулирование рынком, приостановка торгов, разрыв цен на рынке, «переполненные» торги (являются следствием того, что трейдеры получают одни и те же сигналы с рынков и часто применяют одинаковые торговые стратегии) [7].

К этим же факторам можно добавить и календарные аномалии, т.е. эффекты, проявляющиеся в аномальном поведении цен в зависимости от временной, календарной и/или сезонной составляющей. Это – «эффект месяца года», «эффект дня недели», «эффект предпраздничных и праздничных дней», «эффект выходного дня», «эффект начала года» (и месяца), «эффект середины месяца», «эффект полудня», «эффект полнолуния», «эффект времени года» [9]. Все вышеперечисленные и другие неупомянутые факторы, а также экстраординарные информационные события вносят свой вклад в колебание волатильности и значительно усложняют финансовое прогнозирование, основанное на интерпретации исторических данных и, безусловно, снижают предсказательную способность модели [2].

Для адекватной оценки риска финансовых вложений автор предлагает использовать концепцию «стоимостной массы риска» (MaR) [5, с. 29-30], которая предполагает разделение стоимостной оценки риска на «реальную» и «виртуальную» составляющие. В отношении оценки риска для финансовых вложений автор предлагает использовать две модели и разделять риск на реальную составляющую, которая соответствует точной модели, и на виртуальную составляющую, которая соответствует осторожной модели. Использование двойного показателя оценки риска позволяет в значительной степени учитывать влияние экстраординарных информационных событий на рынке, влияющих на стоимость активов [6].

Данный подход может быть адаптирован для разных моделей, применяемых для прогнозирования дисперсии волатильности. В настоящей работе автор предлагает подход, основанный на использовании авторегрессионной модели GARCH [12, с. 307-327] (точная модель) и простой регрессионной модели (осторожная модель).

Оценка стоимостной массы риска (MaR) с использованием регрессионной и авторегрессионной (GARCH) моделей для рыночных рисков

Стоимостная масса риска (MaR) в случае оценки рисков для финансовых вложений – это предполагаемые потери в стоимости актива при самом неблагоприятном стечении обстоятельств. Оценку MaR предлагается проводить исходя из поведения актива, наблюдаемого в стрессовые для него периоды, т.е. периоды, в которые доходность актива опускается ниже («пробивает») значения оценки риска (VaR). Таким образом, оценка стоимостной массы риска MaR находится в непосредственной зависимости от оценки риска (VaR) и разделяется показателем VaR на две составляющие: «реальную» – потери, наступление которых имеет существенную вероятность, и «виртуальную» – потери, наступление которых менее вероятно:

MaR = MaR + MaR.

MaR следует рассматривать как оценку «потенциала падения» доходности в период шоковых колебаний. MaR можно сравнить с отметкой уровня воды, которая показывает, до какого значения потенциально может дойти уровень в случае наводнения. MaR и его составляющие, как и VaR, являются характеристиками распределений случайных величин, которые моделируют изменение волатильности. Более конкретно, для уровня значимости p , это квантиль уровня 1 – p . Таким образом, для расчёта MaR требуется: (1) сделать предположение о законе распределения стандартизированной ошибки (ɛ t ) и (2) спрогнозировать значение дисперсии волатильности (σ t ²).

В качестве стандартизированной ошибки в наиболее простых моделях используется стандартное нормальное распределение. В других случаях автор предлагает использовать распределения с нетривиальными скошенностью и куртозисом [10, с. 69-82]. Для прогноза значения дисперсии волатильности на основе исторических данных используется формула:

O? = « 0 + 2 ^^i « i •T t-t² + 2 ; ₌ 1 & TOt-j² .

Значения p и q определяют ретроспективность модели (как правило, p=1 и q=1 уже дают удовлетворительную аппроксимацию). Различные методы моделирования отличаются способами нахождения коэффициентов {α} и {β} и, соответственно, целевой функцией.

Как уже было сказано, для оценки стоимостной массы риска MaR требуется наличие модели для оценки риска (VaR), которая будет наилучшим образом приближаться к реальным данным. Вычисляемое таким методом значение рассматривается как «реальная» составляющая MaR:

MaR~VaR.

На данный момент для расчета оценки риска наибольшее распространение получили авторегрессионные гетероскедастичные модели прогнозирования (GARCH, Generalized AutoRegressive Conditional Heteroscedasticity), которые показывают высокую эффективность и имеют множество модификаций [10, с. 69-82]. Прогнозируемое значение дисперсии рассчитывается по вышеприведенной формуле, коэффициенты определяются методом максимального правдоподобия на основе предшествующих значений в некотором временном интервале L (тайм-фрейм).

Функция правдоподобия для GARCH-модели имеет вид:

max (F(K}, {^;}|{гг})) = 2f=i In ^^2= - 2^5).

Для точной модели размер окна L не может быть слишком большим, так как для значений доходности и волатильности практически всегда наблюдается сильная кластеризация по периодам. В случае использования большого окна, вычисляемые значения дисперсии будут «испорчены» старыми данными. Модель будет завышать риски при входе в «спокойный» период и не сможет достаточно быстро реагировать на шоковые колебания.

После выбора метода для оценки риска появляется возможность определения точек, в которых происходит пробой оценки риска («реальной» составляющей MaR). Наблюдаемые в точках пробоя значения доходности и предшествующие им значения доходности и дисперсии волатильности (исходя из параметров модели p и q ) используются для построения регрессионной модели. Значения доходности и дисперсии волатильности, предшествующие пробою, рассматриваются как независимые переменные модели. Значение дисперсии на момент пробоя рассматривается как зависимая переменная и ее оценка определяется исходя из действительного значения доходности, подразумевая, что это значение доходности есть истинное значение VaR.

Таким образом, значение зависимой переменной дисперсии доходности на временную точку t (σ t ²) рассчитывается как:

= ЫН2,

Vf£ (1-p)/

где r_t – действительное значение доходности на период t ; F – квантиль стандартизированной ошибки.

Для нахождения коэффициентов {α} и {β} можно использовать метод наименьших квадратов. Значение виртуальной составляющей MaR можно определить как разницу между значениями MaR и MaR.

Тестирование

Для тестирования модели были использованы данные котировок акций на Московской бирже (см. таблицу) [13]. Для расчета прогнозируемого значения дисперсии волатильности использовали модель с ретроспективностью p=1, q=2. Для расчета дисперсии MaR – авторегрессионную модель GARCH, для расчета дисперсии MaR – регрессионную модель. В качестве стандартной ошибки – нормальное стандартное распределение, уровень значимости p=0,95. Расчет доходности осуществлялся исходя из стоимости актива на момент закрытия торгов (CLOSE) за день.

Таблица

Применение концепции Стоимостной Массы Риска (MaR) для оценки рисков на основе авторегрессионной и регрессионной моделей

Актив	Временной период	Количество пробоев MaR	Количество пробоев MaR
AKRN	20061020 - 20170714, 2678 кол-во торг. дней	122	30
DIXY	20070626 - 20170714, 2477 кол-во торг. дней	125	25
GAZP	20060123 - 20170714, 2868 кол-во торг. дней	144	39
KMAZ	20050209 - 20170714, 3091 кол-во торг. дней	124	28
LSRG	20071130 - 20170714, 2277 кол-во торг. дней	103	8
MAGN	20060118 - 20170714, 2870 кол-во торг. дней	141	40
MTSS	20031015 - 20170714, 3412 кол-во торг. дней	159	46
MVID	20071106 - 20170714, 2409 кол-во торг. дней	95	18
NLMK	20060418 - 20170714, 2808 кол-во торг. дней	133	20
VSMO	20050302 - 20170714, 2961 кол-во торг. дней	129	31
VTBR	20070528 - 20170714, 2534 кол-во торг. дней	133	29

Моделирование проводили в течение периода в несколько дней, определяя коэффициенты дисперсии волатильности для каждого дня, с использованием значений в предшествующем тайм-фрейме, который составлял 50 дней. Проводили подсчет количества случаев, когда значение логарифмической доходности актива опускалось ниже значений оценок риска MaR и MaR (пробой оценки). Результаты представлены в таблице.

Использование Стоимостной Массы Риска для оценки возможных потерь при финансовых вложениях на основе нескольких случайно выбранных активов показывает возможность учесть 75-80% случаев пробоев критических значений доходности актива (VaR), которые определяются с использованием метода GARCH. На рисунке приведены изменения доходности VTBR и оценок рисков в период второго полугодия 2014 г., характеризующегося значительной турбулентностью на российском финансовом рынке.

Оценка риска с использованием показателя MaR показывает себя состоятельной, пробои MaR остаются в рамках заданного уровня значимости ( p =0.95). В то же время, в указанный период пробой MaR наблюдается один раз и значение оценки приближено к действительному значению доходности. Необходимо отметить, что преимущество использования Стоимостной Массы Риска (MaR) при составлении инвестиционного портфеля заключается в комплексном учете двух показателей оценки риска MaR и MaR.

Заключение

На основании вышеизложенного, можно сделать вывод, что использование концепции Стоимостной Массы Риска (MaR) с применением двойного показателя оценки риска, основанного на прогнозировании волатильности, может быть рекомендовано для учета колебаний доходности актива, которые выходят за пределы выбранного доверительного интервала модели и в значительной степени вызваны экстраординарными событиями на рынке. Для прогноза значения волатильности был использован метод моделирования GARCH(1,2) и регрессионный анализ. Преимущество при менения данной концепции подтверждается тем, что Стоимостная Масса Риска (MaR) позволила учесть 75-80% случаев пробоя VaR.

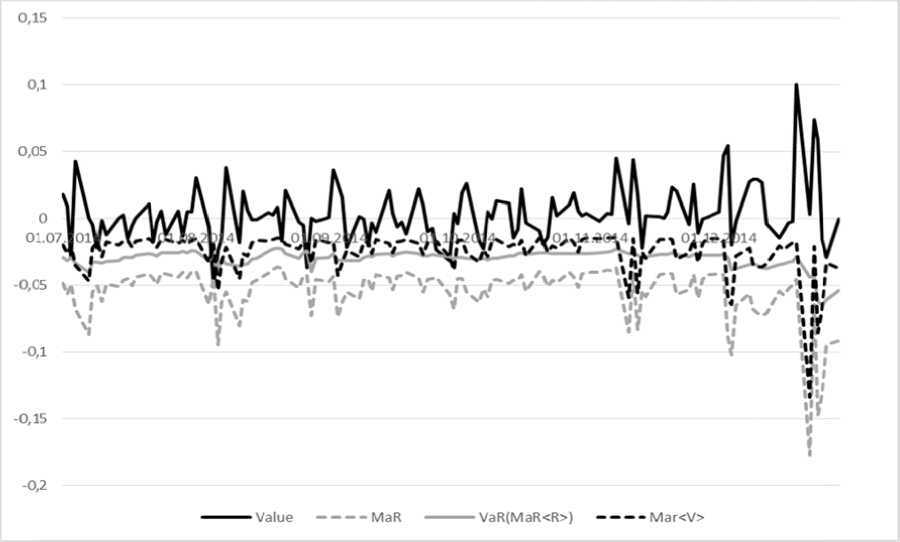
Рис. Измен е ние доходн о сти ВТБ во в тором полу г одии 2014 г о да

Данный подход к анализу р и сков може т быть исп о льзован с различными методам м о делирования волатиль н ости и может быть ра з вит в даль н ейшем для повышени я точности п рогнозов. С огласно концепции, которая в настоящее в р емя разви в ается авто р ом в отде л ьном науч н ом исслед о вании, такие события я вляются частью информационно г о риска, я в ляющегос я поправоч н ым риском и оказывающим вли я ние на другие финанс о вые риски. Таким образом, предл о женный п о дход к оце н ке риска при составлении инвестиционного портфеля д о полняет концепцию и нформаци о нного рис к а как поправочного риска.