Использование корреляционных методов для обработки данных с волоконно-оптических брэгговских датчиков и анализ возможных ошибок этих методов

Сфера применения контрольно-измерительных комплексов на основе волоконнооптических брэгговских датчиков [1] в настоящее время стремительно расширяется. Можно отметить, что одной из весьма перспективных областей применения таких датчиков является авиационно-космическая техника [2]. Новые области применения волоконнооптических брэгговских датчиков делают ещё более актуальной задачу повышения точности таких измерений.

Как уже отмечалось в работе [3], одной из важнейших проблем является повышение точности определения положения брэгговского пика в спектре. При этом интерес представляет не столько абсолютное значение положения пика, сколько смещение пика относительно некоторого начального положения, например, относительно положения данного пика до начала воздействия на брэгговский датчик. В связи с этим в дальнейшем в данной работе будет использоваться термин опорный спектр , под которым будет пониматься оптический спектр с брэгговского датчика, полученный в начале эксперимента и используемый в последующем при корреляционных расчётах.

Одним из основных факторов, ограничивающим точность определения смещения брэгговских пиков (и, как следствие, ограничивающим точность измерений, выполняемых с помощью волоконно-оптических брэгговских датчиков) является зашумлённость брэгговских спектров. Наряду с методом гауссовской аппроксимации брэгговских пиков [3], эффективным средством снижения влияния шума на результат измерений и повышения их точности могут служить корреляционные методы обработки экспериментальных данных.

К настоящему времени уже имеется ряд публикаций (например, работа [4]), посвящённых корреляционным методам расчёта смещения брэгговских пиков. Однако, вопросы, связанные с этими расчётами, далеко ещё не являются полностью выясненными. В, частности, изучения требует вопрос о таких ошибках используемых методов, которые вызываются реакцией метода счёта на дискретность фоточувствительного прибора и в случае узких брэгговских пиков могут быть весьма существенными.

Как уже отмечалось в работе [3], такие ошибки методов обработки данных могут приводить к тому, что после обработки экспериментальных данных в поведении исследуемой с помощью брэгговского датчика физической величины могут быть обнаружены некоторые осцилляции, которые в действи- тельности отсутствуют. Поэтому способность того или иного метода обеспечить достаточно малые ошибки является столь же важным критерием, как и способность данного метода противостоять шуму в брэгговском спектре.

Общее описание принципа корреляционного метода определения смещения брэгговского пика

В несколько упрощённом виде задача корреляционной обработки брэгговского спектра может быть сформулирована как задача отыскания для каждого брэгговского пика такого значения сдвига 5 = sm, при котором максимально значение интеграла x 2

B ( s ) = J E r ( X — 5 ) E s ( X ) dx ,     (1)

X 1

где E(x - s) и E(x) - распределения освещённостей в опорном и сдвинутом спектрах, рассматриваемые как функции координаты, измеренной вдоль линейки светочувствительных пикселей, на которые проецируются эти спектры; x 1 и x₂ представляют собой границы той зоны сдвинутого спектра, в которой находится данный брэгговский пик. При этом в качестве координаты удобно использовать безразмерную величину, считая, что значение, равное i , эта безразмерная координата принимает в центре i -ого пикселя. Особо необходимо оговорить, что хотя номер пикселя является целочисленной величиной, эта безразмерная координата является величиной непрерывной. Непрерывными являются и функции E_r(x - s) и E_s(x) .

Однако, при реальных расчётах придётся оперировать не с непрерывными функциями E_r(x - s) и E_s(x) , а с дискретными величинами - с наборами значений сигналов опорного и сдвинутого спектров, получаемых с пикселей ПЗС-линейки. В этом случае выражение для функции B(s) превратится из интеграла в сумму:

i 2

B ^{( 5} ) = Z U r ⁽ x i ^- 5 ) U s ⁽ x i )•     ⁽²⁾

i = i i

Здесь us(x) - амплитуда сигнала сдвину того спектра, полученная с i-ого пикселя, i1 и i2 - номера первого и последнего пикселей ПЗС-линейки, на которые проецируется изображение данного брэгговского пика в сдвинутом спектре. Вопрос об определении этих номеров является достаточно важным и в дальнейшем он ещё будет затронут.

Функция u_s(x) представляет собой дискретную функцию - она определена только для целочисленных значений аргумента, то есть для каждого из номеров пикселей, с которых была получена информация о брэгговском пике в сдвинутом спектре. Таким образом, набор значений амплитуд сигналов, получаемых в эксперименте с каждого из представляющих интерес пикселей ПЗС-линейки, и будет тем набором значений функции u₅(x_i) , который необходимо использовать при расчёте.

А вот с функцией u r (x_i - s) , описывающей брэгговский пик в опорном спектре, возникает проблема. Поскольку сдвиг пика s не обязательно является целочисленной величиной, функция u_r(x. - s) должна быть задана как непрерывная функция. В то же время информация об опорном спектре представляет собой дискретный набор значений - точно так же, как и информация о сдвинутом спектре.

Прежде, чем рассмотреть пути решения этой проблемы, необходимо сделать несколько замечаний.

Во-первых, отметим, что функция B(s) с точностью до коэффициента (зависящего от i₁ и i₂ и фиксированного после выбора i₁ и i 2 ) представляет собой корреляционную функцию.

Во-вторых, во всех дальнейших расчётах, а так же при численном моделировании, будет использовано предположение, что регулярная (то есть за вычетом шумовой компоненты) составляющая брэгговского пика имеет одинаковую или, по крайней мере, почти одинаковую форму как в опорном, так и в сдвинутом спектре. Уточним, что речь здесь идёт о форме именно брэгговского пика, то есть о форме распределения освещённости вдоль линейки светочувствительных пикселей (если строго - о форме регулярной составляющей этого распределения), а не о виде гистограммы, изображающей амплитуды сигналов. Предположение о том, что форма брэгговского пика не меняется при его смещении вдоль линейки светочувствительных пикселей, по-видимому, достаточно адекватно соответствует реальной ситуации в большинстве практически важных случаев.

Третье замечание касается способа поиска точки максимума функции B(s) при практических расчётах. Поскольку вблизи значения s_m функция B(s) имеет только один максимум (исключение могут составить только чрезвычайно сильно зашумлённые спектры, вряд ли представляющие практический интерес), то задача поиска точки максимума функции B(s) полностью эквивалентна задаче поиска нуля её производной, то есть решению уравнения

ref (x) = ∂ur . ∂x

∂ B _=0. ∂ s

Задача поиска нуля производной с вычислительной точки зрения более удобна, чем задача прямого поиска максимума функции.

Производная функции B(s) может быть вычислена как

∂ B

∂ S

-

i 2

∑ i =i1

∂ u_r ∂ x

^⋅ u s ( x i ) . (4) x = x _i - s

Таким образом, для решения задачи определения сдвига брэгговского пика необходимо решение уравнения

^{i 2} ∂ u

∑                 ⋅ us(xi) = 0,    (5)

i = i 1 ^{∂ x} x ⁼ x i ^- s

∂ur где r ‒ производная опорного сигнала по ∂x координате, измеренной вдоль ПЗС-линейки. А так как значение сдвига s не обязательно является целым числом, эта производная, как и сама функция ur в формуле (2), должна быть непрерывной функцией координаты. Однако, как уже отмечалось, информация об опорном спектре дискретна.

Прежде, чем вернуться к обсуждению этой проблемы, введём обозначение

и отметим, что функция ref(x) ‒ некоторая непрерывная функция, которая несёт информацию об опорном спектре, а точнее, о производной опорного спектра по координате. Для функции ref(x) в дальнейшем будет использован термин опорная функция .

Для краткости переменная x будет использована здесь и далее для обозначения аргумента функции ref , но необходимо помнить, что при расчётах по формуле (5) в качестве аргумента функции ref должна быть подставлена величина x = x_i ‒ s .

Итак, теперь можно отметить, что вопрос о том, как от дискретного набора значений опорного спектра u_r(x_i) перейти к непрерывной опорной функции ref(x) и является вопросом о выборе того или иного варианта корреляционного метода.

Что же касается выбора пределов суммирования, то есть выбора точек сдвинутого спектра для участия в процедурах корреляционных расчетов, то здесь можно отметить следующее. Для участия в процедурах гауссовской аппроксимации, которые подробно рассмотрены в работе [3], выбирались те точки пика в опорном спектре, которые лежат в интервале от 10 до 100% высоты данного пика. Для участия в процедурах корреляционных расчетов могли быть выбраны либо только такие же точки в сдвинутом пике, либо дополнительно к этим точкам могло быть использовано по несколько дополнительных точек с каждой стороны пика. Как будет показано далее, включение достаточного числа дополнительных точек (то есть точек на “крыльях” пика) является необходимым условием для получения до статочно малой ошибки расчёта сдвига пика (ошибки метода).

Возможные варианты корреляционного метода определения смещения брэгговского пика

Одним из простейших вариантов применения корреляционного метода для обработки брэгговских спектров будет вычисление разности значений амплитуд сигнала между

соседними точками спектра (то есть получение дискретного набора значений производной опорного спектра по координате) и использование линейной интерполяции для нахождения значений опорной функции ref(x) в “промежуточных” точках.

Для реализации этого метода для каждого целого числа i в пределах от 1 до N ‒ 1, где N ‒ общее число светочувствительных пикселей, с которых получены данные об опорном спектре, определим A u_t как

Au = ur (xM) - ur (x). (7)

Далее значение опорной функции для любого (в том числе и не целочисленного) значения координаты x из интервала от 1 до N ‒ 1 может быть вычислено путём линейной интерполяции:

ref (x) = Au i + (Aui+1 - Aui)(x - 0,5 - i), (8)

где = trunc ( x ‒ 0,5) ‒ целая часть числа ( x ‒ 0,5). Сдвиг 0,5 необходим потому, что при вычислении коэффициентов интерполяции по формуле (7) значение A u i имеет смысл производной, вычисленной в точке, расположенной приблизительно посередине между пикселями с номерами и + 1.

Такой вариант корреляционного метода является традиционным и весьма удобным в реализации, но ему присущ серьёзный недостаток: в том случае, если брэгговский пик достаточно узок (как часто и бывает в реальных экспериментах), такой способ построения опорной функции может привести к появлению специфической и достаточно большой ошибки в определении смещения пика. Если же устранить вызванные применением линейной интерполяции ошибки в вычислении опорной функции, то исчезнет и соответствующая ошибка в определении смещения пика.

Эта задача может быть решена с помощью аппроксимации каждого из пиков в опорном спектре какой-либо функцией, которую можно задать в виде аналитиче ского выражения, содержащего координату (как аргумент функции) и некоторые параметры (которые должны быть определены при аппроксимации). Затем для каждого из пиков в опорном спектре должна быть вычислена производная по координате от соответствующей данному пику аппроксимирующей функции. Эта производная, которая также будет задана в виде некоторого аналитического выражения, и будет использована в качестве опорной функции.

В качестве аппроксимирующей функции естественным представляется выбрать функцию Гаусса, так как брэгговские пики, как правило, достаточно хорошо описываются гауссовским распределением. Следует, однако, заметить, что иногда (например, из-за не-идеальности брэгговской структуры) отклонения от гауссовской формы могут оказаться весьма существенными. В связи с этим представляет интерес, к каким результатам приведёт попытка применить гауссовскую аппроксимацию для брэгговского пика явно негауссовской формы.

Наиболее простым и в то же время наиболее адекватным способом получить ответ на этот вопрос представляется проведение моделирования пиков различной формы и проведение соответствующих расчётов для модельных пиков.

В качестве модельных пиков использовались гауссовский и “деформированный” пики с такими же параметрами, как и в работе [3]. И, как показало моделирование, применение гауссовской аппроксимации к негауссовским пикам является вполне допустимым. Как бы это не казалось странным на первый взгляд, гауссовская аппроксимация негауссовского пика даже не приводит к появлению принципиально неустранимых ошибок метода ‒ для сохранения точности на том же уровне, что и для гауссовского пика, необходимо всего лишь несколько увеличить число включаемых в расчёт дополнительных точек.

Результаты моделирования для корреляционного метода с линейной интерполяцией опорной функции

Результаты моделирования для гауссовского брэгговского пика с параметром о = 1,5 пикселя представлены на рис.1. При отсутствии дополнительных точек наблюдаются

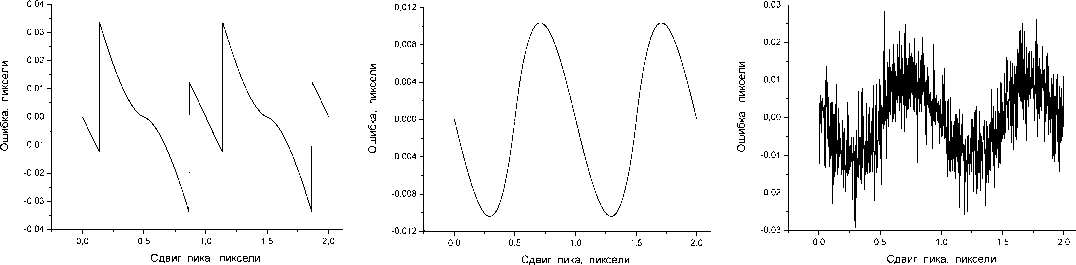
а)                                    б)                                     в)

Рис.1. Результаты моделирования для корреляционного метода с линейной интерполяцией опорной функции: а ě ошибка метода в случае, если дополнительные точки не используются, б ě ошибка метода в случае, если используется по пять дополнительных точек с каждой стороны пика, в ě выходной шум в случае, если используется по пять дополнительных точек с каждой стороны пика, среднеквадратическое значение входного шума 0,5% от амплитуды брэгговского пика: даже на фоне шумовой ошибки ясно просматривается периодическая по координате и весьма значительная ошибка метода

значительные ошибки и внезапные изменения этой ошибки (так называемые “прыжки”), появляющиеся в момент изменения набора используемых для расчёта точек (такие изменения происходят по мере движения брэгговского пика вдоль линейки светочувствительных пикселей): рис.1а. Включение в расчёт дополнительных точек позволяет устранить “прыжки” и всего лишь в несколько раз уменьшить ширину полосы ошибки (рис.1б). Особая неприятность состоит в том, что хотя при включении первых дополнительных точек ошибка данного варианта корреляционного метода уменьшается, при дальнейшем увеличении числа дополнительных точек ширина полосы ошибки стремится к некоторому постоянному значению.

Практически единственным преимуществом, которое данный вариант корреляционного метода имеет перед центроид-методом, оказывается его реакция на входной шум. При использовании данного метода выходной шум (рис.1в) оказывается примерно в три раза ниже, чем выходной шум центроид-метода при таких же параметрах входного сигнала и использовании трёх дополнительных точек с каждой стороны пика [3]. Кроме того, величина выходного шума корреляционного метода практически не возрастает при увеличении числа участвующих в корреляционных расчётах дополнительных точек.

Результаты моделирования для пика негауссовской формы дают аналогичные ре- зультаты; с той лишь разницей, что для показанного на рис.3а негауссовского пика выходной шум уменьшается не столь заметно: выигрыш по сравнению с центроид-методом составляет около двух раз.

Результаты моделирования для корреляционного метода с гауссовской аппроксимацией пиков опорного спектра

Рассмотрим результаты моделирования, произведённого по этому методу ‒ сначала для брэгговского пика гауссовской формы с параметром о = 1,5 пикселя.

При отсутствии дополнительных точек этот вариант корреляционного метода также даёт достаточно большие ошибки (рис.2а). Однако в отличие от корреляционного метода с линейной интерполяцией опорной функции, рассматриваемый здесь корреляционный метод с гауссовской аппроксимацией пиков опорного спектра характеризуется быстрым уменьшением ошибки метода при увеличении числа дополнительных точек. Так, например, при трёх дополнительных точках с каждой стороны пика ширина полосы ошибки данного метода составляет менее 10-4 пикселя, при пяти дополнительных точках ‒ менее 10-7 пикселя (рис.2б), что на несколько порядков ниже уровня выходного шума. Таким образом, при включении в расчёт достаточного числа дополнительных точек ошиб-

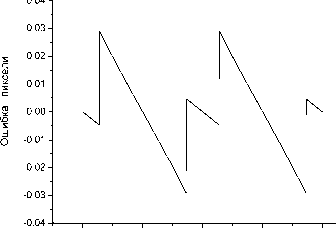
0,0             0,5             1,0             1,5             2,0

Сдвиг пика, пиксели

а)                                    б)                                     в)

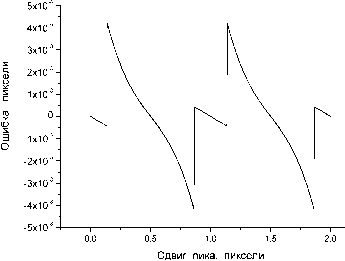
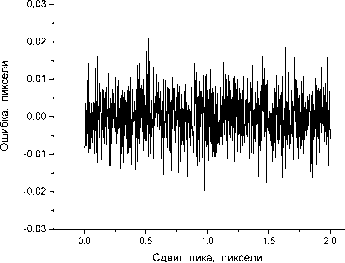
Рис.2. Результаты моделирования для корреляционного метода с гауссовской аппроксимацией опорного сигнала, моделирование для брэгговского пика гауссовской формы: а - ошибка метода в случае, если дополнительные точки не используются, б - ошибка метода в случае, если используется по пять дополнительных точек с каждой стороны пика, в - выходной шум в случае, если используется по пять дополнительных точек с каждой стороны пика, среднеквадратическое значение входного шума 0,5% от амплитуды брэгговского пика: ошибка метода не заметна на фоне шумовой ошибки ка данного варианта корреляционного метода может быть снижена до любого реально необходимого значения.

Устойчивость этого метода к входному шуму в дальнейшем ещё будет рассмотрена, пока же отметим, что для брэгговского пика гауссовской формы ( σ = 1,5 пикселя) данный вариант корреляционного метода обеспечивает приблизительно в три раза меньшее среднеквадратическое значение выходного шума (рис.2в), чем обеспечивает при тех же условиях центроид-метод и использовании трёх дополнительных точек с каждой стороны пика [3].

Теперь рассмотрим применение данного варианта корреляционного метода к брэгговскому пику негауссовской формы.

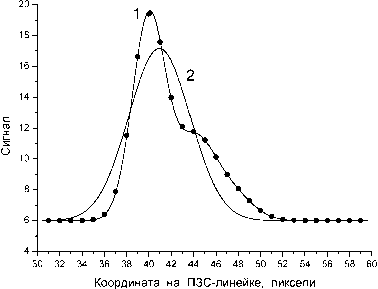
На рис.3а показан пример аппроксимации такого пика гауссовской кривой. Очевидно, что такая аппроксимация не является “хорошей” в том смысле, что она выполнена с существенно большей величиной Q (формула (2) в работе [3]), чем аналогичная аппроксимация для пика гауссовской формы. Однако, моделирование показывает, что большая величина Q отнюдь не даёт оснований считать гауссовскую аппроксимацию неприемлемой для негауссовского пика.

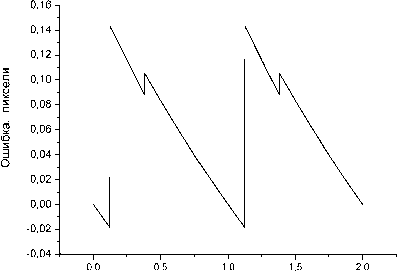
Как и для пика гауссовской формы, при отсутствии дополнительных точек этот вариант корреляционного метода имеет достаточно большую ширину полосы ошибки

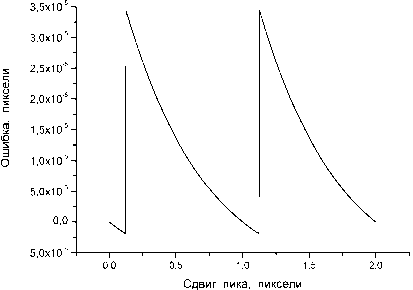
(рис.3б). Однако, ширина полосы ошибки имеет явную тенденцию быстро уменьшаться при увеличении числа дополнительных точек ‒ также, как это наблюдалось и для гауссовского пика. Разница состоит лишь в том, что в расчёт необходимо включать большее число дополнительных точек (вследствие того, что показанный на рис.3а “деформированный” пик имеет более широкие “крылья”). На рис.3в показана ошибка данного метода при восьми дополнительных точках с каждой стороны негауссовского пика ‒ видно, что ширина полосы ошибки не превышает 4 _⋅ 10 ^{- 5} пикселя.

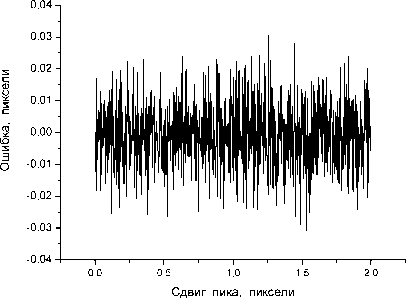
Анализ шумовых свойств данного метода показывает, что для показанного на рис.3а пика этот метод обеспечивает приблизительно вдвое меньшее значение выходного шума (рис.3г), чем центроид-метод при таком же входном шуме и таких же параметрах пика [3].

Итак, вариант корреляционного метода с гауссовской аппроксимацией опорного спектра представляется до статочно перспективным для обработки данных с волоконнооптических брэгговских датчиков. Поэтому представляется интересным подробнее рассмотреть свойства этого метода в применении к брэгговским пикам различной ширины.

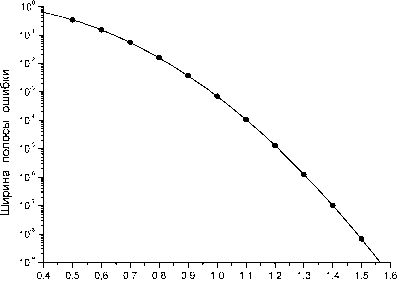
На рис.4а представлена зависимость ширины полосы ошибки данного метода от

а)

Сдвиг пика, пиксели

б)

в)

^{г )}

Рис.3. Пример аппроксимации “деформированного” (негауссовского) опорного пика гауссовской функцией (а): Кривая 1 ě зависимость освещенности ПЗС-линейки от координаты, чёрные точки ě значения сигнала, получаемого с ПЗС линейки, кривая 2 ě гауссовская аппроксимационная кривая. Результаты моделирования: б ě ошибка метода, в случае, если дополнительные точки не используются, в ě ошибка метода, в случае, если используется по восемь дополнительных точек с каждой стороны пика, г ě выходной шум в случае, если используется по восемь дополнительных точек с каждой стороны пика, среднеквадратическое значение входного шума 0,5% от амплитуды брэгговского пика: как и в случае гауссовского пика, ошибка метода незаметна на фоне шумовой ошибки ширины пика (точнее, от параметра о - дисперсии гауссовского распределения). Видно, что для гауссовских пиков с параметром о < 0,8...0,9 пикселя этот метод даёт достаточно большие ошибки. Но при увеличении ширины пика ширина полосы ошибки данного варианта корреляционного метода стремительно уменьшается. Так, уже при о ~ 1,0...1,1 пикселя (что соответствует ширине пика по уровню половины высоты 2,4...2,6 пикселя) ширина полосы ошибки становится существенно меньше уровня шума. Как следствие, можно ожидать, что в большинстве реальных экспериментов ошибка данного варианта корреляционного метода будет на несколько порядков меньше ошибки, обусловленной шумом.

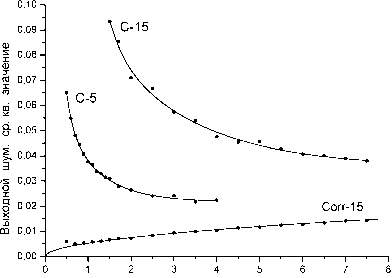
Зависимость шума в выходных данных от ширины брэгговского пика (точнее, как это было сделано ранее для ошибки метода, - от параметра о) показана на рис.4б. Хорошо видно, что по мере увеличения ширины пика выходной шум корреляционного метода растёт пропорционально квадратному корню из этой ширины.

Интересно сопоставить этот факт с приведённым в работе [4] утверждением, что отношение сигнал/шум в выходных данных растёт пропорционально N, , где N - число отсчётов (точек ПЗС-линейки), приходящихся на данный брэгговский пик. На первый взгляд, рис.4б иллюстрирует противоположную тенденцию - падение отношения сигнал/ шум пропорционально V N . Однако, на самом деле это не так. Необходимо отметить, что на рис.4б представлен график зависимости уровня выходного шума, измеренного в

Параметр Sigma

а)

Рис.4. а ě зависимость ошибки корреляционного метода с гауссовской аппроксимацией опорного сигнала от параметра σ (дисперсии гауссовского распределения) брэгговского пика, б ě зависимость выходного шума от параметра σ брэгговского пика. Кривые C-5 и C-15 ě для центроид-метода при 5 и 15 дополнительных точ ках с каждой стороны пика, кривая Corr-15 ě для корреляционного метода при 15 дополнительных точек с каждой стороны пика. Кривая Corr-15 представляет собой кривую типа y ~ x . Во всех случаях моделирование проводилось для пика гауссовской формы. По всем осям использованы безразмерные единицы (пиксели)

Параметр Sigma

б)

долях пикселя, от параметра σ , также измеренного в долях пикселя. Это означает, что если на одну и ту же ПЗС-линейку проецируются два пика ‒ один широкий, а другой узкий, то влияние шума на широкий пик (то есть на пик с менее “острой” вершиной) будет заметнее и, как следствие, точность определения его смещения будет ниже.

Но в работе [4] речь идёт не об уширении пика, а о другой ситуации ‒ о случае, когда два одинаковых брэгговских пика проецируются на две различные по разрешающей способности ПЗС-линейки. В этом случае вторая линейка, имеющая в N раз более высокую разрешающую способность (то есть в N раз большее число пикселей на миллиметр), чем первая, даст в N раз большее значение шума, но ‒ важное замечание ‒ значение шума, измеренное в долях пикселя. Для перехода к значению шума, выраженного в размерных единицах длины, необходимо будет умножить это безразмерное значение шума на пространственный период ПЗС-линейки. Очевидно, что при таком переходе для второй линейки будет получено в N раз меньшее значение шума ‒ в полном соответствии с выводом, приведённым в работе [4].

Интересно отметить, что кривая Corr-15 на рис.4б практически в точности повторяет аналогичную кривую A-15 для метода опре- деления смещения пика с помощью гауссовской аппроксимации (рис. 3б в работе [3]). Этот факт представляется вполне объяснимым, если учесть, что и при минимизации величины Q для метода наименьших квадратов, и при поиске максимума корреляционной функции B(s) выполняются достаточно похожие математические операции.

При выборе числа экспериментальных точек, участвующих в корреляционных расчётах, опасность с точки зрения увеличения выходного шума представляет не “перебор”, а “недобор” дополнительных точек. Как показывает анализ результатов моделирования, при недостаточном числе дополнительных точек и при наличии шума во входном сигнале случайные изменениям набора участвующих в расчёте экспериментальных точек затрагивают те точки, которые вносят достаточно заметный вклад в сумму (5). Это, в свою очередь, резко увеличивает выходной шум. В то же время при избыточном числе участвующих в расчёте точек увеличивается лишь время счёта, но не увеличивается выходной шум. Таким образом, при использовании корреляционного метода задача определения оптимального числа участвующих в расчётах точек стоит существенно менее остро, чем при использовании центроид-метода ‒ при корреляционных расчётах допустимо выбрать число точек с заведомым завышением и это не приведёт к возрастанию уровня выходного шума.

На изменение уровня шума во входном сигнале все методы, рассмотренные в настоящей работе и в работе [3], реагируют линейно ‒ среднеквадратическое значение шума в выходных данных линейно зависит от среднеквадратического значения шума в брэгговском спектре.

Сравнение предсказаний моделированияи экспериментальных результатов

В таблице 1 приведены результаты экспериментов и численного моделирования для шести брэгговских пиков различной ширины. Нормированный входной шум вычислялся как отношение экспериментально полученного среднеквадратического значения шума в области брэгговского пика к амплитуде данного пика. Пересчёт выходного шума из безразмерных единиц в размерные осуществлялся с учётом дисперсии использованного в данных экспериментах полихроматора ‒ 86 пм на пиксель.

Численное моделирование проводилось после завершения экспериментов, причём в качестве значения параметра σ и уровня входного шума были использованы экспериментально полученные значения. Сравнение предсказаний моделирования и результатов экспериментов показывает, что только в одном случае из шести расхождение составляет 26 %, а во всех остальных случаях не превышает 18 %. Для шумового моделирования при отсутствии точной информации о спект- ре и природе входного шума такое совпадение можно считать весьма хорошим результатом.

Здесь необходимо подчеркнуть, что при моделировании устанавливались равными экспериментальным лишь среднеквадратические значения входного шума, но не спектры шумов. В то же время, первые же попытки анализа спектра шума реальных брэгговских спектров показали, что в проведённых экспериментах этот шум имел явно негауссовский характер. Кроме того, уровень шума в области вершины пика оказался несколько выше, чем на “крыльях” пика, то есть шум имел частично мультипликативный характер. При моделировании такой характер шума не воспроизводился, а в качестве значения входного шума в программу вводилось среднеквадратичное значение шума по всей области пика.

И, тем не менее, неучёт этих факторов достаточно слабо сказался на адекватности проведённого моделирования. Если же эти факторы будут учтены при моделировании, то, возможно, это позволит ещё более повысить его адекватность.

Заключение и некоторые выводы

Итак, моделирование и эксперименты показывают, что корреляционный метод с гауссовской аппроксимацией опорного спектра обеспечивает существенно более низкий выходной шум, чем центроид-метод, особенно в случае обработки данных об узких брэгговских пиках.

По устойчивости к входному шуму дан-

Таблица 1. Сравнение предсказаний моделирования и результатов экспериментов

Амплитуда пика, отн. единицы	Sigma пика, пиксели	Нормированный входной шум	Выходной шум, ср.кв. значение в пикометрах
			Моделирование ( m )	Эксперимент ( e )	Отношение (e ‒ m) / m
0,12	4,43	0,019	3,6	3,4	- 5,6 %
0,50	3,63	0,0057	0,97	1,05	8,2 %
0,10	2,64	0,021	3,3	2,7	- 18 %
0,50	1,86	0,0053	0,70	0,71	1,4 %
0,09	1,25	0,021	2,3	2,9	26 %
0,50	0,75	0,0048	0,43	0,50	16 %

ный вариант корреляционного метода имеет такую же эффективность, как и метод определения положения пиков с помощью гауссовской аппроксимации пиков сдвинутого спектра [3]. Однако, данный вариант корреляционного метода может иметь преимущество в части снижения затрат машинного времени, так как при корреляционных расчётах процедура аппроксимации выполняется только один раз (при обработке информации об опорном спектре).

Число дополнительных точек (т.е. точек на “крыльях” пика) при корреляционных расчётах допускается выбирать с явным завышением, не опас аясь увеличения уровня шума в выходных данных.

Корреляционный метод с гауссовской аппроксимацией опорного спектра может быть применим и в случае обработки данных о негауссовских брэгговских пиках.

Простейший вариант корреляционного метода (с использованием линейной интерполяции для нахождения значений опорной функции в “промежуточных” точках) может быть пригоден для анализа брэгговских спектров лишь в том случае, когда разрешающая способность ПЗС-линейки достаточно велика и обеспечивает получение не менее, чем несколько десятков отсчётов на каждый брэг- говский пик.

В том случае, когда необходимо обрабатывать данные об узких брэгговских пиках ( σ ≈ 0,7...0,9 пикселя), предпочтение может быть отдано методу определения положения брэгговских пиков с помощью гауссовской аппроксимации пиков сдвинутого спектра [3].