Использование космической тросовой системы для решения задачи доставки груза на орбиту

Для доставки груза с поверхности Земли на орбиту традиционно используют ракетоносители. В последние десятилетия активно ведутся работы по созданию альтернативных схем доставки с использованием космических тросовых систем. Их главным достоинством является снижение стоимости операции вывода за счёт отказа от использования последней ступени ракетоносителя. В научной литературе обсуждается несколько методов перевода груза на более высокую орбиту, используя КТС [1]. Самым амбициозным и труднореализуемым проектом является космический лифт, представляющий собой расположенную в экваториальной плоскости космическую тросовую систему, соединяющую поверхность Земли с находящейся за геостационарной орбитой космической станцией. Центробежная сила обеспечивает устойчивость этой конструкции. Груз доставляется на орбиту на движущемся вдоль троса подъемнике [2]. Более реальной является концепция космического эскалатора – постоянно находящейся на орбите радиально ориентированной КТС. Спутник выводится на низкую орбиту, где пристыковывается к нижнему концу эскалатора и перетягивается с помощью специального подъемного механизма по тросу наверх. Там он отстыковывается и продолжает свой полет на более высокой орбите[1]. Другим обсуждаемым в научной литературе способом является использование вращающихся вокруг центра масс КТС. Груз выводится на низкую ор-

биту, где стыкуется с нижним концом КТС. Трос обеспечивает передачу энергии и количества движения от находящегося на орбиту спутника выводимому грузу. После того как груз, совершая вращение в рамках КТС, попадает в высшую точку, происходит расстыковка [3].

В данной статье предлагается рассмотреть комбинированный способ выведения груза на орбиту с помощью переводимой во вращение радиально-ориентированной КТС. До момента стыковки космическая тросовая система находится в радиальном положении. С помощью ракетоносителя на орбиту выводится космический аппарат, который пристыковывается к нижнему концу КТС. После этого КТС выводится из устойчивого радиального положения и переводится во вращение. В наивысшей точке происходит отделение КА. Перевод во вращение может осуществляться за счет реактивных, электродинамических и инерциальных сил, а также за счет управления длиной троса. Достоинством этого способа является простота стыковки, поскольку не нужно синхронизировать вращение КТС и орбитального движения КА, а также отсутствие движущегося по тросу подъемника.

В данной работе рассматривается движение КТС с момента стыковки КА до момента его отделения. Перевод во вращение осуществляется за счет разности скоростей стыковочного модуля и выводимого космического аппарата. Стыковка происходит мгновенно и может рассматриваться, как абсолютно неупругий удар.

Целью работы является исследование возможности доставки груза на орбиту с помощью переводимой во вращение радиально-ориентированной космической тросовой системы; разработка математической модели, описывающую динамику КТС после стыковки с выводимым на орбиту КА; определение условий стыковки, обеспечивающих безопасный вывод груза на более высокую орбиту.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

[ ES

c = <

l 0

, если10 < 1,

, если10 > 1,

Рассмотрим тросовую систему, которая состоит из несущего спутника массой M с центром масс в точке C , невесомого упругого троса длиной l и стыковочного модуля с прикрепленным к нему грузом массой m . Спутник движется на орбите радиусом r (рис. 1). Предполагаем, что на систему действует только гравитационная сила. Несущий спутник и груз представляются в виде материальных точек. Рассматривается плоское движение системы. Введем жестко связанную с Землей инерциальную систему координат Oxy .

Составим уравнения Лагранжа 2-ого рода. В качестве обобщенных координат выберем параметры r , l , ф и 0, где 0 - угол истинной аномалии, ф - угол между осью Oy и тросом.

Найдём потенциальную энергию системы. Она складывается из потенциальной энергии несущего спутника, стыковочного модуля и энергии упругой деформации троса:

П=-MM - Mm + 1 c ( - ,0)2, (1)

r rr2 + 2 r1 cos(y) +I2 2

где l ₀ – длина недеформированного троса; c – жесткость троса; M — гравитационный параметр;

п

Y = - - 0 + ф.

Если трос не натянут ( I < I ₀ ) то несущий спутник и стыковочный модуль представляет собой систему из двух свободно движущихся точек. Это явление можно учесть, если рассматривать коэффициент жесткости троса как кусочно-заданную функцию:

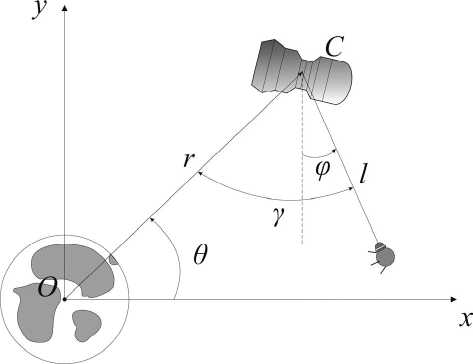
Рис. 1. Космическая тросовая система где E – модуль Юнга, S – площадь поперечного сечения троса.

Найдем кинетическую энергию системы. Она состоит из кинетической энергии несущего спутника и стыковочного модуля.

- 2 r01 sin( Y ) + r ² + 2 1rф sin( y ) + 1 2 ).

Лагранжиан запишется в виде:

L = T - П.

Перепишем (4) учитывая уравнения (1) и (3):

L = 2 г10Ф cos ( -0 + ф ) + r ² 0 ² + 1 ² ф ² +

■■ ■

+ 2 r1 cos ( -0 + ф ) - 2 r 0 1 sin ( -0 + ф ) +

GMMz r

+

GmMz

r2 - 2r1 sin(ф + П - 0) +12

- 2 c ( 1 - 1 o )².

Составим систему уравнений Лагранжа 2-ого рода описывающих движение КТС с упругим невесомым и тонким тросом:

(M + m)(r - r02) + m(1 - 1ф2) cos(y) + +m (21ф + фф) sin( y ) =

MM ^^^^^^^                                                                                                                                                              ^^^^^^^

r2 д/ r2 + 2 r1 cos( y ) + 12

Mm (r + 1 cos( y ))

3,

(r2 + 2 r1 cos( y ) + 12)2

(1ф2 - 1)mr sin(y) + (21

_     цшг] sin(2)

=

( r ² + 2 r1 cos( Y ) + 1 ²)²

m1 (( r - r0 ²)sin( Y ) + (20т- + 0r )cos( Y ) + 1ф +

Mmr/ ^siⁿ⁽ Y )

+21ф)

( r ² + 2 r1 cos( Y ) + 1 ²)²

- m(0r + 20r-) sin( Y ) + m ( r - r0 ²) cos( Y ) +

Mm ( r cos( y ) + 1 )

(r2 + 2 r1 cos(Y) + 12)2

^-c(1 -10)-

Полученная система является частным случаем системы приведенной в [4]

Рассмотрим частный случай, когда спутник движется по круговой орбите ( r = const ), тогда уравнения (5) существенно упрощаются. Угол 0 изменяется по закону 0 = rot , где го = V 0^Г' и движение КТС описывается уравнениями:

-mrro2I sin(rot - ф) + ml(1ф + 21ф) =

_       ^mrl sm( rot - ф)

=                p

(r2 - 2rl cos(rot - ф) +I2)2

m(rro2 cos(rot - ф) +I - 1ф ) =

цт ( r cos( rot - ф ) - I )

~ ⁺ C ⁽ I ^- I 0 ).

(r2 - 2r1 cos(rot - ф) +I2)2

ОПРЕДЕЛЕНИЕ НАЧАЛЬНЫХ УСЛОВИЙ

До момента стыковки КТС совершает стационарное движение. Считая скорости постоянными из (6) получим уравнение, позволяющее определить длину троса 1 * , соответствующую стационарному движению

т ro 2( r - L )^my + C (I» -l0) = 0, (7) (r -1*)2

где т 1 - масса стыковочного модуля. Будем считать, что стыковка происходит мгновенно и представляет собой абсолютно неупругий удар. Скорости КА и стыковочного модуля до и после стыковки связаны соотношением

• V0(т -m1) + m1ro(r -I) = mVKA,    (8)

где V₀ - скорость выводимого КА (рис. 2а).

После стыковки (рис. 2б) КТС имеет следующие начальные условия _&

фо = 0 , фо = Vs /1*, 1о =1*, 1о = V •      (9)

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ОПЕРАЦИИ ВЫВОДА ГРУЗА

Исследуем влияние на начальной скорости КА на возможность вывода КА на более высокую орбиту. Рассмотрим КТС, состоящую из несущего спутника массой M = 6000 кг , стыковочного модуля вместе с выводимым КА общей массой т = 700 кг и троса изготовленного из материала Dyneema длиной 1 ₀ = 31000 м , модулем Юнга E = 172 ГПа , пределом прочности на разрыв а = 3 ГПа и диаметром d = 1 мм [5]. Вся система двигается по круговой орбите радиусом r = 65 50-10³ м . Из уравнения (7) вычислим длину троса в момент стыковки, если масса стыковочного модуля т 1 =150 кг , получаем 1 * = 31004.57 м .

Используя систему уравнений (6) проведем серию численных расчетов с начальными условиями (9), изменяя начальные скорости V_ф е [-310,310] , V е [-300,300] . Порезульта-там составим диаграмму (рис. 3), на которой отметим точки, соответствующие успешному выводу. Под успешным выводом будем понимать ситуацию, когда в процессе движения КТС ее фазовая траектория попадает в область, определяемую условиями

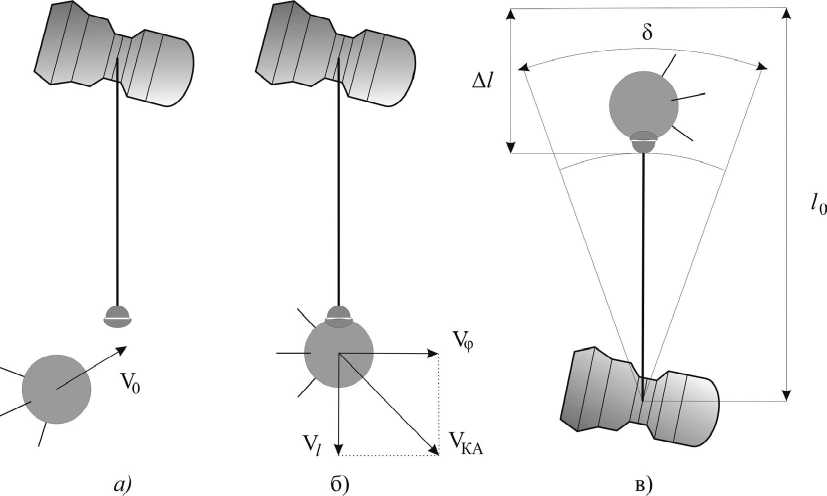
Рис. 2. Стыковка выводимого груза с модулем

Y e [ n - 5 , n + 5 ] , 1 >  1 ₀ -A 1 . (10) где δ и Δ l – параметры, определяющие требуемую область пространства (Рис. 2в) и в момент расстыковки скорость выводимого груза больше или равна круговой

V КА ^≥

GMz r

Приведенная на рис. 3 диаграмма построена для 5 = 3° и A 1 = 100 м .

Белым цветом показаны начальные условия стыковки, при которых условия вывода (10) и (11) не выполняются. Серым точкам соответствуют случаи, когда КТС после стыковки переходит во вращение, что позволяет выводить какой-либо груз на более высокую орбиту. Правая часть диаграммы соответствует начальным условиям, при которых направления угловых скоростей обращения по орбите и закрутки совпадают. В этом случае в наивысшей точке скорости складываются и происходит разгон груза. В левой части наоборот – происходит торможение.

При стыковке с большими скоростями сила натяжения может превысить критическое значение, что приведет к обрыву троса. На рис. 4 показана диаграмма разрыва троса. Области закрашенной белым цветом соответствуют начальные условия, при которых сила натяжения троса во время операции вывода не превышает критического значения Тк,р = ^S . Черными точками показана зона соответствующая разрыву троса.

Таким образом, начальные условия одновременно соответствующие черным (рис. 3) и белым точкам (рис. 4) на соответствующих диаграммах являются точками успешного вывода космического аппарата на более высокую орбиту.

В качестве примера приведем график y ( t ) для некоторых точек (рис. 5).

ЗАКЛЮЧЕНИЕ

В статье рассмотрена операция вывода с помощью переводимой во вращение радиально-ориентированной КТС. Получена математическая модель, описывающая движение КТС. Построена диаграмма начальных скоростей стыковки, которая позволяет судить о возможности вывода КА на более высокую орбиту. А также диаграмма разрыва троса. Полученные диаграммы позволяют осуществить выбор условий стыковки обеспечивающие выведение КА на более высокую орбиту.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект №12-01-31114 мол_а).

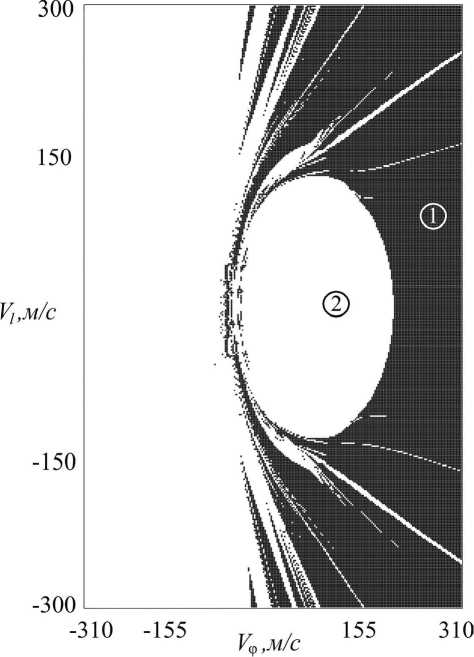
Рис. 3. Диаграмма движения стыковочного модуля

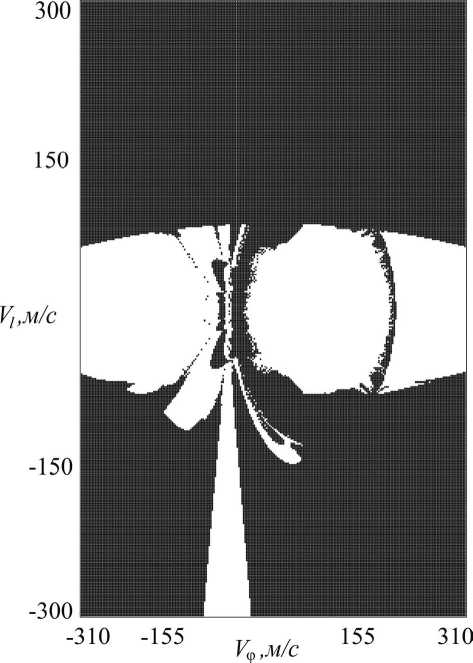
Рис. 4. Диаграмма разрыва троса

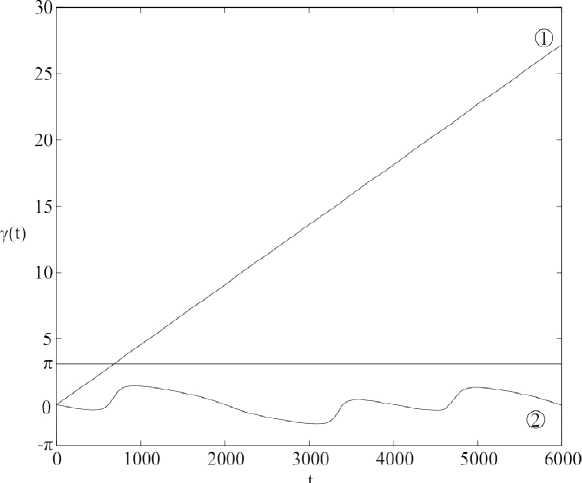
Рис. 5. Графики y ( t ) в двух точках