Использование квадратичной интерполяции для ускорения сходимости непрерывного аналога метода Ньютона
Автор: Никонов Эдуард Германович, Казаков Дмитрий Сергеевич
Журнал: Сетевое научное издание «Системный анализ в науке и образовании» @journal-sanse
Статья в выпуске: 3, 2019 года.
Бесплатный доступ
В работе проанализировано изменение характеристик сходимости Непрерывного аналога метода Ньютона (НАМН) при различном поведении невязки функции в процессе применения метода для решения нелинейного уравнения. Исследовано влияние итерационного параметра в НАМН на область и скорость сходимости. На основе проведённого анализа было предложено ввести дополнительные условия применения ряда модификаций алгоритма НАМН в соответствии с поведением невязки. Предложен подход к оптимизации процесса сходимости НАМН, основанный на применении квадратичной интерполяции приближенных решений, полученных на предыдущих итерациях. Был разработан механизм управления характеристиками сходимости НАМН с использованием ряда управляющих параметров, таких как, коэффициент изменения шага разностной схемы для численного решения дифференциального уравнения НАМН. На основе разработанного механизма управления процессом сходимости предложена модификация непрерывного аналога метода Ньютона.
Итерационные методы, скорость сходимости, нелинейные уравнения, непрерывный аналог метода ньютона
Короткий адрес: https://sciup.org/14122701
IDR: 14122701
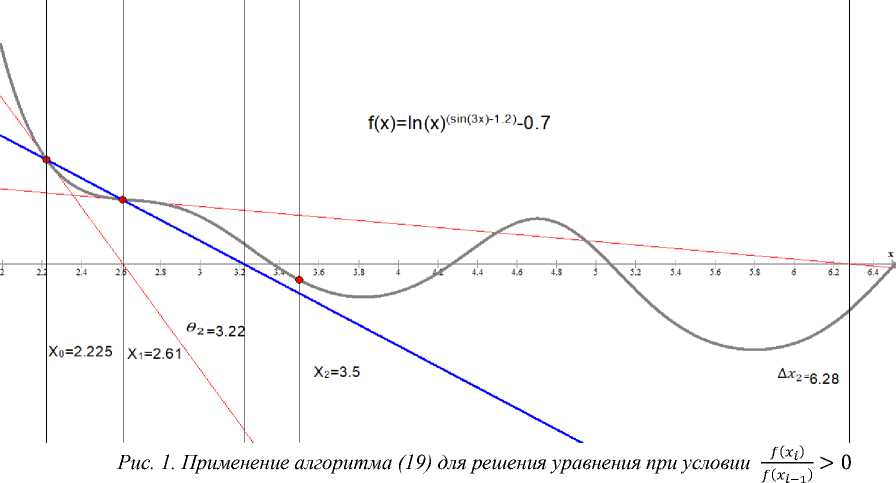
Список литературы Использование квадратичной интерполяции для ускорения сходимости непрерывного аналога метода Ньютона
- Nikonov E.G. One class of conservative difference schemes for solving molecular dynamics equations of motion. arXiv:1605.05714v1 [math.NA].
- Бахвалов Н. С., Жидков Н. П., Кобельков Г. Г. Численные методы. 8-е издание (электронное. - БИНОМ. Лаборатория знаний, 2015.
- Пирумов У. Г. Численные методы: учебное пособие для вузов по направлению "Прикладная математика" / У. Г. Пирумов. - 3-е изд., испр. - М.: Дрофа, 2004.
- EDN: QJNKFV
- Гавурин М. К. Нелинейные функциональные уравнения и непрерывные аналоги итеративных методов [Текст]: Изв. Вузов\\Гавурин М. К. - Матем., №5. - C. 18-31 (1958).
- Жанлав Т., Пузынин И. В. О сходимости итераций на основе непрерывного аналога метода Ньютона // Вычисл. матем. и матем. физ. - 1992. - Том 32. - № 6. - С. 846-856.
- EDN: ZYVLMB
