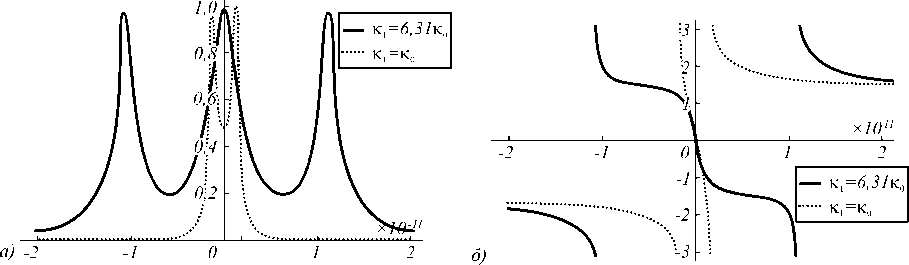Использование массива фотонно-кристаллических резонаторов для интегрирования оптических сигналов во времени

Рост объёма информации в мире и необходимость обрабатывать эту информацию в реальном времени порождают новые требования к вычислительной технике. Значение максимальной рабочей частоты современных электронных вычислительных компонентов достигло естественного предела. Переход на полностью оптические интегрированные на кристалле вычислительные компоненты позволит увеличить скорость обработки информации на несколько порядков и обрабатывать не только действительные, но и комплексные величины [1 – 3]. В связи с этим актуальна оптическая реализация базовых вычислительных операций. Например, в последнее время были предложены оптические интеграторы на основе решёток Брэгга [4] и кольцевого резонатора [5]. Такие интеграторы могут использоваться как в цифровой, так и в аналоговой обработке сигналов.

Среди приложений цифровой обработки сигналов можно выделить использование оптических интеграторов в качестве счётчиков импульсов и элементов сверхбыстрой памяти [6]. Приложения аналоговой оптической обработки сигналов включают решение дифференциальных уравнений различных порядков [7]. Эти приложения особенно актуальны при создании блоков управления автономными мобильными роботами и беспилотными летательными аппаратами. Полностью оптическая реализация такого блока управления на кристалле обеспечит быстродействие, компактность и энергоэффективность устройства.

Размеры предложенных до сих пор интегрированных на кристалле интеграторов на основе решёток Брэгга составляют несколько миллиметров. Интеграторы на основе кольцевых резонаторов более компактны, их размеры составляют десятки микрометров по обоим направлениям плоскости кристалла.

В данной работе предлагаются и численно исследуются наиболее компактные на сегодня оптические интеграторы различных порядков на основе фотонно- кристаллических резонаторов (ФК) [8, 9]. В дальнейшем под интегратором n-го порядка понимается массив ФК-резонаторов, огибающая оптического сигнала на выходе из которого соответствует n-кратному интегрированию огибающей входного сигнала.

Постановка задачи

На рис. 1 показана схема оптического волновода из массива связанных резонаторов. Здесь переменная a i , i = [1, N ] обозначает комплексную амплитуду резонансной моды в i -м резонаторе, к _—1 и К , i = [1, N ] — коэффициенты связности i -го резонатора с массивом, r i = [1, N ] – коэффициенты энергетических потерь i -го резонатора в пространство, p in , p rf , p tr – амплитуды входного, отражённого и прошедшего полей соответственно.

1"1       1'2           rN_! rN

Рис. 1. Схема оптического волновода из массива связанных резонаторов

Рассмотрим вариант, при котором резонаторы в массиве настроены на одну резонансную частоту. Тогда, согласно временной теории связанных мод [10], амплитуды электромагнитного поля в каждом из резонаторов связаны уравнением, которое в матричном

виде записывается следующим образом:
Ma = P in ,	(1)
' 5 1 + K 0   i K i    0    L     0        0    л i K 1      5 2    i K 2   • •      о         0 0     i K,    53   •    0       0 m =      .        .2     3. :     :     mo i K n -2     0 0      0    0    •    5N -1     i K N -1 .   0     0    0    • i K N -1   5n +K n ;	, (2)
где 5 j = i ( ®-® 0) + r j = 5 + r j - переменная, учиты-

вающая рассогласование относительно частоты резо- нансной моды и энергетические потери резонатора в пространство, i - мнимая единица, a =[a1 a2 ••• aN ] T ,

P in = [ - i Ж Pn 0 l 0] ^T .

Функцию пропускания такой системы можно записать в виде [11]

T ( 5 ) = pr-p _n

² ( ^{- i} ) N ^- 1 V^K0 ^K N ^K 1 ^K 2 ^{L K} N -1 det( M )

На рис. 2 показан результат интегрирования огибающей оптического импульса длительностью 100 пс резонаторами с добротностью 10⁵ и 5×10⁵. Добротность резонатора Q связана с κ 0 соотношением Q = to ₀ / (4 к ₀). Из рисунка видно, что чем выше добротность резонатора, тем медленнее затухает огибающая интегрированного сигнала.

где

P tr = ^{- i}V²^ a N = ²V^K 0 ^K N [ ^М ] _N ,1 P in ,

det( M ) – определитель матрицы M .

Для одного резонатора выражение (3) преобразуется в вид

T ( 5 ) =

2 K

5 + 2k₀

Здесь и далее для простоты мы пренебрегаем потерями резонатора в пространство.

Интегратор 1-го порядка

Рассмотрим, каким образом выражение (4) аппроксимирует интегратор 1-го порядка. Поляризованное электрическое поле с огибающей P in ( t ) запи-

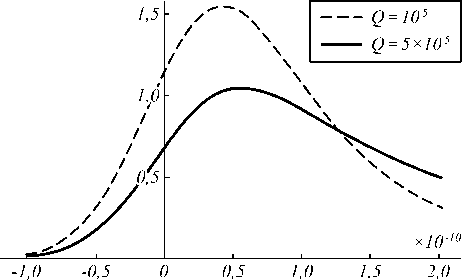
Рис. 2. Результат интегрирования 1-го порядка огибающей

оптического импульса длительностью 100 пс резонаторами с добротностью 105 и 5×105

Покажем, что использование вместо одного резонатора массива из нескольких резонаторов позволяет выполнять интегрирование высоких порядков. Для двух резонаторов выражение (3) можно записать в виде

сывается в виде

E ( x , t ) = P in ( t - x^v g ) exp ( i m ₀ x - i to ₀ 1 ) =

T 2 ( 5 ) =   i ² ^^

( 5 + К) ) +К 1

.

M

= J R ( to-to ₀ ) exp ( i m ( to ) x - i to t ) d to ,

-M

где R ( to ) - спектр огибающей сигнала, m ( to ) - волновое число ( m ₀ = m ( to ₀)), v g - групповая скорость.

На выходе линейной системы, описываемой комплексной функцией пропускания H ( to ), огибающая входного импульса (5) преобразуется в

M

P r ( t ) = J R ( to ) H ( to ) exp ( i to t ) d to =

-M

= Pin (t )* h (t) , где символ * обозначает операцию свёртки и h(t) – спектр комплексной функции пропускания H (to) .

Импульсный отклик линейной системы с передаточной функцией (ПФ) вида (4) равен hl ( t ) = -K0exP (-K0t ) u (t),                          (7)

где u ( t ) – функция Хэвисайда.

Подставляя соотношение (7) в (6), получим выражение для огибающей выходного импульса

t

P ( t ) = -K 0 J P in ( T ) exp ( - i K 0 ( t - T ) ) d T .         (8)

-M

Правая часть данного уравнения выражает интеграл огибающей входного импульса с экспоненциальным весом.

Для массива из трёх резонаторов функция пропускания записывается в виде

T 3 ( 5 ) =

___________ ^2к 0 ^К 1 ^К 2 ___________

5 ( 5 + К 0 ) ² + ( 5 + К 0 ) ( к 2 + к 2 )

Подставляя выражения (9) и (10) в соотношение (6) в качестве комплексной функции пропускания, получим огибающую выходного сигнала для линейной системы из двух и трёх резонаторов соответственно.

Например, импульсный отклик линейной системы с ПФ вида (9) равен h2 (t) = k0L-(k° +iK1)t (L2iK1 t -1)u(t).(11)

Можно получить соотношение h2 (t) = 2iK0K11 exp (-k0t) u(t).(12)

Подставляя соотношение (12) в (6), получим выражение для огибающей выходного импульса интегратора 2-го порядка:

tT

Ptr (t) = iK0K1 J J Pin (T1)L-iK0(t-T1) dT1dT2.(13)

T 2 =-M T 1 = -M

В работе [12] приведены обобщающие формулы для интеграторов более высоких порядков на основе решёток Брэгга.

ПФ идеального интегратора огибающей оптического сигнала с несущей частотой to o записывается в виде

H int ( 5 ) = - 1/ 5 .                                      (14)

Наибольшие отличия между функциями (4) и (14) наблюдаются в окрестности to 0 . Это приводит к тому, что интегрирование импульсов с узким спектральным диапазоном приводит к большим погрешностям. При этом чем меньше добротность резонатора, тем значительнее отличие (4) от (14) в окрестности to o и тем выше ошибка интегрирования.

На рис. 3 показан результат интегрирования резонаторами с добротностью 105 и 5×105. На вход подаётся оптический сигнал с огибающей, соответствующей первой производной Гауссова импульса длительностью 100 пс. Примеры входных сигналов показаны на рис. 4.

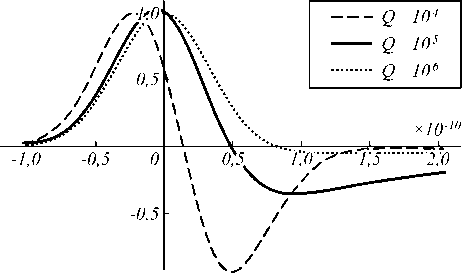
Рис. 3. Результат интегрирования резонаторами с добротностью 104, 105 и 106. На вход подаётся оптический сигнал с огибающей, соответствующей первой производной Гауссова импульса длительностью 100 пс

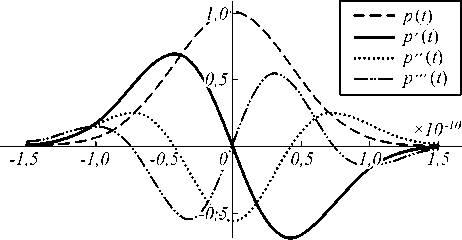
Рис. 4. Исходный Гауссов импульс длительностью 1 пс и три его первые производные

В работе [13] описано использование ФК-резонатора в качестве оптического дифференциатора. Функция комплексного отражения такого резонатора записывается в виде

H df ( ⁵ ) =

s

^{5 + К} 0

Выражение (15) отличается от функции идеального дифференциатора ( H_id f ( 5 ) = - 5 ) в окрестности to o количественно, но не качественно. Поэтому дифференцирование сигналов с узким спектральным диапазоном высокодобротным резонатором не приводит к погрешностям, аналогичным тем, которые показаны на рис. 3.

Причины отличия (4) от (14) вне окрестности too различны для разных типов резонаторов. Например, для кольцевого резонатора погрешность интегратора на высоких частотах определяется величиной FSR (free spectral range) и зависит, в частности, от радиуса резонатора. Для ФК-резонаторов погрешность интегратора на высоких частотах определяется влиянием соседних резонансных мод и шириной запрещённой зоны фотонного кристалла.

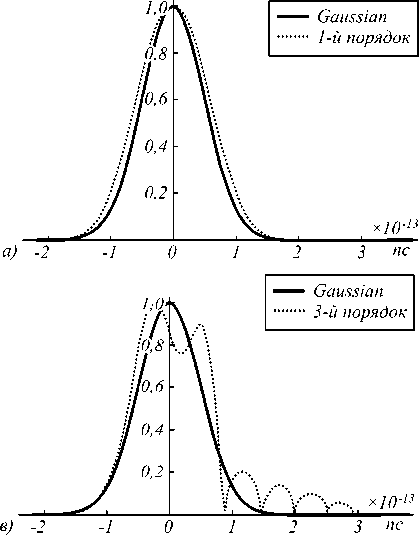
На рис. 4 показаны входные тестовые импульсы. Это исходный Гауссов импульс длительностью 1 пс и три его первые производные. Таким образом, интегратор должен восстановить Гауссов импульс из его первой производной. Интеграторы 2-го и 3-го порядков должны восстановить Гауссов импульс 2-й и 3-й производных соответственно.

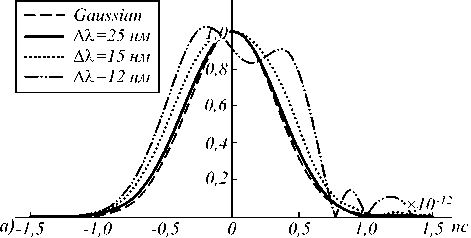
На рис. 5 а показаны результаты интегрирования первой производной Гауссова импульса длительностью 1 пс для различных значений FSR. Добротность резонатора составляла 5×10⁴. Из рисунка видно, что резонаторы со значениями FSR, равными 12 нм и 15 нм, интегрируют входной сигнал с большими искажениями. Высокое качество интегрирования достигается при значении FSR, равном 25 нм. На рис. 5 б показаны аналогичные результаты интегрирования первой производной Гауссова импульса длительностью 150 фс. Видно, что хорошее качество интегрирования достигается для значения FSR, равного 120 нм. Создание кольцевых резонаторов с таким большим FSR затруднительно. Подходящим кандидатом для интегрирования субпикосекундных импульсов представляются ФК-резонаторы.

---Gaussian

--- NX=120нм

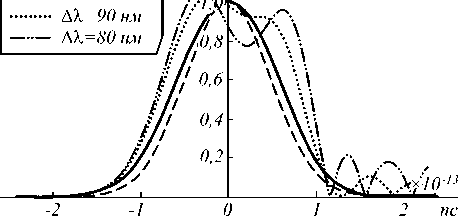
Рис. 5. Результаты интегрирования 1-й производной Гауссова импульса для значений FSR 25 нм, 15 нм и 12 нм для импульса длительностью 1 пс (а) и 120 нм, 90 нм и 80 нм для импульса длительностью 150 фс (б).

Добротность резонатора составляла 5×104

Пример интегратора на основе ФК-волновода

Рассчитаем параметры конкретного ФК-резонатора, выполняющего интегрирование оптического сигнала. В качестве такого резонатора выберем элемент на основе гребенчатого ФК-волновода. По сравнению с двумерными ФК-структурами в слое [8, 9] резона- торы на основе гребенчатого ФК-волновода обладают меньшей площадью и естественным образом интегрируются в волноводную геометрию соединений на кристалле. На рис. 6а показан один из вариантов резонатора на основе гребенчатого ФК. Здесь дефект, в котором возбуждается резонансная мода, формируется уменьшением радиуса отверстий в окрестности дефекта.

b2_ 2a,

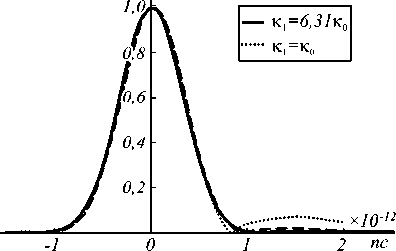
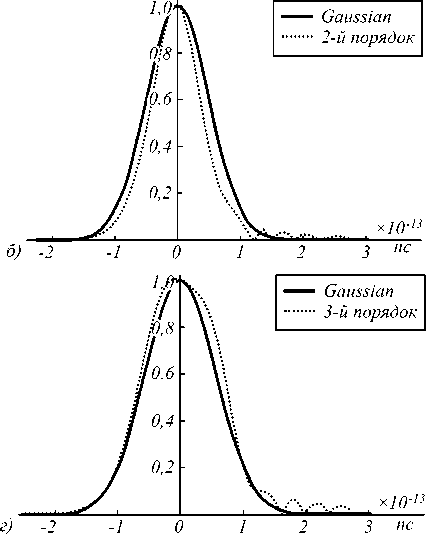
|oooooo

а)

Hie

nreg

ооооооо/

2a2

ft tap Mreg/2

б)

Рис. 6. Схема резонатора на основе ФК-волновода (а), массив из 2 таких резонаторов (б)

Рассмотрим массив ФК-резонаторов, изображённый на рис. 6б. Коэффициент связности резонаторов в массиве определяется nreg – количеством отверстий с одинаковым (максимальным) радиусом между дефектами. Можно показать [14], что для двух соседних резонаторов с добротностями Q1 и Q2 коэффициент связности равен k= to— = -^ a " nreg

4 Q1Q2 4Q0

где Q0 – добротность резонатора, содержащего только отверстия зоны дефекта, too - резонансная частота, соответствующая длине волны Брэгга, κg и Λ – сила решётки (grating strength) и период решётки Брэгга соответственно. Величина a может быть аппроксимирована с помощью расчёта добротности резонатора для различных значений n_reg.

Для расчёта характеристик резонатора использовался трёхмерный параллельный метод FDTD [15]. На рис. 6а введены обозначения геометрических параметров одного резонатора из массива. Волновод имеет ширину w = 490 нм и высоту h = 220 нм, состоит из кремния (n = 3,46) и окружён воздухом. Отверстия в регулярной части волновода заполнены воздухом, имеют радиус R = 100 нм и отстоят друг от друга на a = 330 нм. В табл. 1 содержатся значения радиусов отверстий и периода решётки в зоне дефекта (n_reg=12). Эти геометрические параметры обеспечивают возникновение энергетической запрещённой зоны (bandgap) для TE-поляризации в волноводе [14]. Левая и правая границы запрещённой зоны равны 1,46 мкм и 1,67 мкм соответственно. Размер запрещённой зоны – 210 нм. Длина волны резонансной моды 1,57 мкм находится в центре этой зоны.

Таблица. 1. Геометрические параметры ФК-резонатора на рис. 6a

a1	b1	a2	b2	a3	b3	a4	b4	a5	b5	a6	b6
40	255	55	350	65	365	75	375	85	385	95	395

Если количество отверстий с одинаковым радиусом слева и справа равно n_reg/2, как показано на рис. 6б, то выполняется следующее условие

K =кN = Kj, j = 1,N-1.

Рассчитанный резонатор способен качественно интегрировать субпикосекундные импульсы. На рис. 7а показан результат интегрирования первой производной Гауссова импульса длительностью 150 фс. Добротность резонатора составляла 5×10⁴. Результаты интегрирования 2-й и 3-й производных импульса такой же длительности интеграторами 2го и 3-го порядков соответственно показаны на рис. 7б, в. Интегратор 2-го порядка состоит из двух резонаторов, показанных на рис. 7б. Интегратор 3-го порядка содержит три таких резонатора. Коэффициенты связности для резонаторов в каждом из интеграторов задаются соотношением (17). Рис. 7б, в демонстрируют, что качество интегрирования ухудшается с ростом порядка интегрирования для импульсов одинаковой длительности. На рис. 7г показан результат интегрирования 3-го порядка импульса длительностью 200 фс.

Размеры интегратора первого порядка на основе ФК-резонатора на рис. 6а составляют 6,0×0,5×0,2 мкм для длины волны 1,57 мкм. Интеграторы 2-го и 3-го порядков имеют размеры 12×0,5×0,2 мкм и 18×0,5×0,2 мкм. Таким образом, данный интегратор является в десятки раз более компактным, чем любой из представленных ранее.

До этого в данной статье полагалось, что коэффициенты связности в массиве резонаторов задаются соотношением (17). В соответствии с формулами (4), (9) и (10) чем меньше величины κ_i, тем ближе соответствующие ПФ к ПФ идеального интегратора. При этом величины κ₀ и κ_N определяются параметрами самого резонатора, а величины кj, j = 1, N -1 могут быть подобраны путём изменения расстояния между резонаторами в массиве. Например, уменьшая количество отверстий между дефектами в ФК-волноводе, мы можем увеличить коэффициенты связности. В работе [16] описана аналогичная процедура для интеграторов на основе решёток Брэгга.

Величины коэффициентов связности влияют также на количество энергии на выходе интегратора. Увеличивая κ_i, можно повысить энергетическую эффективность интегратора. Тем не менее, это приводит к дополнительным искажениям ПФ. На рис. 8а показаны значения амплитуды ПФ массива из трёх резонаторов для двух вариантов коэффициентов связности. Во-первых, для варианта, описываемого соотношением (17), и, во-вторых, для соотношения 6,31 к₀= 6,31 к_N = кj, j = 1,N-1. Здесь значение 6,31 соответствует a³= 1,8483. Таким образом, мы увеличиваем коэффициенты связности, оставляя между дефектами только отверстия с переменным радиусом и убрав 3 отверстия с постоянным радиусом. На рис. 7б показаны соответствующие значения фазы ПФ. Добротность резонатора составляла 10⁵.

Из рис. 8б видно, что повышение коэффициентов связности резонаторов приводит к расширению зоны дополнительного фазового скачка передаточной функции в центре.

Рис. 9. Результаты интегрирования 3-го порядка для различных значений коэффициентов связности резонаторов

Рис. 7. Результаты интегрирования соответствующих производных Гауссова импульса длительностью 150 фс ФК-резонатором с добротностью 5×104 (а), массивом из двух ФК-резонаторов (б), массивом из трёх ФК-резонаторов (в) и результат интегрирования 3-й производной Гауссова импульса длительностью 200 фс массивом из трёх ФК-резонаторов (г)

Рис. 8. ПФ массива из трёх резонаторов для двух вариантов коэффициентов связности: амплитуда ПФ (а), фаза ПФ (б)

На рис. 9 показаны результаты интегрирования 3й производной Гауссова импульса длительностью 10 пс массивами резонаторов с передаточными функциями, представленными на рис. 8. Дополнительный фазовый скачок передаточной функции в центре влечёт ухудшение точности интегрирования.

Заключение

В работе предложен и рассчитан компактный интегратор комплексной огибающей оптического сигнала на основе фотонно-кристаллического волновода. Данный интегратор является в десятки раз более компактным, чем любой из представленных ранее. Размеры интегратора линейно зависят от порядка интегрирования. Показано, что предложенный интегратор может иметь размер свободной спектральной зоны более 200 нм. Это позволяет с высокой точностью интегрировать оптические импульсы субпикосекундной длительности.

Работа выполнена при поддержке грантов РФФИ №№ 13-07-97002, 13-07-13166, 14-07-97008, 14-0797009 и Программы № 5 фундаментальных исследований ОНИТ РАН «Фундаментальные проблемы физики и технологии эпитаксиальных наноструктур и приборов на их основе», Министерства образования и науки РФ.