Использование математических методов для оптимизации взаимосвязей между элементами имущественных комплексов

Правомерен вопрос: а может ли расположение развилок вне связываемых объектов уменьшить общую длину пути, соединяющего эти объекты? Для случая, когда четыре объекта расположены в углах квадрата со стороной равной 1 (условной единице), кратчайший путь, соединяющий объекты с разветвлением только в объектах, имеет длину ( l ) равную 3, тогда как расположение разветвления в пересечении диагоналей квадрата дает l » 2,828 (короче более чем на 5,7 %), а при Н-образной конфигурации соединения объектов (развилки в точках F₁ и F₂ , из которых смежные стороны видны под одним и тем же углом - 120°) « 2,732 (еще короче на 3,4 %). Ответ в иллюстрациях приведен на рисунке 1.

Рис. 1. Варианты оптимальной длины коммуникаций в зависимости от выбора мест разветвлений: а) разветвления на территории связываемых объектов ( l = 3); б) развилка на пересечении диагоналей квадрата ( l = 2,828); в) разветвления в точках F₁ и F₂ , из которых смежные линии видны под одним и тем же углом – 120° ( l = 2,732)

Итак, улучшение результата возможно, а поиск оптимальных схем соединения объектов зависит от количества объектов, их взаимного расположения и мест развилок.

На побережье Северного ледовитого океана (район Крайнего Севера) отработаны четыре шахты горно-обогатительного комбината, основания вертикальных стволов которых имеют одинаковую отметку - ниже уровня моря со взаимным расположением, показанным на рисунке 2.

Совет директоров горно-обогатительного комбината по согласованию с местными природоохранными органами принял решение об использовании отработанных шахт A , B , C и D для хранения дизельного топлива в ледяной «колбе».

у км, .

С(11, 27) 0

27-

В (4,10)

3,96--                                              ©

2--         /4(10,2)0                              0(28,28; 3,96)

"01       4          101*1                   21           28,28 кмХ

Рис. 2. Расположение оснований вертикальных стволов шахт – A , B , C , D (ось 0x проходит вдоль побережья океана)

Задача 2.

Составить оптимальную схему проходки горизонтальных ледяных тоннелей, соединяющих основания вертикальных стволов шахт – A (10, 2), B (4, 10), C (11, 27) и D (28,28; 3,96). Найти общую протяженность ( L ) ледяных тоннелей и вычислить минимальные совокупные затраты ( Z _min) реализации проекта, если усредненная стоимость проходки 1 километра ледяного тоннеля (горизонтальной ледяной выработки) равна S тысяч рублей.

Замечание . Евклидова задача Штейнера имеет алгоритмы для решения прикладных задач при небольшом количестве объектов (порядка 10). Общего алгоритма не существует, что связано с потерей дискретности. Исходные данные постановочной задачи № 2 относятся к случаю, когда составление оптимальной схемы имеет точное и эффективное решение (ресурсозатратные технологии заменяются на ресурсосберегающие) через построение точек Штейнера. Важнейшие свойства точек Штейнера, которые востребованы для решения рассматриваемой задачи:

• •    точка Штейнера имеет степень d = 3 (т. е. она является развилкой для трех направлений);

• •    для любого объекта [в нашем случае A (10, 2), B (4, 10), C (11,27) и D (28,28; 3,96)], из множества связываемых схемой, выполняется условие: степень d <  3; если d = 3, то

угол между любыми двумя смежными направлениями (линиями) должен быть равен 120°; если d = 2, то этот угол должен быть больше или равен 120°;

• •    если в исследуемой схеме N объектов, то количество точек Штейнера (n) будет в пределах 0 <  n <  N - 2 (для задачи 2: 0 <  n <  2).

Решение . Количество и построение точек Штейнера зависит от свойств исходного четырехугольника ABCD . Для определения формы четырехугольника ABCD (прямоугольник или квадрат, параллелограмм или ромб, трапеция: простая или равнобедренная, простой четырехугольник):

• а)    вычислим длину каждой из сторон – AB , BC , CD и AD ,

• б)    установим взаимное расположение сторон на предмет их параллельности и (или) перпендикулярности.

AB = 7 (4 - 10)² + (10 - 2)² = V36 + 64 = ^00 = 10;

BC = 7(11 - 4)² + (27 - 10)² = /338 « 7324 х 1 1 +

2 х 324

« 18 х ( 1 + 0,022 ) « 18,4² ;

CD = 7(28,28 - 11)² + (3,96 - 27)² = 7 829,44 = 7784 х | 1 + ^45,44 | « 28 х ( 1 + 0,29 ) « 28,8 ; (     2 х 784 J ^{v 7}

AD = 7(28,28 - 10)² + (3,96 - 2)² = 7338" = 7324" х | 1 +

2 х 324

« 18 х ( 1 + 0,022 ) « 18,4.

Следствие 1. Четырехугольник ABCD не является ни квадратом, ни ромбом, т. к. AB # BC # CD # AD .

У - У -i   х - Х                      — — —

Используя формулу ----- =---- — , составим уравнения прямых AB , BC , CD и

У 2 ^- У 1    ^Х 2 ^{- Х} 1

AD , на которых лежат стороны четырехугольника ABCD (AB с AB , BC с BC, CD с CD и AD с AD ), а для каждого уравнения прямой ax + by + c —0 по формуле k = -b вычислим угловые коэффициенты kAB, kBC, kCD и kAD , по которым определим взаимное расположение сторон AB, BC, CD и AD.

² Используя понятие дифференциала, можно «вручную» вычислить корень любой n-й степени: если

1    f1 -1]    Пх f (X) = nx , то f'(X) =-х X1 n J =----- т. к. f (х + Дх )= f (х )+ f'(х )хДх , то n          n х х , пх + Дх = п/х + -^Х- х Дх = л/х х f 1+ ^^] .

n х Х

n х Х

Например, 6 67,84 = 6 64 х 1 1 + ^4- |« 2 х ( 1 + 0,01 ) « 2,02.

6 х 64

AB ° y- ² = ~8x+6y—⁹²=°; k A® =- 8 ~ k A ”-1,3... ;                                                     6;

BC ^ ^У -1° = — ~ 17x - 7y + 2 = °; k = ¹⁷ ~ k ” 2,4 17      7 ;                          ^BC 7 ; ^BC

CD

y - 27

- 23,04

^ -11 ~ 23,°4x + 17,28y - 72° = °; k ^ =- 23^4 ~ k ^ «- 1,3...

17,28 ;                                   ^CD 17,28 ; ^CD

AD « У- ² =

1,96   18,28

~ ;

1 96

1,96x - 18,28y + 16,96 = °; k— = -¹96- ^AD 18,28 ;

~

^k AD « °,1 .

Следствие 2. Прямые AB и CD параллельны, т. к. k AB = k CD «- 1,3..., отсюда AB II CD ,

• т. к. AB с AB , а CD с CD .

Вывод 1 . Четырехугольник ABCD – равнобедренная трапеция ( AB || CD , BC = AD « 18,4 ).

Алгоритм размещения двух точек Штейнера для равнобедренной трапеции ABCD (рис. 3): на перпендикуляре P₁P₂ , проведенном через середины оснований трапеции ( AB и CD ), отметим две точки F₁ и F₂ , отвечающие свойству точек Штейнера, а именно Z AF 1 B = 12°°, Z CF 2 D = 12°°.

Из условий задачи и алгоритма выбора точек F₁ и F₂ следует:

L = AF 1 + F 1 B + F 1 F₂ + F ₂ C + F ₂ D ;                                                    (1)

A AF 1 B и A CF 2 D - равнобедренные,

т. к. A P F 1 A = A PFB

как прямоугольные с общей высотой ( P 1 F 1 и P 2 F 2 )

A P₂F ₂ C = A P₂F₂D J и равными основаниями;

Z P 1 AF 1 = Z P 1 BF 1 = Z P ₂ CF ₂ = Z P ₂ DF ₂ = (j8Q ⁰ - 12° ⁰ )^2 = 3° ⁰ .

Из свойств (2) и (3) следует:

AF 1 = F 1 B = 2 P 1 F 1 ;

CF 2 = F 2 D = 2 P ₂ F 2

(катет лежащий против угла в 30° равен половине гипотенузы).

Поскольку F 1 F ₂ с P 1 P ₂, т. е. лежат на одной прямой

F 1 F 2 = P 1 P 2 - P 1 F 1 - F 2 P 2 .

Подставляя (4), (5) и (6) в (1), получим

L = P 1 P ₂ + 3 x ( P 1 F 1 + P ₂ F ₂ ) .

Из A F 1 P 1 A и A F ₂ P ₂ C находим P 1 F 1 и P ₂ F ₂ соответственно:

P 1 F 1 = P 1 A x tg 3° ⁰ =

AB 1 AB x Va ^x 73 =

PF = P₂C x tg 3°^o = CD x -D = ^{CD x} ^3

22   2           2    3     6

P F i + P 2 F 2

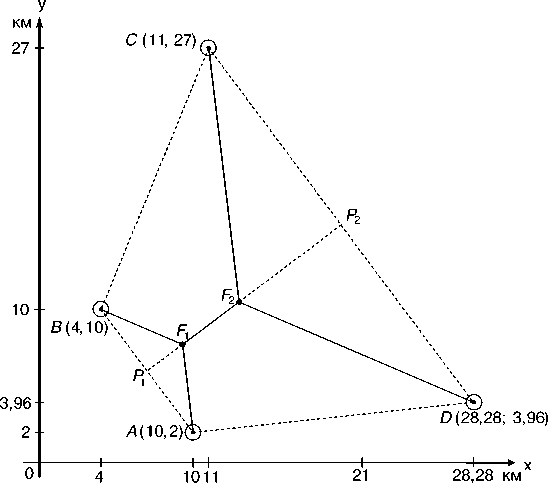
Рис. 3. Построение точек Штейнера F₁ и F₂ для равнобедренной трапеции ABCD

_---X

( AB + CD ) .

Поскольку AB || CD (см. следствие 2), P1P2 вычислим3 как расстояние от произвольной точки прямой CD , например C (11,27), до прямой AB : 8x + 6y – 92 = 0.

P 1 P 2

18 x 11 + 6 x 27 - 92| _ ^8 + 162 - 92| _ ₁₅₈

78 2 + 6 2     "    7w0    "^o"

.

Подставляя (10) и (11) в (7), получим искомый результат:

L = 15,8 + ^3 x ( AB + CD ) re 15,8 + ^3 х

( 10 + 28,8 ) _ 15,8 + 19,4 х 73 re 49,4 км

Z min _ L X S re 49,4 X S тыс . р .

Примечание . Если точку Штейнера выбрать на пересечении диагоналей равнобедренной трапеции ABCD , то результат ( d ) будет хуже на величину а re ( 50 - 49,4 ) км re 0,6 км , т. к.

d _ 2 AC _ 2 X V ( 11 - 10 ) 2 + ( 27 - 2 ) 2 = 2 х 7 1 + 625 _ 2 х 7626 re 2 х 7625 х l 1 +

) 2 X 625 J

_ 2 x 25 x | 1 +       U 50 x ( 1 + 0,0008 ) re 50

I 1250J ^{v 7}      .

Ответ : L re 49,4 км ; Z min re 49,4 х S тыс . р .

³ Используем формулу: h _

I ax 0 + by 0 + c| 7 a ² + b ²

где h – расстояние от точки H ( x ₀, y ₀) до прямой ax + by + c =0.

Резюме . Реализация проекта, сформулированного в задаче 2, позволяет просвещенному собственнику заменить ресурсозатратные технологии на ресурсосберегающие, поднять социальный статус северного региона, усилить конкурентоспособность, опережающими темпами развить геологоразведку, защитить население и территорию от техногенных катастроф и террора, и как следствие – укрепить безопасность и социальную, и экономическую.

Размещение стратегического объекта (хранилище горюче-смазочных материалов – ГСМ) в пространстве вечной мерзлоты и возможность самостоятельного регулирования объемов хранилища освобождают собственника от необходимости ежегодного «северного» завоза ГСМ, что на порядок:

• •    сокращает затраты по перевозке ГСМ по тундре (в ледяную «колбу» ГСМ закачивается сразу с танкера, т. к. вертикальный ствол шахты А находится вблизи причала);

• •    увеличивает срок эксплуатации автотранспорта и гусеничной техники.

Задача 2’ (для самостоятельного решения).

• •    Сформулировать вербальную модель задачи для случая, когда объекты размещены в вершинах прямоугольника со сторонами 8 и 6 км. (ключ: задача 2 и ее решение).

• •    Построить точки Штейнера.

• •    Найти решение по критерию: минимальная суммарная длина прямолинейных соединений вершин прямоугольника.

• •    Составить виртуальную схему соединения вершин прямоугольника через точки Штейнера.

• •    Вычислить минимальные совокупные затраты реализации проекта, если стоимость 1 километра коммуникации составляет S тысяч рублей.

Ответ :    Длина ~ 18,4 км.

Прямые затраты ~ 18,4 S тыс. р.

Вопросы

• 1.    Сколько существует альтернатив для построения точек Штейнера в прямоугольнике?

• 2.    Если точку Штейнера выбрать на пересечении диагоналей прямоугольника, каким будет результат А ?