Использование математического аппарата при решении прикладных задач

В настоящее время математический аппарат считается одним из главных решением для ряда задач в информатике и программировании. В математическом аппарате существует три основные задачи: задача создания алгоритма поиска множества пользователей по заданным параметрам, задача установки сервера необходимой мощности, задача оптимизации сети.

Задача создания алгоритма поиска множества пользователей по заданным параметрам . Для начала необходимо записать постановку задачи с точки зрения математики. Существует комбинация множеств М = {М 1 ,М 2 , ,„,М_П}.        Необходимо        найти        подмножество

5:5 с {М у , М у ₊₁, ..., М_к} VjVk: j < к <п. Комбинация множеств – n -ое количество непустых, взаимно пересекающихся множеств, образующих отдельные подмножества, которые могут быть как пустыми, так и с n -ым количеством элементов.

Стоит отметить, что в зависимости от того в какое количество надмножеств входит искомое подмножество, пересекаются и вычитаются различные множества. Например, в случае, если количество вхождений подмножества численно равно количеству множеств в комбинации, то для нахождения требуется пересечь все подмножества сразу. А в случаях, когда количество вхождений меньше, пересекаются все надмножества искомого подмножества, и вычитаются остальные множества комбинации.

Под вхождением подмножества понимается характеристика подмножества 5, определяемая количеством надмножеств М [ ,в которые входит подмножество 5, из комбинации множеств М.

Введем функцию Ocn(S), Осп от слова «Occurrance» - вхождение. Данная функция определяет все надмножества в которые входит аргумент.

Осп(5) = {Му, Му+1.....М6)

Теперь необходимо понять в какие множества М ^ не входит подмножества 5. Для этого обозначим всю комбинацию М как универсальное множество 1. Тогда:

1\5 = 5

Следовательно, множества, в которые не входит 5 можно записать так: Осп(5) = {М^М^ .....М₅)

Теперь можно вывести формулу нахождения отдельного подмножества 5:

S = (Mj П Mj+1 П ... П Mk) \ (Mk и мк+1 и ... и Mg)

Перепишем формулу в виде:

S = Q Ocn(S) \ [J Ocn(S)

Алгоритм решения задачи поиска множества пользователей по заданным параметрам представлен на рисунке 1.

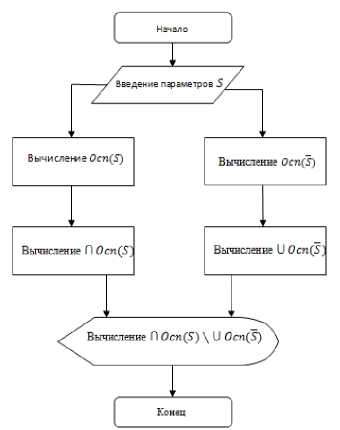
Рисунок 1 - Алгоритм решения задачи

Таким образом, решение первой задачи описано выше. Перейдем к решению второй задачи.

Задача установки сервера необходимой мощности . Предположим, что создана некая организация, нуждающаяся в определенной системе. Она должно выполнять требования:

- вычислительная система должна выдерживать суточную нагрузку;

- затраты на ее обеспечение должны быть минимальными, таким образом мощная система данной организации не нужна.

Вышеописанная организация предоставила график роста количества отправляемых на обработку данных со временем, который предоставлен на рисунке 2.

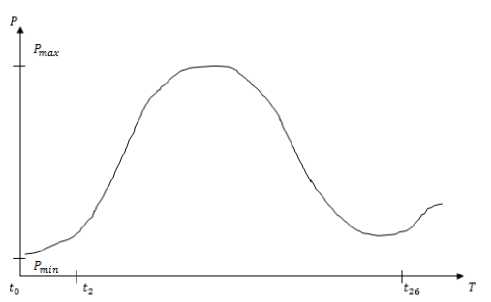
Рисунок 2 - График обработки данных

В данном случае неизвестно, какая функция описывает кривую, поэтому имеет смысл провести аппроксимацию. Приближением (аппроксимацией) функции f(x) называется отыскание функции^ (%) близкой в некоторомсмысле к f(%)[1]. Аппроксимирующей функцией

хорошо подойдет sinx^. ее график схож с данной кривой. Тогда аппроксимирующая функция принимает следующий вид:

f(t) = ct sin(kt + b) + с : E_f ( _t )

Domin ’ ^K max ] ’ ^K min >  ^P min , ^ max >  ^P max

Теперь выразим примерное количество запросов в сутки:

t26                                           t26                         t26

P = I J (c sin(kt + b) + c) dt\ = I — J sin(kt + b~)dt + J cdt\

I t 2                                                           t 2                                    t 2

Отрезок [t2; t26] - 24 часа.

Таким образом, вычислив данный интеграл, возможно, установить систему необходимой мощности. Теперь перейдем к третьей задаче.

Задача оптимизации сети. Существует некоторое количество информационных сервисов, которые отправляют определенные данные на обработку на серверы. Существует несколько видов, различных по мощности, видов серверов. Необходимо реализовать алгоритм определения наименьшего количества серверов для любого количества информационных сервисов. Пусть L = {11,12,... ,ln} - множество серверов с разной вычислительной мощностью, причем, чем больше индекс, тем больше мощность. К = {k1,k2, ^ ,k[} - совокупность произвольных нагрузок различных информационных сервисов, Н = {h1, h2, ..., by}- множество серверов необходимых для функционирования сети. Для функционирования сети должно выполняться условие:

z^^z

к

НЕН    кЕК

То есть совокупная мощность должна быть больше или равна совокупной нагрузке. Для решения данной задачи воспользуемся целочисленным делением и делением по модулю.

Алгоритм выполнения предоставлен на рисунке 3.

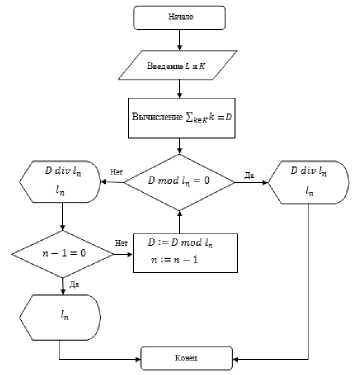
Рисунок 3 - Алгоритм выполнения

Таким образом, решив данные задачи, было показано и доказано, что математический аппарат в настоящее время является мощнейшим инструментом для решения прикладных задач.