Использование математического моделирования для оценки погрешности измерения информативных параметров гармонических сигналов

напряжения и тока одновременно измеренным в произвольный момент времени, причем вторые мгновенные значения сигналов сдвинуты относительно первых на угол Δα, а третьи МЗ напряжения и тока сдвинуты относительно вторых также на угол Δα. Однако реализация метода предусматривает использование четырех ФБ и шести аналого-цифровых преобразователей. Кроме того, применение метода предусматривает анализ МЗ напряжений и токов на ноль и измерение дополнительных мгновенных значений сигналов, если хотя бы одно из значений равно нулю. В нашей статье производится анализ нового метода [7], реализация которого снижает аппаратурные затраты и сокращает время измерения.

Метод измерения параметров с пространственным разделением мгновенных значений сигналов. Метод заключается в том, что формируют два дополнительных напряжения, которые сдвинуты относительно входного на углы Δα и 2Δα и дополнительный ток, сдвинутый относительно входного на угол Δα. В момент, когда дополнительное напряжение, сдвинутое относительно входного на угол 2Δα переходит через ноль, одновременно измеряют МЗ входных и дополнительных сигналов напряжения и тока. Параметры ГС определяют по измеренным значениям. Временные диаграммы, которые поясняют метод, приведены на рис. 1.

Если входные напряжение и ток имеют гармонические модели u 1 ( t ) = U m sin m t и i 1 ( t ) = I m sin ( m t + ф ) , то дополнительные сигналы принимают следующий вид: U 2 ( t ) = U m sin ( m t + Aa ) , u ₃ ( t ) = U_m sin ( m t + 2Aa ) ;

i 2 ^{( t} ) = I m sin ( ^ю t + ^{ф + Аа)} , где U m , I m - амплитудные значения напряжения и тока; ю - угловая частота входного сигнала; ф - угол сдвига фаз между входным напряжением и током. В момент времени, когда напряжение и 3 ( t ) переходит через ноль (момент времени t 1 на рис. 1) МЗ сигналов будут равны: U 11 = U_m sin ( -2Аа ) ; U 21 = U m sin ^{( -Аа )} ; I ii = I m sin⁽ф^-2Аа); 1 2i = I m sin ⁽ Ф — Аа ) .

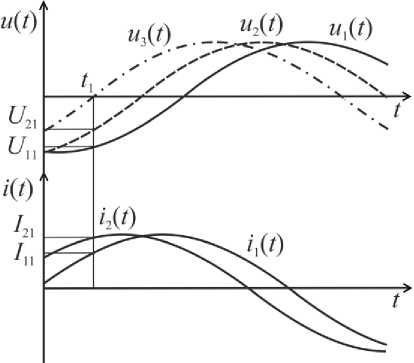
Рис. 1. Временные диаграммы, поясняющие метод

Используя полученные МЗ сигналов, после преобразований можно получить выражения для определения параметров ГС:

• -    среднеквадратические значения напряжения (СКЗН) и тока (СКЗТ)

2 U 1²1

скз /-----;г"

V 4U 21 - U2 ;(1)

' 1221 (4U 221 — U11)+(121Uii — 21iiU 21 )2 2(4UI, - U121).

(2);

• -    активная (АМ) и реактивная (РМ) мощности

U 21 |[( u 1²1 - 2 U 2 ) i 21 + 1 11 U 11 U 21 |

4U 21   U11

Q = ^U 21 ^{( 1} 21 ^U 11 - ¹ 11 ^U 21 )

V 4U221 - U21

Предлагаемый метод можно реализовать с помощью следующей информационно-измерительной системы (ИИС) (рис. 2). В состав ИИС входят следующие блоки: первичные преобразователи напряжения ППН и тока ППТ, фазосдвигающие блоки ФБ1 - ФБ3, осуществляющие сдвиги дополнительных сигналов на угол Да, аналогоцифровые преобразователи АЦП1 - АЦП4, нуль- орган НО, контроллер КОНТ с шинами управления ШУ и данных ШД.

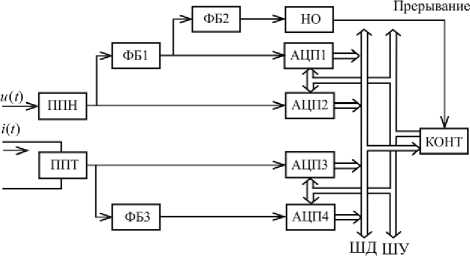
Рис. 2. Схема ИИС, реализующей метод

Одним из видов погрешности, которая может возникнуть при реализации метода, является угловая погрешность фазосдвигающих блоков. Наличие данной погрешности может привести к тому, что углы сдвига фаз ФБ будут различны.

Анализ погрешности реализации метода из-за не идеальности фазосдвигающих блоков. Если считать, что ФБ1 и ФБ2 имеют угол сдвига фазы, соответствующий Да, а угол сдвига фазы ФБ3 в канале тока равен Да-Дв, то МЗ дополнительного тока примет вид 1 21 = I m sin ( ф + Ар-Аа ) . Анализ выражения (1) показывает, что СКЗН будут измерены без погрешности.

Погрешности определения остальных параметров ГС в соответствии с (2) - (4) будут равны:

^ i в =

—-— {sin2 (ф - 2 Аа) + sin (ф + Ав - Аа) х sin Аа х [sin(ф + Ав - Аа) - 2 sin (ф - 2Аа)cos Аа]}2 -1.

YPв =-----[sin(ф + Ав - Аа)cos2Аа - sin Аа

• -    sin ( ф- 2 Аа ) cos Аа ] - cosф.     ^

у_ер = 2 sin ( ф + Ав- Аа ) cos Аа-

• -    sin ( ф- 2 Аа ) - sin ф

Из выражений (5) - (7) видно, что погрешности измерения СКЗТ, АМ и РМ зависят не только от значения угла Дв, но и от угла сдвига фазы ФБ Да и угла сдвига фаз между входным напряжением и током ф. Графики зависимости относительной погрешности измерения СКЗТ и приведенных погрешностей определения АМ и РМ от Да и ф при Дв=0,1°, построенные согласно (5) - (7), показаны на рис. 3-5. Из анализа рис. 3-5 следует, что при небольших значениях угла Да погрешности достаточно малы и при соответствующем выборе значений угла сдвига фазы ФБ ими можно пренебречь практически во всем диапазоне изменения угла ф. При этом минимальные значения погрешностей измерения параметров ГС будут при Аа=90°.

Если считать, что ФБ1 и ФБ3 имеют угол сдвига фазы Аа, а угол сдвига фазы ФБ2 будет равен Аа+Ар, то МЗ дополнительных сигналов будут равны:

U ‘ 1 = U m sin ( - Ар - 2Аа ). U 2 " = U m sin ( - Ар - Аа ).

I fj = I m sin ( ф - Ар - 2Аа). 1 2j = I m sin ( ф- Ав - Аа ) ;                                                                .

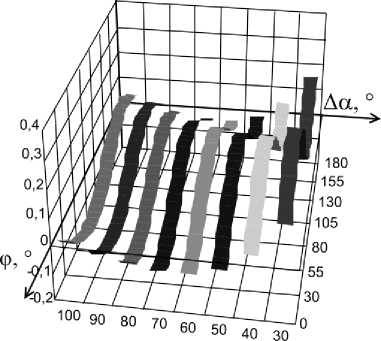
Рис. 3. Графики зависимости 5 i в от Аа и ф

Погрешности определения параметров ГС в соответствии с (1) - (4) будут равны:

⁵ U в

4 sin 2

5 1 в

2sin² ( Аа + Ав )

-1

( Аа + Ав ) - sin² ( 2Аа + Ав )   .    ^

= I                                     х д/ 4sin2 (Аа + Ав)-sin2 (2Аа + Ав)

х { sin² ( ф - Ав - Аа ) [ 4sin² ( Аа + Ав ) - sin² ( 2Аа + Ав ) ] + [ sin фsin Аа -sin ( ф - Ав - 2Аа ) sin ( ф + Ав )] ² } 2 -1.

—

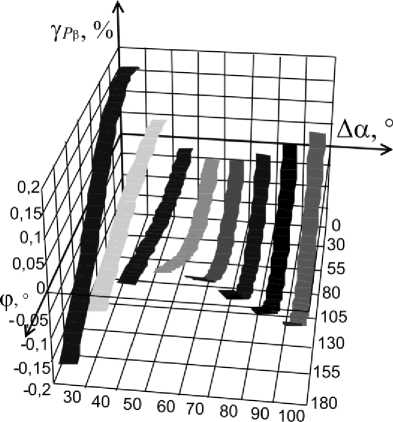
Рис. 4. Графики зависимости у p р от Аа и ф

2|sin ( Аа + Ав )

Y P ^в  4sin² ( Аа + Ав ) - sin² ( 2 Аа + Ав )

х { [ sin² ( 2Аа + Ав ) -2sin² ( Аа + Ав ) ] х х sin ( ф - Ав - Аа ) - sin ( ф - Ав - 2Аа ) х

х sin ( Ав + Аа ) sin ( Ав + 2Аа )} - cos ф . ;

2sin ( Аа + Ав ) sin ф sin Аа

Y Q _в = /                          = - sin ф

4sin² ( Аа + Ав ) -sin² ( 2Аа +Ав ) .

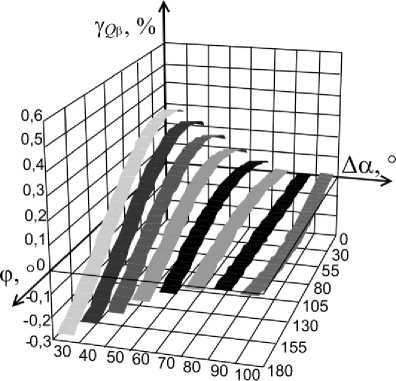
Рис. 5. Графики зависимости у о р от Аа и ф

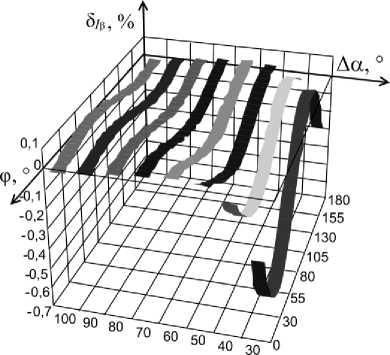
Рис. 6. Графики зависимости 5 i р от Аа и ф

Анализ выражения (8) показывает, что погрешность определения СКЗН зависит только от отклонения угла сдвига ФБ Ар и угла Аа. Из выражений (9) - (11) следует, что погрешности измерения СКЗТ, АМ и РМ зависят еще и от угла сдвига фаз между входным напряжением и током ф. Графики зависимости относительной погрешности измерения СКЗТ и приведенных погрешностей определения АМ и РМ от Аа и ф при Ар=0,1°, построенные в соответствии с (9) - (11),

приведены на рис. 6-8. Анализ графиков, показанных на рис. 6-8, позволяет сделать вывод о том, что погрешности определения параметров ГС существенно зависят от угла Δα. При выборе данного угла в диапазоне значений Δα=70÷100º погрешности не превышают 0,05% при Δβ=0,1º.

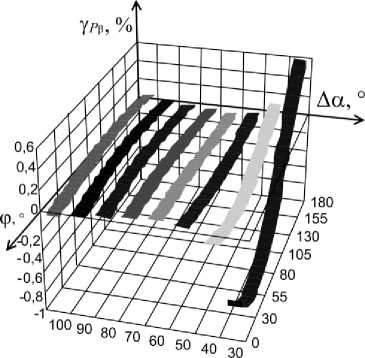
Рис. 7. Графики зависимости γ P β от Δα и φ

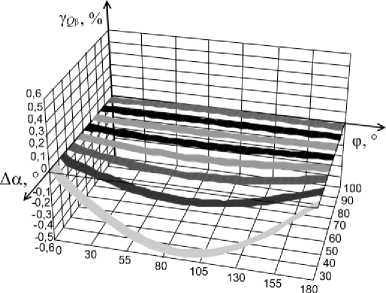
Рис. 8. Графики зависимости γ Q β от Δα и φ

Выводы: реализация разработанного метода определения параметров гармонических сигналов позволяет снизить аппаратурные затраты и сократить время измерения. Проведенный в статье анализ показывает, что погрешность измерения информативных параметров существенно зависит от идентичности используемых для формирования дополнительных сигналов фазосдвигающих блоков. Полученные результаты позволяют определять оптимальные углы сдвига фазы фазосдвигающих блоков в зависимости от требований по точности измерения.

Работа выполнена при финансовой поддержке РФФИ (грант № 16-08-00252 А)