Использование математической модели для оценки оптимальности параметров строительных конструкций
Автор: Щенников В.Н., Люпаев Б.М., Гарина С.В.
Журнал: Инженерные технологии и системы @vestnik-mrsu
Рубрика: Математика, физика
Статья в выпуске: 3-4, 2004 года.
Бесплатный доступ
Короткий адрес: https://sciup.org/14718581
IDR: 14718581
Текст статьи Использование математической модели для оценки оптимальности параметров строительных конструкций
Предлагается способ экономической оценки параметров несущих железобетонных и других композиционных конструкций.
Рассмотрим однокритериальную многопараметрическую выпуклую целевую функцию стоимости железобетонной конструкции
F(x) = ЕС^,...,^) . (1)
Здесь хА ... хп — параметры несущих железобетонных конструкций.
Функция F(x) задана па выпуклом компакте К с Rn со значениями в пространстве вещественных чисел 7? Г т. е.
F(x) :K^R
Задача состоит в нахождении минимума функции Е(т), где хе К.
Имеется достаточно много подходов к решению указанной задачи. Существуют сложные поисковые и оценочные методы [6]. Поисковые универсальнее, но значительно труднее оценочных. Последние позволяют использовать определенные закономерности, характеризующие оптимальные решения. В работах [5; 6] рассматривается оценочный метод проверки оптимальных параметров для строительных конструкций.
Из выпуклой целевой функции выделяются слагаемые, которые с увеличением значения хк возрастают. Обозначим их как F^X]^ . Слагаемые функции, которые с повышением значения х^ убывают, обозначим FCx^), а не меняющие значение с изменением х^ — Рйк.
Оптимальному значению F(xA) свойственно равенство групп F(x^) и F(,x0 или достаточно малое их отклонение от равенства па допустимую величину с^, обычно принимаемую равной 0,01^ [51.
Р(хк + сй) - Р(.х^У,Р(х^ + с0 - Р(хкУ(2)
Оптимальность решения оценивается коэффициентом экономичности Э, который находится по формуле [5J
Э = Е(х^) / Е(х^)|. (3)
Оптимальному значению соответствует значение Э = 1. Предлагаемая методика оценки оптимальности решений включает не только вычисление коэффициента экономичности Э, но и учет степе-+ — ни влияния групп FU0 и F + " где m, т — коэффициенты влияния для + — F(x0 и F(x0 ; Дх^ — приращение параметра хк. С учетом коэффициентов интенсивно-+ — сти тит формула (3) запишется как + - где W W — обобщенные группы. Величина х^пт находится по формуле 4™ -4к-,к = Х..,п. (6) При Э = 1 решение оптимальное, при Э < 1 оптимум достигается увеличением х^, при Э > 1 — уменьшением х^. Эта методика проста в применении. Недостаток ее состоит том, что для более сложных видов функций поиск экстремумов значительно усложняется. Таким образом, возникает необходимость использования других методов и подходов к поиску оптимальных значений функций. В современной теории выпуклого программирования [3; 7] разработало множество численных методов для задач оптимизации. Приведем некоторые определения и теоремы из теории выпуклого программирования, которые потребуются в дальнейшем. Определение 1 [8]. Подмножество К в R” называется выпуклым, если (1 - Л)х + Ху е К для любых хе К, уеКи 0 < X < 1. Определение 2 [8]. Функцию F(x), определенную на выпуклом множестве К, называют выпуклой, если для любых х, у е К всех Хе [0,1] выполняется неравенство F(Xx + (1 - Х^ < ХРЫ + (1 - XW. (7) Если для любого X е [0, 1] неравенство строгое, то функцию F(x) называют строго выпуклой. Теорема 1 [7]. Для того чтобы точка х0 была точкой минимума строго выпуклой функции F(x^ во всем пространстве, необходимо и достаточно, чтобы OedF(xo) (8) Здесь 9F(x0) — субдифференциал функции Fix) [8]. Условие (8) теоремы 1 равносильно системе ^^^^ = 0, * = й. (9) Составим далее систему дифференциальных уравнений потенциального типа: ^= ^ЫР й=^ (10) d t ^^k Теорема 2 [4]. Если градиент функции F^,..., хп) обращается в пуль в единственной точке, являющейся оптимальной точкой этой функции, и выполняется неравенство ||gradF(x)|| > a-j > 0 при У -> +™ , то любая интегральная кривая х = х(О системы (10) обладает свойством х(О ->Xq При ^ —> +оо , т. е. интегральная кривая х = х(О может достигать оптимальной точки за конечное время. Следствие [4]. Если функция F(x^, ..., х„) достигает в некоторой точке х0 ч (хщ, ..., хп0) минимума и если в достаточно малой ее окрестности градиент этой функции не обращается в пуль нигде, за исключением самой точки, то точка (х^, ..., хп0) будет асимптотически устойчивой. Таким образом, положение равновесия Xj = Хю, ...,хп = x„q системы (10) совпадает с точкой минимума, найденной из системы (9). Из изложенного следует алгоритм экономической оценки параметров несущих железобетонных и других композиционных конструкций: 1. Составляется выпуклая целевая функция относительной стоимости железобетонной конструкции F(x) = = Ffx^ ..., xn) . допускающая непрерывные частные производные по переменным хр ..., Ху. 2. Составляется алгебраическая система вида (9). 3. Находится решение системы (9), т. е. определяется точка Xq = — ( X | Q , ..., X пq ) 4. Составляется система дифференциальных уравнений потенциального типа: 5. Устанавливается асимптотическая устойчивость в целом решений системы (9) относительно х0 = (х^, ..., хи0). Если окажется, что х0 асимптотически устойчиво в целом, то х0 является оптимальным. dx, ВР(хА, х ) — =--—_дш h = 1, п. dt dxk Тем самым получаем искомое х0: Р(х0) — наименьшее (оптимальное) значение функции F(x) = F(xt, ..., х„) Примечание 1. Алгоритм допускает упрощение в части первого пункта. В нем можно заменить условие выпуклости условием [1; 4] ||grad F(x)|| > a > 0. Примечание 2. Данный алгоритм приводит к оптимальному значению F(x) только в том случае, когда решение является неотрицательным, т. е. x.q > 0, / = 1, п. Если же решение системы(9) окажется xq< 0 (х;о < 0, / = 1, п) , то заданную задачу следует решать как задачу оптимизации при наличии дополнительных ограничений на переменные х3\]=Ы [3; 7; 8]. Примечание 3. Преимущество данного алгоритма состоит в том, что не требуется решения системы (10). Алгоритм значительно упрощается, если правая часть системы (10) допускает линейное приближение. В этом случае для установления асимптотической устойчивости х0, необходимо проверить условия Рауса — Гурвица и воспользоваться теоремой Ляпунова об асимптотической устойчивости по первому линейному приближению [2]. Целевую функцию качества можно упростить так, чтобы система (10) получалась линейной. Оценка погрешности при этом определяется в соответствии с формулами, полученными в работе [9]. При расчете экономической оценки параметров железобетонных и различных композиционных конструкций нередко функция стоимости F(xj, ..., хп) зависит от достаточно большого количества независимых переменных, поэтому система (9) практически неразрешима. Решим эту задачу в предположении, что функция F(x) допускает представление Fto = №°)+ 24 щ-4)Л+- ■ к=л& L а*1 F(x°), (И) где х = (хь ..., х„) , х° = (х?, .... х°) - начальная точка. Система (9) в этом случае примет вид уравнений, левые части которых имеют степенные ряды. Для того чтобы разрешить ее, ограничимся в разложении (11) членами второго порядка. Тогда она будет системой п линейных уравнений с п неизвестными. Функцию с ограниченным числом членов ряда обозначим как Ф(хь ..., хп) Тогда ФСг ।,..., хп) = F(x°) + (^ - х?) -Д- + • ■ ■ dJtj Следовательно, если нулевое решение системы (15) асимптотически устойчиво, то точка х0 = Ст10, ..., х„0) является точкой минимума. Чтобы выполнялось условие (16) теоремы 3, необходимо и достаточно проверить выполнимость критерия Рауса — Гурвица [2], т. е. справедливость неравенств С учетом всех числовых коэффициентов перепишем выражение (12) в виде п ФОф ..., х„) = ай + 26^ + i=i + ^CyX^j. (13) ij=^ Если симметрическая матрица С = [ci;] будет строго определенно-положительной [7], то функция (13) с ограниченным числом членов ряда будет также строго выпуклой. Исследуем систему (10) па устойчивость. В нашем случае это линейная неоднородная система с постоянной матрицей. Запишем ее как — = Ах + В. (14) at где А = [«у ] — постоянная пхп матрица, х = colon (xt, ..., хп\ В = colon (йр йп), bj = const, i = 1, п Путем замены ^к — ^к + ^к0' ^ ^ й (здесь хк — новые функции) перейдем к однородной системе ^ = Ах. (15) Теорема 3 [2]. Линейная однородная дифференциальная система (15) с постоянной матрицей А асимптотически устойчива тогда и только тогда, когда все характеристические корни Л;=Я7(Л) матрицы А имеют отрицательные вещественные части: Re Лу (А) < 0, / = 1Гй. (16) ^3 й2 Й1 йо 0 0 й5 а4 йз ^2 Д1 й0 Согласно изложенному алгоритму найдем оптимальные параметры монолитного железобетонного перекрытия. За критерий оптимальности примем относительную стоимость перекрытия, описываемую формулой Р(х^х2,хг) = х1 + х2 + х3 +-------. (18) ^2^3 где F — относительная стоимость перекрытия; х^ — высота сечения плиты; х2 — высота сечения второстепенной балки; х3 — высота сечения ригеля. х° = (1,41; 0,84; 1) — начальная точка. FСс), х2, х3 ) = 4,094 + 0,40 К^ -1,41) - - 0,005(х2 - 0,84) + 0,156(^3 -1) + + |о,849а1 -1,41)2 +0,713^ -1,41)х х (х2 - 0,84) + 0,599(xt - 1,41)(д3 -1) + +12,393(^2 - 0,84)2 + 1,005(^2 - 0,84) х х(х3-1) + ^1,689(х3-I)2 + ... (19) Функция Ф(лф.Х2,^з) имеет вид Ф (xi,x2,x3) = 8,444-1,994X1 -4,025^2 -- З,222х3 + 0,425xf + 1,197х| + + 0,846х3 + 0,713Х]Х2 + O,599xix3 + + 1,005x2X3. (20) Докажем выпуклость функции (20). Рассмотрим квадратичную форму С = 0,425х2 + 1,197^ + 0,846х3 + + 0,713xjX2 + ОДЭЭх^з + 1,005х2х3. (21) Ее матрица имеет вид "0,425 0,356 0,299) 0,356 1,197 0,502 (22) 0,299 0,502 0,846 Эта матрица положительно определенная, так как Aj > 0, Д2 > 0, Д3 > 0 (критерий Сильвестра [2]). Следовательно, квадратичная форма (21) выпукла и выпукла функция (20). ---— 0,849x1 + 0,713х2 + + 0,599хз -1,994 = О, ЭФ — = 0,71 Зх|+2,393X2 + (23) и^2 + 1,005х3 -4,025 = О, ЭФ — = 0,599х! + 1,005х2 + Эх3 + 1,689x3 -3,222 =0. Решением системы (23) является точка х0 = (0,765; 1,022; 1,028). = -0,849xi -0,713x2 -dt -0,599хз+1,994, ^ = -0,713xt - 2,393x2 " (24) - 1,005х3 + 4,025, = -0,599x1 - 1,005х2 - dt 1 " Путем замены Xj = X) + 0,765, х2 = х2 + 1,002, х3 = х3 +1,028 преобразуем систему (24) к виду =-0,849X1 -0,713x2 -0,599х3, dt = -0,713^ -2,393х2 -1,005х3, (26) dt ^ = -0,599xi - 1,005х2 - 1,689х3. dt 3 Исследуем нулевое решение системы (26) на асимптотическую устойчивость. Проверим условие Рауса — Гурвица. Если оно выполняется, то решение Xi = х2 = х3 = 0 асимптотически устойчиво, а значит, точка xt = 0,765, х2 = 1,022, х3 = 1,028 асимптотически устойчива и является точкой минимума функции (18) [2]. Составим характеристическое уравнение для системы (26): Л3 + 4,9Л2 + 5,5Л + 1,7 = 0. Следовательно, матрица Гурвица имеет вид 4,9 1,7 0 5,5 0 Д2 - 4,9 1,7 О 4,9 , Д, = 4,9 > 0, V 1 >0, Д3=1,7Д 5,5 3 Условия Гурвица выполнены, значит, X! = 0,765, х2 = 1,022, х3 = 1,025 является точкой минимума. - 1,689х3 + 3,222.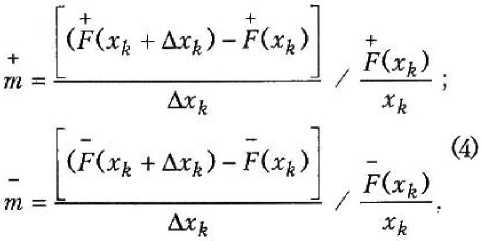
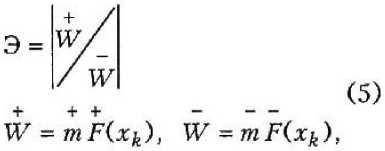
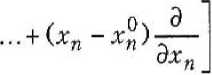
Й1
й0
0
д2 -
й3
й2
Й1
>0,...,
й5
й6
й3
(17)
a-i Qq 0 0 0 0
Список литературы Использование математической модели для оценки оптимальности параметров строительных конструкций
- Бобылев Н. А. О функциях Ляпунова и задачах на глобальный экстремум/Н. А. Бобылев//Автоматика и телемеханика. 1979. № 11. С. 5 -9
- Демидович Б. П. Лекции по математической теории устойчивости/Б. П. Демидович. М.: Наука, 1967. 472 с.
- Демьянов В. Ф. Введение в минимакс/В. Ф. Демьянов, В. Н. Малоземов. М.: Наука, 1972. 368 с.
- Зубов В. И. Теория оптимального управления судном и другими подвижными объектами/B. И. Зубов. Л.: Судостроение, 1966. 352 с.
- Люпаев Б. М. О качественных оценках оптимальности технических решений/Б. М. Люпаев, C. В. Гарина//Современные проблемы строительного материаловедения. Воронеж, 1999. С. 259 -263.
- Потапов Ю. Б. Композиционные строительные конструкции/Ю. Б. Потапов, В. П. Селяев, Б. М. Люпаев. М.: Стройиздат, 1984. 100 с.
- Пшеничный Б. Н. Выпуклый анализ и экстремальные задачи/Б. Н. Пшеничный. М.: Наука, 1980. 320 с.
- Рокафеллар Р. Выпуклый анализ/Р. Рокафеллар. М.: Мир, 1973. 470 с.
- Щенников В. Н. Оценки погрешности линеаризации относительно части и всех фазовых переменных/В. Н. Щенников, Е. В. Щенникова//Дифференц. уравнения. 2001. Т. 37, № 1. С. 132 -133.


