Использование метаповерхности для детектирования дробных топологических зарядов при разных длинах волн

Метаповерхности – это ультратонкие планарные дифракционные оптические элементы, способные выполнять различные оптические преобразования светового пучка. Метаповерхности используются в различных областях, таких как создание волновых фронтов с произвольным распределением фазы [1 – 3], металинзы и фокусаторы [4, 5], голография [6, 7], абсолютное поглощение света [8, 9], в задачах инженерии волновых фронтов [10 – 13], и других. Одним из перспективных направлений использования метаповерхностей является кодирование и детектирование топологических зарядов. Например, в [14] предложен метод создания металинзы для генерации различных топологических зарядов (ТЗ), причем металинзу можно растягивать, меняя результирующее поле на ее выходе и изменяя таким образом топологический заряд. В [15] предложен метод проектирования металинз, состоящих из двух поверхностей, для манипуляции топологическим зарядом выходного пучка. А в [16] разработаны металинзы для генерации универсальных спиральных пучков (VSB), полученных за счет комбинации самофокусируемых пучков Эйри и фазовой функции металинзы. Известны также работы по детектированию топологических зарядов. Например, в [17] авторы использовали азимутально-квадратичную фазу, полученную с помощью метаповерхности, для детектирования оптических вихрей. В [18] предложена методика создания метаповерхностей, одновременно генерирующая несколько топологических зарядов с по-

мощью метаповерхности в виде наносита. В [19] авторы предложили способ создания металинз для генерации цилиндрических векторных пучков или пучков с заданным топологическим зарядом в зависимости от освещающего её поля. Известны и другие работы в области детектирования оптических вихрей [20]. Во всех перечисленных работах речь идет о целочисленных топологических зарядах. Дробные вихри используются намного реже, и чаще идет речь об их генерации. Например, в [21] авторы использовали дробные топологические заряды 1/3, –1/3 для создания плазмонов со стоячей волной, что позволило им создать микроскоп, основанный на флуоресценции, со 100 нм разрешением.

Работы, в которых разрабатываются металинзы (или другие дифракционные оптические элементы) для детектирования дробного топологического заряда, встречаются намного реже. В [22] авторы разработали способ измерения дробного топологического заряда. Для его измерения использовался фотодетектор с одним пикселем, на который свет попадал после интерферометра Маха–Зендера, в котором использовалось отражение света от вращающейся пластины. Таким образом была использована коррекция дробной части топологического заряда с помощью эффекта Доплера. Авторы измеряли топологический заряд в широком диапазоне, от 4,3 до 10,3, однако для его измерения необходимо использовать механические подвижные части и вращающийся элемент. В [23] была разработана и промоделирована металинза для детектирования дробного ТЗ в диапазоне от 0 до –2. При этом в ней не были использованы какие-либо подвижные части, приводимые в движение для ее работы. Однако те расчеты были выполнены для одной длины волны света.

В данной работе рассматривается подобная металинза для работы в некотором диапазоне длин волн. Поскольку металинза состоит из субволновых дифракционных решеток и не используются резонансные явления на наностолбиках, она имеет работоспособность в диапазоне длин волн от 0,56 до 0,7 мкм, где, как показало моделирование, можно детектировать как топологический заряд падающего пучка, так и длину волны света одновременно.

Моделирование в ближней зоне

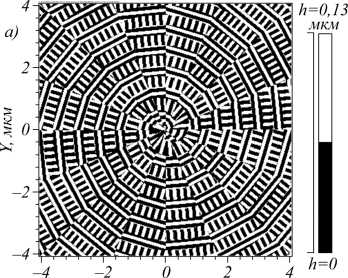
На рис. 1 приведен расчетный рельеф металинзы для детектирования дробных топологических зарядов с ТЗ m =–0,5. Преобразование волнового фронта металинзой представляет собой матрицу

R (ф) =

cos ф - sin ф

- sin ф

- cos ф

умноженную на пропускание спиральной пластинки e^{m ф} с порядком n =-1,5 и функцию пропускания сферической линзы exp ( - ikr ² / (2 f ) ) , здесь угол ф - угол поворота вектора электрического поля по часовой стрелке или против неё. Фокусное расстояние линзы равно f = λ = 0,633 мкм. Она имеет размер 8×8 мкм (364×364 отсчетов) и создана из 16 секторов аналогично металинзе в работе [23]. Глубина рельефа металинзы в аморфном кремнии составляет h = 0,13 мкм, её подложка имеет показатель преломления n = 1,5. Пока-

затель преломления аморфного кремния был принят n = 4,352+0,486 i , что справедливо для указанной выше центральной длины волны света, чтобы продемонстрировать особенности работы металинзы без добавления других эффектов, в частности, дисперсии мате-

риала, в ее работу. Металинза составлена из дифракционных решеток с периодом 0,22 мкм, ширина канавок и ступенек одинаковая и равна 110 нм.

X, мкм

Рис. 1. Рельеф металинзы, рассчитанной на детектирование топологического заряда m = –0,5 для длины волны света λ = 0,633 мкм

Заметим, что в некоторых работах, например, в [24], предлагается аналогичные металинзы создавать с помощью субволновых решеток с непрерывным изгибом линий. Но такой подход не является технологичным, так как в этом случае период решеток может существенно изменяться, что приведет к ошибкам изго-

товления и, как следствие, к удорожанию производства. Кроме того, из-за изгиба линий период решеток может увеличиться до того, что перестанет быть субволновым, или наоборот, станет слишком малым, что увеличит аспектное соотношение и опять-таки увеличит стоимость изготовления.

При падении на данную металинзу света с левой круговой поляризацией и вихрем с ТЗ m = –0,5, в фокусной плоскости формируется круглое световое пятно (что было получено в [23]) (рис. 2 а, б ):

( , , „ , kr2 ) exp 1-1,5iф - 0,5iф - i -2f Ix

( cos ф

xl •

J- sin ф

- sin ф 11 1

- cosфJI -i

= exp I - iф -

■ kr ² J^{( 1} J i .

2 f Л i J

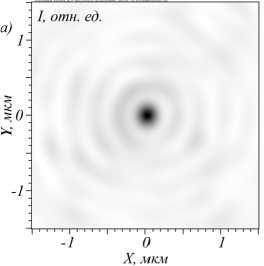
Ix+Iy, отн. ед.

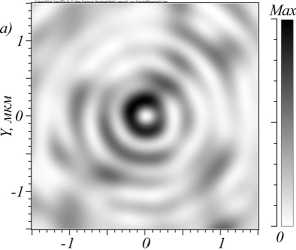
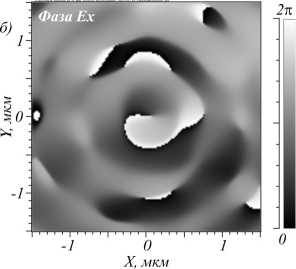
Рис. 2. Интенсивность света в фокусной плоскости металинзы (а) и фаза проекций электрического вектора Ex, Ez (б, в)

В соответствии с формулой (1) в центре должно быть кольцо, так как присутствует вихрь (рис. 1б), однако на рис. 1а изображено круглое фокусное пятно. Причина этого в том, что максимум интен- сивности находится в Ez-компоненте поля, а поперечные компоненты выражены не так сильно (рис. 3). В то же время вихря в проекции поля Ez нет (рис. 2в).

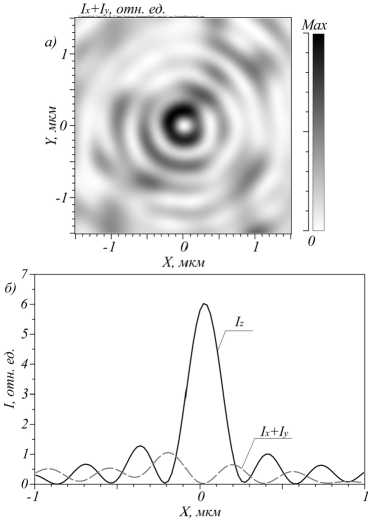
Рис. 3. Интенсивность поперечных компонент (а) и сечение вдоль оси X поперечных и продольной компонент электрического поля в фокусной плоскости

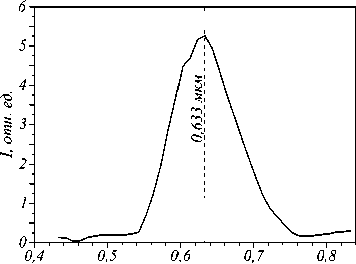
Работоспособность данной металинзы сохраняется в некотором диапазоне длин волн. На рис. 4 показана зависимость интенсивности в фокусном пятне на оптической оси от длины волны падающего света в диапазоне от 0,433 до 0,833 мкм с шагом 10 нм. Данное моделирование было проведено методом FDTD в коммерческом программном пакете FullWave (RSoft – LightTec). Сетка разбиения вдоль всех трех осей была выбрана λ/30, размер области моделирования составил 8,2×8,2×1,933 мкм, шаг дискретизации по времени был выбран как максимальный устойчивый и равен cT = 0,0113 мкм, где c – скорость света в вакууме.

\мкм

Рис. 4. Зависимость интенсивности в фокусном пятне на оптической оси от длины волны падающего света

Из рис. 4 видно, что данная металинза работает хорошо лишь на небольшом участке длин волн, в диапазоне от 0,56 до 0,7 мкм. В нём интенсивность меняется приблизительно в 3,3 раза. Расчетная длина волны света равна λ =633 нм, на эту длину волны света рассчитана спиральная зонная пластинка, которая встроена в металинзу, и высота субволновых дифракцион- ных решеток для преобразования поляризации падающего поля. На этой длине волны и достигается максимум интенсивности.

Метаповерхность для дальней зоны

Для того, чтобы метаповерхность работала в большем диапазоне длин волн, следует выбрать работу в дальней зоне. На рис. 5 показан рельеф металинзы для дальней зоны. Эта металинза не содержит фокусирующего элемента в своей структуре и рассчитана на работу с ТЗ –1,5:

R ( Ф ) =

^ cos ( ax + m ф ) - sin ( ax + m ф )

- sin ( ax + m фр - cos ( ax + m ф )

где коэффициент α =3,4 отвечает за отклонение левой и правой круговых поляризаций, выходящих из металинзы, вдоль оси X [25], а m = 1,5 – константа, отвечающая за расчетный топологический заряд падающего поля, она определяет наклон решеток в различных областях при обходе метаповерхности по окружности.

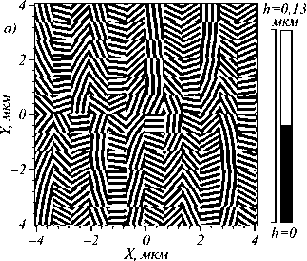
Рис. 5. Металинза для работы в дальней зоне с дробным ТЗ

При прохождении через такую металинзу света с правой круговой поляризацией выходной пучок отклоняется влево [25], при этом интенсивность нулевого порядка почти равна нулю. Для получения распределения интенсивности поля в дальней зоне прохождение света через метаповерхность рассчитывалось с помощью FDTD-метода и результаты его расчета аккумулировались на расстоянии 0,3 мкм за ней, а далее производился расчет компонент вектора электрического поля интегралом Рэ-лея–Зоммерфельда на расстоянии 100 мкм. Такая комбинация давала возможность уменьшить время расчета без ущерба для его точности. На рис. 6 показана зависимость координаты X центра светового пучка, расположенного в плоскости наблюдения на расстоянии 100 мкм после металинзы.

При длине волны света λ = 0,433 мкм координата X пучка равна –24,2 мкм, при λ = 0,833 мкм центр пучка расположен в X = –50,3 мкм. В рассмотренном же диапазоне от λ = 0,56 мкм до λ =0,7 мкм центр пучка в плоскости наблюдения сдвигается вдоль оси X на 9 мкм, от X = –31,9 до –40,9 мкм. То есть из рис. 6 можно сделать вывод, что за счет почти линейного смещения координаты центра пучка (выходного угла луча) от длины волны света можно сделать однозначный вывод о падающей длине волны. Так же моделирование показывает, что нулевой порядок практически отсутствует при расчетной длине волны света. При изменении длины волны как в большую, так и в меньшую сторону на оптической оси появляется кольцо, которое становится постепенно все ярче с отклонением длины волны от расчетного значения.

Интерес представляет не только работоспособность металинзы при различных длинах волн, но и детектирование дробных топологических зарядов. На рис. 7 показаны зависимости интенсивности в пучке и его координата Y от топологического заряда падающего пучка, который изменяется в диапазоне от –2 до –1. Расчетное значение, для которого проектировалась метаповерхность, равно –1,5.

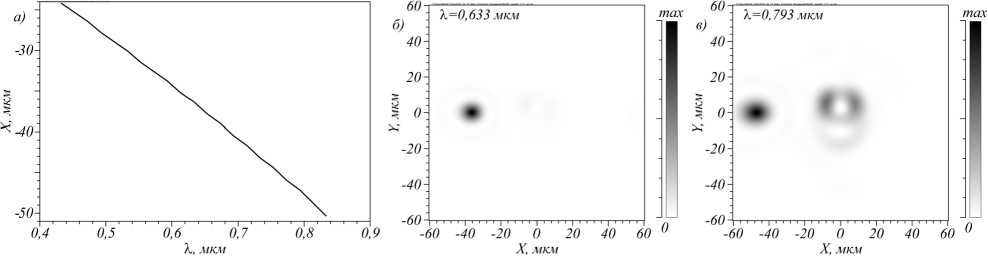
Рис. 6. Зависимость координаты X центра отклоненного пучка в плоскости наблюдения от длины волны падающего излучения на металинзу (а) и пример интенсивности в плоскости наблюдения при длине волны света 0,633 мкм (б) и 0,793 мкм (в). Расстояние до плоскости наблюдения было взято 100 мкм

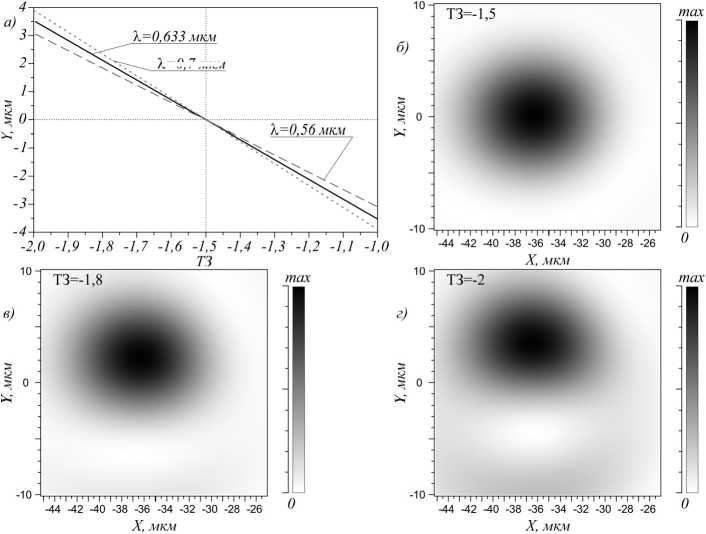
k=0.7 мкм

Рис. 7. Зависимость координаты Y максимума интенсивности в плоскости наблюдения от ТЗ падающего пучка (а), и распределение интенсивности в плоскости наблюдения для различных ТЗ: –1,5 (б), –1,8 (в), –2 (г)

Из рис. 7 видно, что изменение ТЗ от –2 до –1 при λ = 0,633 мкм приводит к изменению координаты Y максимума интенсивности в диапазоне от Y =3,5 мкм до Y = –3,5 мкм. При этом моделирование показало, что центр максимума интенсивности вдоль оси X расположен в координате X = –36,3 мкм и не зависит от ТЗ. Также из рис. 7 видно, что чем больше длина волны, тем больше изменение положения максимума интенсивности пучка в поперечной плоскости, вдоль оси Y. При изменении длины волны с 0,56 до 0,7 мкм величина сдвига максимума интенсивности в плоскости наблюдения на расстоянии 100 мкм от металинзы составляет 27,8 % (с X = 3,05 до X = 3,9 мкм при TC = –2). При этом зависимость сдвига максимума интенсивности в рассмотренном диапазоне изменения топологического заряда практически линейная. То есть величина дробной части топологического заряда вполне может быть оценена настолько точно, насколько возможно измерить положение максимума интенсивности пучка вдоль оси Y для используемой длине волны. А длину волны λ для этого можно оценить по координате X, так как зависимости от ТЗ у неё нет.

На рис. 8 показана зависимость максимума интенсивности от величины ТЗ для трех разных длин волн.

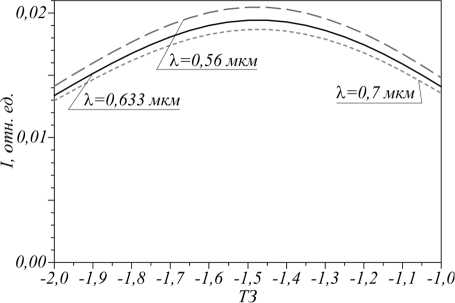
Рис. 8. Зависимость максимума интенсивности в пучке от топологического заряда при различных длинах волн

Как можно понять из рис. 8, максимум интенсивности приходится на расчетный дробный ТЗ = –1,5 и слабо зависит от длины волны света: при уменьшении λ до 0,56 мкм интенсивность возрастает примерно на 5,1…5,7% (по всему диапазону ТЗ), а при увеличении λ до 0,7 мкм – уменьшается на 3,1…3,8%. При этом изменение ТЗ от –2 до –1,5 приводит к увеличению интенсивности на 30%. То есть изменение длины волны света несущественно уменьшает интенсивность максимума. Из сравнения графиков на рис. 8 и 4 следует, что отсутствие фокусирующей линзы в структуре метаповерхности сильно расширяет диапазон возможных длин волн. Это объясняется тем, что для фокусировки света в металинзу встраивалась зонная пластинка. Чем дальше её зоны от центра, тем они хуже фокусируют свет, или наоборот, мешают фокусировке: с изменением длины волны света из-за несоответствия ширины зон Френеля длине волны набегает ошибка в формировании фазового фронта, что ухудшает работу металинзы несмотря на то, что работоспособность субволновых решеток сохраняется. По этой причине при необходимости использовать метаповерхность в некотором диапазоне длин волн целесообразна работа в дальней зоне.

Заключение

В работе продемонстрирована возможность использования метаповерхности для детектирования дробных топологических зарядов. Показана возможность работы металинзы как в ближней, так и в дальней зоне. Моделирование показало, что при работе в ближней зоне (фокусное расстояние равно 0,633 мкм) металинза работает хорошо лишь на небольшом участке длин волн. В диапазоне от 0,56 до 0,7 мкм интенсивность меняется приблизительно в 3,3 раза. В то же время при работе в дальней зоне в том же диапазоне длин волн интенсивность в центре пучка изменяется лишь на 30%. При этом по смещению интенсивности вдоль осей X и Y можно оценивать длину волны света и дробный топологический заряд. Например, при изменении ТЗ от –2 до –1 фокусное пятно смещается вдоль оси Y приблизительно на 7 мкм, а при изменении длины волны света от 0,56 до 0,7 мкм максимум интенсивности смещается на 9 мкм вдоль оси X. Эти данные справедливы для плоскости наблюдения на расстоянии 100 мкм за метаповерхностью. Моделирование также показало, что зависимости положения вдоль оси X максимума интенсивности от ТЗ в рассмотренном дробном диапазоне ТЗ нет, что позволяет оценить как длину волны, так и дробную часть ТЗ по расположению максимума интенсивности в координатах X и Y в плоскости наблюдения.

Работа выполнена при поддержке Российского научного фонда (грант 23-12-00236) в частях «Моделирование в ближней зоне», «Метаповерхность для дальней зоны», а также при поддержке Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН в частях «Введение», «Заключение».