Использование метода adaptive threshold в системе технического зрения

В настоящее время практически во всех сферах деятельности человека проходит глобальная информатизация, что накладывает свой отпечаток на устоявшиеся бизнес процессы и технологии. В подавляющем большинстве случаев такие нововведения позволяют добиться повышения эффективности работы той или иной компании, производства. Подобные изменения коснулись и производственных линий, автоматизация которых возможна с использованием роботизированного оборудования, неотъемлемой частью которого является система технического зрения (СТЗ). Основой этой системы является эффективный алгоритм определения контуров изображений.

Учеными из разных стран разработано большое количество различных алгоритмов, которые позволяют решить проблему обнаружения границ образов. У каждого из них есть положительные и отрицательные стороны. В современных же реалиях больше всего востребованы алгоритмы, являющиеся наиболее универсальными. Одним из них является метод Adaptive Threshold. Благодаря адаптивному подходу к расчету порога яркости пикселя, этот метод позволяет наиболее гибко подходить к выделению тех групп точек, которые находятся именно на границе образа.

Для того чтобы понять принцип работы данного метода, необходимо рассмотреть его математическое описание.

Пусть I ( x , y ) представляет собой исходное изображение, которое будет использоваться для адаптивной пороговой обработки. G ( x , y ) – это нормализованное значение градиента изображения I ( x , y ), которое рассчитывается по формуле:

, Vl(x,y\

6(^m^H (1)

Данный метод отличается от других тем, что использует адаптивный порог ( T ( x ; y )) для каждого пикселя исходного изображения. Исходя из этого, получим следующую формулу для бинаризации изображения [2, с. 469]:

1,если/(х,у)>7(х,у) О,если /(х,у)<Г(х,у)

В данном случае I(x,y) и T(x,y) являются двумерными поверхностями (2D), которые пересекаются в позиции c={(x,y)| I(x,y)=T(x,y)} [2, с. 469] опираясь на полученное выражение следует считать, что с будет находиться в тех местах, где находится граница образа на исходном изображении. Это означает, что раз T(x,y) – правильная пороговая поверхность, то значение ∫сG(x,y)dH1(x,y)/C (где H является хаусдорфовой мерой для C, а C – количество граничных точек объекта) будет максимальным. Данный факт позволяет преобразовать функцию T к функциональному простран- ству Ω по следующей формуле:

min Г/^с/нЧ^й/С

Ml J X 1 V '

где, F(T) – это первая производная от T и F(T^ = -G(x,y\(x,y^ec [2, с. 469]. Эта объектная функция достаточно сложная. Чтобы упростить ее, необходимо вы- делить регуляризацию в отдельную функцию. В этом случае изначальная функция примет вид:

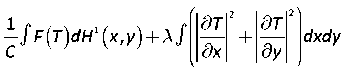
где, λ – параметр регуляризации. Дальнейшая мини-

мизация выражения (4) сводится к решению следующего уравнения Пуассона:

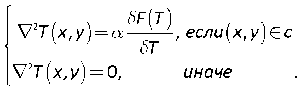
В данном выражении α=1/2 λ . Поскольку F ( T ) касается c , то F ( T ) может быть записан как F ( x ( T ), y ( T )) по правилу цепи:

Данный алгоритм работает достаточно просто. На входе поступает исходное изображение ( I ). Объявляются два цикла, вложенные друг в друга, счетчики которых перебирают все значения по ширине ( x=0; x(I); x=x+1) и длине (y=0; y(I); y=y+1) изображения соответственно. После перехода к очередной точке изображения программа определяет значение адаптивного порога для бинаризации (T(x,y)). После чего проверяется условие I(x;y)>T(x;y), и если оно истинно, то точке результирующего изображения присваивается значение 1, во всех остальных случаях – 0. Таким образом алгоритм обрабатывает все точки изображения и формирует результат.

Благодаря особенностям этот метод может применяться для реализации СТЗ в робототехнике, для обнаружения деталей на конвейерных линиях, при выделении контуров изображений на аэро и космических снимках. Такая универсальность позволяет выделять границы образов даже на сильно загруженных изображениях, при этом границы отдельных объектов остаются точными и полными.

Для оценки универсальности работы рассматриваемого метода была сделана выборка изображений с различными

6T ' 6T v 6T

6T dx

6T dy

Обращаем внимание на то, что здесь T – функция, δT –

измененная мы имеем:

функция T и δT=dI-dT [2, с. 470]. Таким образом,

показателями, а также различным количеством длинных и коротких границ, количеством шума и степенью затененности. Первое из рассматриваемых изображений содержит множество небольших по размеру объектов. В результате на изображении присутствует большое количество границ (рис. 2).

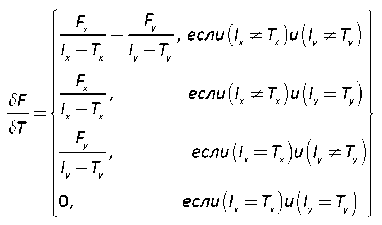
Данное выражение позволяет рассчитать пороговое

значение яркости для бинаризации каждого пикселя, что делает алгоритм применимым для большего числа различных изображений [2, с. 470].

Если обобщить математическое описание нахождения порогового значения, то общий алгоритм работы метода можно изобразить в виде блок-схемы (рис.1):

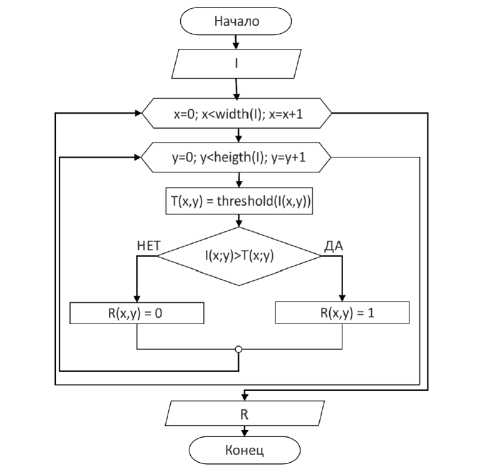
Рис. 1. Алгоритм работы метода Adaptive Threshold

Рис. 2. Исходное изображение с большим количеством границ и мелких деталей

Обработка подобных образов является достаточно сложной. Несмотря на это, после обработки данного изображения алгоритмом Adaptive Threshold были получены следующие результаты (рис.3).

Рис. 3. Результат обработки первого исходного изображения

После обработки на первом тестовом изображении видны границы даже мелких деталей, несмотря на это присут- ствует большое количество ненужных артефактов, которые образовались из-за наличия шероховатости поверхностей. Эти погрешности имеют незамкнутые контура, что позволит впоследствии убрать их с изображения.

Во втором случае имеется контрастный фон, но при этом имеется большое количество тонких и коротких граней, что заметно усложняет процесс обнаружения (рис. 4).

Рис. 4. Исходное изображение с высоким контрастом и большим числом тонких граней

После обработки этого изображения были получены следующие результаты (рис.5).

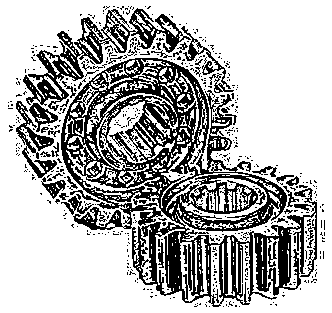
Рис. 5. Результат обработки контрастного изображения с большим количеством узких граней

Несмотря на ореол вокруг образа, связанного с наличием шума на исходном изображении, в результате были выделены контуры каждого зубца шестерней, как внутренних, так и наружных.

Ниже представлено последнее изображение, наиболее подходящее для выделения контуров. Деталь контрастна на фоне, что делает контур наиболее четким (рис. 6).

Рис. 6. Исходное изображение с минимальным количеством помех и искажений

В результате обработки данного изображения были выделены грани деталей, а также небольшие дефекты на ее поверхности (рис. 7). Такие результаты были достигнуты за счет отсутствия дефектов исходного изображения.

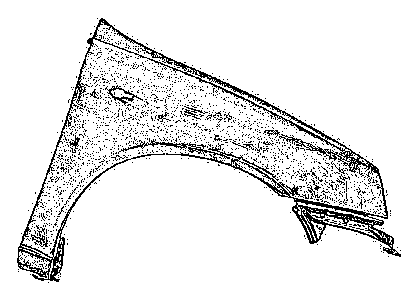
Рис. 7. Результаты обработки изображения, на котором присутствует минимальное количество дефектов

Основываясь на полученных результатах обработки последнего изображения, можно провести два эксперимента. Для первого из них добавим на исходное изображение большое количество шума, которое будет подчиняться нормальному распределению (рис.8).

Рис. 8. Исходное изображение с большим количеством шума

В результате обработки было получено изображение со слабо отличимыми контурами, что неудовлетворительно с точки зрения распознавания образов (рис.9).

Рис. 9. Результат обработки сильно зашумленного изображения

Для проведения второго эксперимента требуется затенить изображение, чтобы получить менее контрастный фон (рис. 10).

После всех проведенных испытаний, можно считать, что данный результат обработки является наилучшим (рис. 11). Такого эффекта удалось достичь за счет перекрытия тенью большого числа таких искажений, как шум. В результате чего адаптивный порог мог рассчитываться более точно и

Рис. 10. Исходное изображение с большой степенью затененности

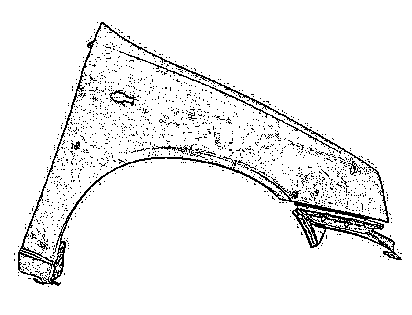
Рис. 11. Результат обработки затененного изображения

акцентироваться именно на границах образа, что и дало такое высокое качество выделения.

Из полученных результатов работы алгоритма можно сделать вывод, что алгоритм является чувствительным к наличию шума на исходном изображении, поэтому предварительно нужно выполнять корректирующие алгоритмы, например, медианную фильтрацию, что существенно снизит количество нежелательных артефактов. Анализируя исходные изображения и результаты, можно также заметить, что наилучший результат достигается для тех изображений, на которых объекты расположены на однотонном фоне, что позволяет алгоритму точнее определить пороговое значение для бинаризации. Дополнительной положительной стронной является то, что на работу алгоритма не влияет затененность, а в некоторых случаях она даже способствует получению лучшего результата. Несмотря на указанные незначительные недостатки, метод Adaptive Threshold является достаточно гибким инструментом для выделения контуров образов на цифровых изображениях и может довольно успешно применяться в системах автоматизации, робототехники и других отраслях, требующих идентификации объектов.