Использование метода диакоптики для анализа надежности программного обеспечения

Достаточно часто в качестве анализируемой выступает сложная система, состоящая из большого количества элементов, и анализ таких систем является непростой задачей. Практически все современные программы насчитывают сотни и даже тысячи отдельных функциональных модулей, каждый из которых является не менее сложной подсистемой. Таким образом, необходимы методы, которые бы позволили инженеру выполнять анализ системы по отдельным частям с возможностью объединения полученных результатов в одно аналитическое выражение, характеризующее всю систему. Тензорный метод, который дает возможность подобного преобразования с помощью специальных матриц, получил название метода диакоптики [1].

В случае анализа программы с использованием метода диакоптики применяются те же этапы анализа, что и при анализе обычной системы, но при этом появляется еще одна дополнительная особенность. Она заключается в том, что после получения аналитических соотношений всех подсистем необходимо сначала найти решения для всех данных уравнений и лишь затем все исходные подсистемы соединить в целую исходную систему.

Кроме того, если в состав системы уравнений, описывающих первоначальную систему, входило N отдельных уравнений с N неизвестными, то при разбиении системы на n отдельных подсистем для описания связей между ними вводятся к неизвестных. Поэтому необходимо найти ( N + к ) переменных в ( n + 1) независимых группах, а не просто решить систему из N уравнений с N переменными. Впрочем, такое усложнение дает значительное уменьшение габаритов исходных анализируемых подсистем.

Введение новых переменных требует построения и расчета отдельной цепи пересечений, в которой, как в определенном подпространстве, пересекаются друг с другом n подпространств. Вся эта цепь пересечений представляет собой некоторую миниатюрную копию исходной системы с намного меньшим числом переменных.

Однако с учетом роста производительности современных ЭВМ разбиение исходной системы на ряд подсистем может показаться неэффективным в связи с тем, что объем оперативной памяти современных машин исчисляется гигабайтами и анализ всей системы возможен сразу целиком. Этот анализ осуществляется достаточно просто, за исключением расчета обратных матриц. Объем вычислений для этой операции действительно велик и усложняется по нелинейному закону [2]. Поэтому целесообразно разбить исходную систему на ряд подсистем и рассчитать их раздельно, поскольку матрицы малых порядков намного проще преобразовать, и затем объединить результаты вычислений для получения аналитического описания всей системы.

В случае расчленения исходной системы на ряд подсистем может возникнуть предположение о том, что нужно не расчленять модель на ее графическом изображении, а просто определенным способом поделить матрицы. Однако это не соответствует действительности, так как разделение системы на подсистемы на рисунке сопровождается появлением новых, неизвестных сил связи, а деление матриц не приводит к появлению новых переменных, хотя возможность реализации этого на уровне матриц и существует, но на модели в виде изображения сделать это намного удобнее [3-5].

Из всех моделей наиболее приемлемы топологические модели, в которых каждая отдельная ветвь может быть индуктивностью, оператором, блок-схемой или другим элементом; и все элементы связаны между собой с помощью графа. А самой подходящий для представления и описания анализируемых величин является электротехническая терминология.

Описанный выше метод расчленения может быть использован несколькими способами:

• -    можно выделить один, два или более особо важных параметра в каждой из подсистем и произвести анализ всей системы с учетом именно этих параметров;

• -    можно найти собственные значения и собственные векторы каждой из подсистем и затем определить собственные значения и собственные векторы целой системы с меньшим объемом вычислений;

• -    можно оптимизировать некоторые характеристики или функции отдельных подсистем. Это позволяет затратить намного меньше времени на оптимизацию всей системы по сравнению с оптимизацией всей системы целиком.

Идея метода расчленения может быть использована для решения практически любых задач с большим числом переменных. При этом следует заметить, что результаты расчета каждой отдельной подсистемы, как правило, не являются целью данного метода, а используются как исходные данные для следующего шага - получения системы уравнений, описывающей поведение всей системы целиком. Расчет всех n подсистем завершается расчетом (n + 1)-й системы, которая является конденсированным вариантом полной системы. Кроме того, для метода расчленения характерно то, что любая проблема, которую приходилось решать при анализе исходной сис- темы, встретится и при анализе цепи пересечений, но решить ее в данном случае будет нетрудно с помощью более простых и быстрых аналитических методов.

Положительным моментом также является а то, что метод расчленений дает тот же самый результат, что и расчет всей системы целиком, но получить этот результат можно намного быстрее и проще. При этом если метод анализа отдельных подсистем будет достаточно точным, то и конечный результат будет таким же; если же методы будут приближенными, то и результат будет приближенным.

В тензорном методе [6] используется понятие элементарной ячейки - настолько малой части исходной системы, уравнения состояния которой устанавливаются сразу без дополнительных шагов анализа. Модель такой элементарной ячейки не может быть расчленена на более мелкие части. Для описания этой модели используется система n уравнений с n неизвестными [6; 7].

Все рассмотренные выше матрицы преобразования были неквадратными, а следовательно, не имели обратных матриц. Однако основная идея метода расчленения состоит в одновременном выполнении ряда преобразований с помощью матриц C и A и обратных им преобразований, причем только одно из этих преобразований будет либо расчленением, либо соединением. В тензорном анализе обычно используют такие матрицы преобразования, которые имеют обратные матрицы. Отсюда следует, что для реализации метода расчленения желательно использовать именно неособенные матрицы соединений. Однако для того чтобы перейти от неособенных и неквадратных матриц к квадратным, необходим иной подход. Именно такой подход реализуется в методе, названным диакоптикой.

Основная суть метода диакоптики состоит в следующем [7]:

Пусть имеется N элементарных ячеек, каждая из которых описывается отдельной матрицей параметров, причем каждая такая ячейка представляет собой черный ящик с некоторым числом полюсов (входов и выходов) и в дальнейшем не может быть разделена на части. Эти ячейки соединяются определенным образом и дают всевозможные сети, которые могут насчитывать произвольное число контуров, пар узлов и подсистем. Инвариантной величиной в данном случае остается лишь число реальных ячеек.

Если имеется система уравнений состояния, описывающая поведение системы для отдельно взятого случая, то тогда задача метода диакоптики состоит в получении уравнений состояния или решения для любой другой из указанных структур по уже известным уравнениям с помощью неособенной матрицы преобразования.

С практической точки зрения метод диакоптики сводится к следующему: в случае анализа сложной системы вместо нее можно рассчитать другую систему, которая затем может быть переведена в исходную систему с помощью уже упомянутых выше преобразований, причем анализ этой системы будет намного проще, чем исследование исходной системы. Иными словами, сначала нужно рассчитать ту систему, анализ которой не представляет особой трудности. Такой системой является группа не связанных подсистем. Каждая подсистема в данном случае рассчитывается независимо от других, а затем все полученные (n + 1) системы преобразуются с помощью матрицы C в решение исходной системы уравнений.

Обычно получают решения не для ортогональных, а для контурных или узловых цепей. Но и в этом случае возможен как переход к ортогональным цепям, так и обратный переход с введением дополнительных цепей.

Следует отметить, что переменные всех структур взаимосвязаны друг с другом. Для примера приведем связь переменных двух структур: A (рис. 1) и B (рис. 2). Для этого необходимо найти матрицу преобразований. Одна из рассматриваемых цепей содержит три контура, вторая - два контура. Поскольку при выборе контуров каждый из выбранных параметров должен циркулировать в замкнутом контуре, то для реализации этого процесса будут использоваться виртуальные блоки. Контуры выбираются произвольным образом.

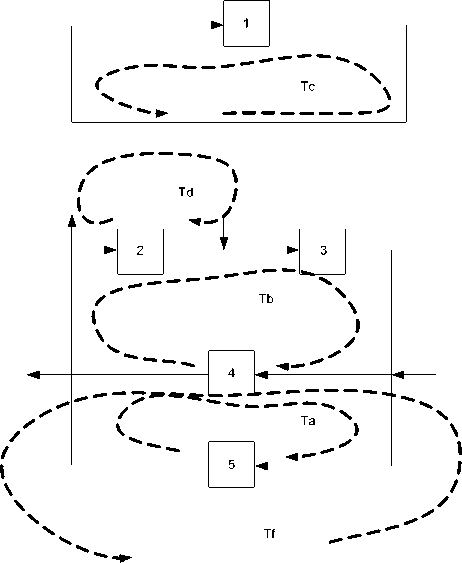
Рис. 1. Цепь А

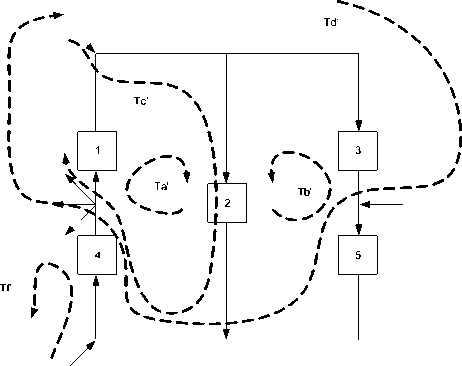
Рис. 2. Цепь В

По сле выбора контуров приравняем потоки, протекающие через одни и те же блоки. В итоге получится следующая система уравнений [8]:

Ta - Tb - Td - Tf — Ta ',

Tc — Ta ' + Tc ' + Td ' + Tf ',

Tb + Td — - Tb ' ,

• - Tb — Ta ' + Tb ' + Tc '.

Все эти уравнения можно получить путем преобразования токов соответствующей примитивной сети элементов, следовательно для сетей А и В примитивная сеть будет одинакова. Тогда

T^d — C E t a ,

Td — c be t B .

Для перехода от переменных примитивной сети к переменным сетей A и B следует приравнять оба полученных значения T^d .

Запишем эти равенства в матричной форме: c E t a — c Be t^B .

Теперь попробуем разделить обе матрицы на две части, одна из которых будет определять контуры, а вторая – пары узлов:

	"1 -1 0 -1 -1
	0	10	0
E A	1000		0
	0101		0
	0100		0
	"1	000	0
	1	011	1
C B —	0	10 -10
	0-	100	0
	1	110	0_

Ранее нами было получено соотношение, из которого следует, что ta — ( ce )-1 te — ( cb )-1 cbetB — cecbtb .

В то же время известно соотношение, которое позволяет перейти от одной сети к другой:

• t a — c A c E t b — c A t b .

EBB

Отсюда следует, что искомая матрица преобразования координат между двумя данными сетями определяется перемножением матриц:

A //""'E 4-1 /~^,e A^ pB CB ^{— (} CA ) CB ^— cecB "

Таким образом, матрица перехода между сетями имеет вид

	10 0 0 0
	10 111
C E — ( C B ) - 1 —	0 1 0 -10
	0 -10 0 0
	_1 1 1 0 0_

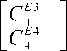
Произведя перемножение матриц CEA и CBE , полу- чим искомую матрицу перехода:

C A — C A ^x C E — ( C E ) ^{- 1 x} C E — BEBAB

	1	00	0 0		1	00	0 0
	1	01	11		1	01	11
—	0	10	-1 0		0	10	-10	—	A 1 CB _ C B 3
	0	-1 0	00		0	-1 0	00

A 2 C_B

A 4 C_B

1110 0     1110 0

В заключение найдем матрицу обратного перехода [9]:

	10 0 0 0
	10111
C AB — ( C B ) - 1 —	0 1 0 -10	—	A 1 B A 3 _ ^ B
	0 -10 0 0
	_1 1 1 0 0_

Итак, отметим, что метод диакоптики и тензорный анализ с использованием перехода от примитивного алгоритма к исходному основаны на едином аппарате тензорного преобразования координат между различными проекциями.

Помимо преимущества, связанного с сокращением размерности матриц, а следовательно, размерности решаемой системы уравнений, у метода диакоптики есть и другое, более ценное преимущество: решение для отдельных подсистем может быть получено и другими методами анализа – точными или приближенными [1–7]. В этом случае остается воспользоваться матрицей связности для получения решения всей системы. Кроме того, появляется возможность децентрализации процесса получения решения.

Возможна и другая ситуация, когда необходимо получить результаты для случая объединения нескольких программных модулей между собой. Структура и характеристики каждого из модулей и способ их соединения заданы, а характеристики всего алгоритма необходимо найти. И, наконец, каждый из элементов алгоритма в свою очередь может представлять собой не конечный элемент, а отдельный алгоритм.

Особенностью метода диакоптики является сочетание двух качественно различных методов анализа: методов, опирающихся в своих вычислениях преимущественно на аналитические решения систем уравнений без учета топологии системы, и методов, делающих основной упор на граф-схемы системы. И именно в методе диакоптики была впервые предпринята попытка объединения этих методов.