Использование метода функции размытия точки для анализа качества преобразования излучения при четырёхволновом взаимодействии на тепловой нелинейности (обзор)

При использовании четырехволновых преобразователей излучения, обращающих в реальном масштабе времени волновой фронт, в системах коррекции фазовых искажений необходимо знать, насколько точно пространственно-временная структура волны с обращенным волновым фронтом (ОВФ) соответствует пространственно-временной структуре, падающей на четырехволновой преобразователь волны. Знание такой связи позволяет определить как характерный минимальный размер неоднородностей искажающей среды, которые могут быть скомпенсированы при повторном прохождении волны с ОВФ через эту сред у, так и характерный минимальный временной масштаб изменения неоднородностей [1,2].

Вид этой свя зи существенным об разо м зависит от характеристик нелинейной среды, в кото -рой осуществля ется ч етырёхволново е взаимо -действие.

Одним из распространённых методов анализа кач еств а преобразования излуч ения при многоволновых взаимодействиях явля ется метод , осно -ванный на нахожд ении и анализе функции размытия точ ки (ФРТ). Этим методом, к настоящему моменту, достаточно подроб но изучена точ ность преобразования изображения при трехфотонных параметрич еских взаимодействиях как с понижением, так и с повышением часто ты [3-6], точ ность обращения во лнового ф ронта при четырёхволновом взаимодействии в средах с керровской нелинейно стью [7-9].

При этом практически отсутствуют работы, посвященные изуч ению качества об ращения волнового фронта при четырёхволновом взаи мод ей-ствии в средах с тепловым механизмом нелинейности [10-12]. До сих пор сред ы с теплово й нелинейно стью являются наиболее перспективными сред ами для обращения во лнового фронта излучения среднего ИК-д иап азо на длин волн . Тепло -вая нелинейность присутствует и оказывает существ енно е влияние при четырехволново м в заимо -действии и на друг и х типах нелинейно сти [13-15].

1. Вырожденное четырехволновое взаимодействие с плоскими волнами накачки [16]

Пусть в плоском слое с тепловой нелинейностью толщиной ℓ распространяются две волны накачки с комплексными амплитудами A ₁ и A ₂ , сигнальная волна с амплитудой A ₃ . В результате вырожденного четырехволнового взаимодействия ®+®-®=® генерируется объектная волна с амплитудой A ₄ (рис.1).

-нелинейная

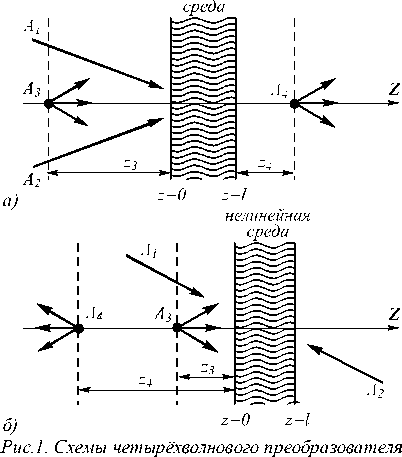
излучения с попутными волнами накачки (а); со встречными волнами накачки (б)

Стационарное волновое уравнение, описывающее такое взаимодействие, имеет вид

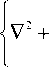
I 2 dn „ I

k2I 1 +---8 T I - 2 ik а

I n0dT )

II

•I E A j ⁺ к ■ с ■ I= °-⁽¹⁾ j )

Здесь n ₀ – среднее значение показателя преломления, k - волновое число, а - коэффициент поглощения, 8 T - изменение температуры, обусловленное выделением тепла при поглощении излучения.

Пространственное изменение температуры 8 T описывается уравнением Пуассона

V28 T +--8 q = 0,

^Л c p ^v

dA ₃( К , z ) . k I k dn _x . I

—3х-3—- +1—<--8 T,( z) -1 а) x dz        k3 z [ n 0 dT,

где Л - коэффициент температуропроводности, c_p - удельная теплоемкость, v - объемная плотность вещества. С учетом линейного по интенсивности поглощения излучения веществом

x A 3 ( к ₃, z ) = 0 dA 4 ( K 4 , z ) + i k

dz

k _{4 z}

k dn              I *

—— ^{8 T} 0 ^{( z} ) ^- i ^а ^ A 4 ^{( К} 4 , ^z ) = n 0 dT

8 q = а A A * .

Здесь а - коэффициент поглощения.

Будем рассматривать четырехволновое взаимодействие при след ующих предположениях: 1) справедливо приближение заданного поля по волнам накачки (| A ₁₂| >> | А ₃4| ) ; 2) коэффициент преобразования мал (| A 3| ² >> | A 4| ² ) ; 3) учитывается тепловая решетка, образованная при инт ерференции первой волны накачки с сигнальной волной (рассматривается случай, когда вторая волна нак ачки и сигнальная волна некогерентны).

Изменение температуры представим в виде суммы двух слагаемых:

. k2 dn ~ ,*     * * .= i--8T. (к = к, - к,, z) x

31 T 4      2

k 4 z n 0 dT

^X A 20 ⁽ z ^)exp { ^- i ^{( k} 2 z ^{- k} 4 z ) z } •

При анализе уравнений (6-8) не будем учитывать влияние изменения длины взаимодействия на амплитуды волн, распространяющихся в среде, т.е. k / k z = 1.

Уравнение Пуассона распадается на два уравнения

d ² 8 T ₀ dz ²

а+--

^Л c p ^v

( A 10 ⁽ z ) 4 *0 ⁽ z ) ⁺ A 20 ^{( z} ) ^A 2o ^{( z} ) ) = ⁰

, (9)

8 T = 8 T 0 + 8 T₃₁ + к . с.,

одно из которых 8 T 0 связано с распространением в среде волн накачки, а другое 8 T 31 - с интерференцией первой волны накачки с сигнальной волной.

Разложим составляющую изменения температуры 8 T ₃₁ по гармоническим решеткам

tx>

8 T ₃₁( r ) = J 8 T ₃₁( k _t , z )exp( - i к _T р ) d к _T .

—^

Здесь 8 T 31 - амплитуда спектра тепловой решет-

ки, р ( x , у )

*          *

вектора r , к T

поперечная составляющая радиус

—*      —*       —* —*

= К 1 - К 3 = К 4

к ₂ - пространствен-

ный вектор гармонической решетки.

Пусть волны накачки являются плоскими волнами

A j⁽ r ) = A j0 ⁽ z ) exp { - i ^— j ^{P -} ik jz z } ,

j = 1,2 .(5)

Сигнальную и объектную волны разложим по плоским волнам

^

A 3,4 ^{( —} ) = J ^ A 3,4 ^{( K} 3,4 , z ^)exp { ^- i ^K 3,4 ^{р - ik} 3,4 z z } ^{d K} 3,4 •

-^

Здесь кj и kjz - поперечная и продольная со ставляющие волнового вектора kj .

Учитывая сделанные выше предположения, в приближении медленно меняющихся амплитуд волновое уравнение (1) распадается на четыре уравнения вида

—^{j 0} + i— —8 T _o - i а| A -_o = 0, j = 1,2, (6)

0              j 0

dz     k jz [ n 0 dT

d ² dz ²

-К:

:T 18 T 31 ( k _T , z ) =

а         *

-----A 10 ⁽ z ) A 3 ^{( K} 3 , z ) exp { ^- i ^{( k} 1 z ^{- k} 3 z ) ^z } .

^Л C p ^v

В предположении, что распространение волн не меняет темп ературу на передней и задней гранях нелинейной среды

8 T ( z = 0) = 8 T ( z = I ) = 0, с учетом граничных условий

A io ( z = 0) = A ",

A3(K3, z = 0) = A30(63), получим решения уравнений (6)-(7) A10(z) = A100 exp {-аz - iC(z)} , A3 (к3, z) = ^30(63) exp{-аz - iC(z.

где C ⁽ z ) = —dn- j⁸ T 0 ⁽ z 1 ) dz 1 .

n ₀ dT ₀

С учетом изменения вдоль оси Z амплитуд волн накачки и сигнальной волны уравнение (10) имеет решение вида

8 T ₃₁( k _T , z ) =

fA 1 ⁰ 0 A 30

в ² -K T.

x

x

₂ sh^ , I { ^exp^{( -}K T ^z ) [ e^xp⁽ K T ^{l ) - e}xp^{( -e i )} ] } ⁺

⁺ 9 1 e { ^exp^{( K} i^z ) [ ^exp^{( -e i ) - e}xp^{( -K} t ^{l )} ] } 2 s h К t I

^{- e}xp^{( -e z} ) } •

-

Здесь f = аЛ c_p v , к _T = | к _T |, в = 2 а + i ( k 1 _z

^{- k} 3 z ) •

Если четырёхволновое взаимодействие осущ ест-вляется в схеме с попутной геометрией и вторая волна накачки - плоская ( A 2 = A 20 ( z )exp { - ik₂ r } ) , то

нейности в центре поля зрения ( р ₀ = 0) в параксиальном приближении примет вид

составляющая температуры 5 T ₀ имеет вид

м

G ( р , z з , z 4 ) = fA 10 A20^^-^

-L P ^-к t

X

⁵ T = ^ aXvc. { I ' Н • ' * 1⁺

+ I ₂ exp ( - 2 al ) [ exp ( 2 a z ) - 1 ] +                 (15)

⁺ z ^{[ 1 -} exP ( 2 ^a z ) 1 ( I 1 ^- I 2 ) ,

[ 1     [ exp ( -pl ) - exp ( к _T l ) [

[ 2 sh к _T l        [ к _T + ip ]

x [exp ( к _T l - ip l ) - 1] +

1    [ exp ( -pl ) - exp ( -к _T l ) 1

2 sh к _T l         [ к _T - ip ]

где I j = ( A 0o ) 2 , A 200 = A 2o ( z = l ).

С учётом выражения (14) связь между амплитудой пространственного спектра объектной и амплитудой пространственного спектра сигнальной волны на задней грани нелинейного слоя в схеме с попутными волнами накачки (рис.1а) A ₄( к ₄, z = l ) с точностью до постоянного множителя имеет вид

[ exp ( - 2 al ) - 1 1

x [exp ( -к _T l - ip l ) - 1] +  -----2--------x

x exp

■ к 2

i 4 z 2 k ⁴

. к2

i 3 z 2 k ³

^- i ^к 4 ^р

d к ₄,

—w

A 4 ( 6 4 , z = l ) =

f4 o A Oo A ;o ( K 3 )

P 2 -к T

X

[ 1     [ exp ( -pi ) - exp ( к _T l ) [

[ 2 sh к _T l        [ к _T + ip ]

x [exp ( к _T l - ip l ) - 1] +

где к ₃ = к 1 +к ₂ -к ₄. Выражение (17) полностью описывает качество ОВФ четырехволновым преобразователем излучения. На рис.2 приведен характерный график зависимости нормированного на максимальное ( G _max ) значение модуля ФРТ ( G = | G/ G _max |) от поперечной координаты.

+--

2 sh к _T l

[ exp ( -pi ) - exp ( -к _T l ) 1

[ ^к T ^-

x [exp ( -к _Т I - ip I ) - 1] +

iP ]

^[ exp ( 2 « ^l ) ^- 1 1 2 a

.

Здесь p = ( k _{4 z} - k _{2 z} ) .

В схеме со встречными волнами накачки (рис.1б) выражение, связывающее амплитуду пространственного спектра объектной волны A ₄( к ₄, z = 0) с амплитудой пространственного спектра сигнальной волны на передней грани нелинейного слоя, совпадает с выражением (16) при замене параметра p на - p .

Пусть сигнальная волна распространяется от точечного источника, расположенного на расстоянии z ₃ от передней грани нелинейного слоя (плоскость фокусировки сигнальной волны): A ₃( р , z 3 ) = 5 ( р-р ₀). Будем рассматривать поле объектной волны на расстоянии z ₄ от задней грани нелинейного слоя (плоскость фокусировки объектной волны) в схеме с попутными волнами накачки, на расстоянии z ₄ от передней грани нелинейного слоя в схеме со встречными волнами накачки.

ФРТ характеризует отклик линейной оптической системы на точечный сигнал. С учетом (16) выражение для ф ункции размытия точки четырехволнового преобразователя излучения, на тепловой нели-

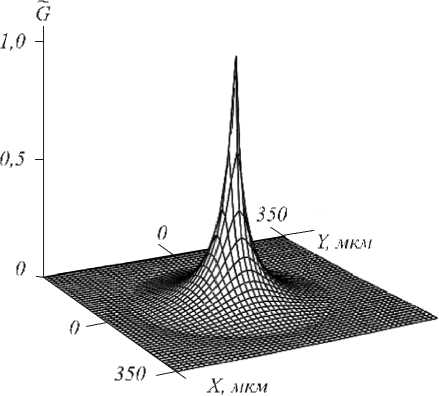
Рис.2. Зависимость модуля ФРТ четырёхволнового преобразователя излучения на тепловой нелинейности с учётом одной тепловой решётки от поперечных координат

Численный анализ выражения ф ункции размытия точки проводился для излучения CO ₂ – лазера (λ=10,6 мкм). В качестве нелинейной среды использовался сероуглерод (n 0 =1,6, а =1 см^-1).

Количественной мерой качества ОВФ может служить ширина модуля ФРТ.

Направление координатных осей Х и Y выберем таким образом, чтобы ось Х лежала в плоскости волнового вектора первой волны накачки и точечного источника сигнальной волны, а ось Y была направлена перпендикулярно этой плоскости. Введем понятие ширины модуля ФРТ в направлении осей X

и Y ( А х = | x 1 - x 2| , A у = | у 1 - у ₂| ), где x 1,2 и у₁₂ определяются из условий

| G ( X = Л ^, у = 0)| = 1 G max ,                    (18)

| G ( X = 0, у = У 1,2 )| = 1 G max .                       (19)

Расчеты показывают, что при фиксированном положении плоскости фокусировки сигнальной волны существует оптимальное положение плоскости фокусировки объектной волны (плоскость оптимальной фокусировки), в пределах которой ширина модуля ФРТ минимальна. Положения плоскостей оптимальной фокусировки объектной волны при рассмотрении ширины модуля ФРТ в направлениях, задаваемых осями X ( z 4 opt // ) и Y ( z 4 opt _±) , различны.

На рис.3 приведены характерные графики зависимости ширины модуля ФРТ в направлении оси X в плоскостях оптимальной фокусировки от направления распространения волн нак ачки как в схеме с попутны ми (кривая 2), так и в схеме со встречными (кривая 1) волнами накачки. Считалось, что волновой вектор второй волны накачки расположен в плоскости XZ.

Ширина мод уля ФРТ четырехволнового преобразователя излучения на тепловой нелинейности с ростом толщины нелинейного слоя увеличивается быстрее в схеме с попутными волнами накачки, чем в схеме со встречными волнами накачки (рис.4).

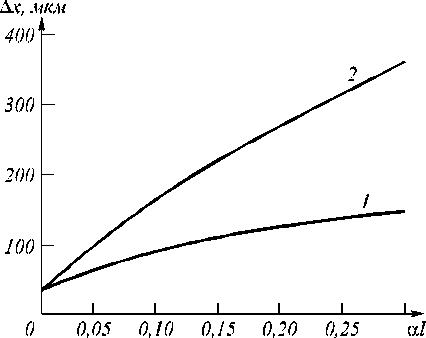
Рис.4. Зависимость ширины модуля ФРТ от толщины нелинейного слоя: 1) схема со встречными волнами накачки, К 1 / k = к ₂ / k = 0 ; 2) схема с попутными волнами накачки, к ₁ / k = -к ₂ / k = 0, 017 рад

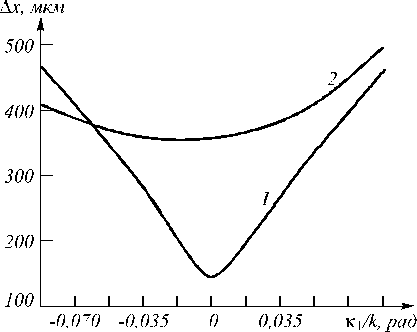
Рис.3. Зависимость ширины модуля ФРТ от направления распространения первой волны накачки при af = 0,3 :

1) схема со встречными волнами накачки, к ₂ / k = 0 рад ;

2) схема с попутными волнами накачки, к ₂ / k = - 0,017 рад

Как следует из выражения (17), при z ₃ ^ 0 по сравнению с z ₃ = 0 поворот волн накачки приводит к смещению ФРТ в поперечном направлении на величину ( к 1 + к ₂ ) z ₃ / k , возникает постоянный фазовый набег равный ( к 1 + к 2 ) 2 z ₃/ k . Смещение положения максимума модуля ФРТ относительно положения исходной точки ( aZ ) , как и для четырехволнового преобразователя в среде с керровской нелинейностью [20], хорошо описывается выражением

—*

AZ =

( ^к 1 ^+к 2 ) k

z ₃

f

⁺ 2 ^ 0

В схеме со встречными волнами накачки, распространяющимися строго вдоль оси Z, положение плоскости оптимальной фокусировки совпадает с положением плоскости фокусировки сигнальной волны.

Минимальное значение ширины модуля ФРТ наблюдается при совпадении направлений распространения волн накачки в схеме с попутными волнами накачки и при распространении строго навстречу друг друг у волн накачки в схеме со встречными волнами накачки. По мере отклонения направления распространения первой волны накачки от направления распространения второй волны наблюдается монотонное увеличение ширины модуля ФРТ. Скорость изменения ширины модуля ФРТ по мере отклонения направления распространения первой волны накачки от направления распространения второй волны в схеме со встречными волнами накачки выше, чем в схеме с попутными волнам накачки.

2. Четырехволновое взаимодействие в схеме с попутными волнами накачки, при учете двух тепловых решеток [17,18]

Наряду с тепловой решеткой, образованной при интерференции первой волны накачки и сигнальной волны, существенную роль в характеристике четырехволнового преобразователя излучения может сыграть учет еще одной тепловой решетки , возникающей при интерференции второй волны накачки и сигнальной волны. Особенно это важно при рассмотрении четырехволнового взаимодействия в схеме с попутными волнами накачки (рис.1а) при условии, что как сигнальная, так и волны накачки – это волны от одного и того же источника излучения.

В этом случае изменение температуры представим в виде суммы трёх слагаемых:

8 Т = 8 Т 0 + 8 Т 31 +8 Т ₃₂ + к . с .                   (20)

Учитывая наличие в нелинейной среде двух тепловых решеток, представим объектную волну в виде суммы двух волн A 4 = A 41 + A 42 , каждую из которых

также разложим по плоским волнам

—

A 4j⁽ r) = J А Д 4j , z )exP { " i ^K 4 j P ^- ik 4jz z } d ^K 4j , ^j = 1,2.

——

Проводя рассуждения, аналогичные рассуждениям, приведенным при наличии одной тепловой решетки, получим с точностью до постоянного множителя выражения для пространственных спектров амплитуд объектной волны на задней грани нелинейного слоя

качки). В качестве нелинейной среды возьмем ацетон ( a = 40 см ^{— 1}, n ₀ = 1,36 ).

На рис.5 приведен характерный график зависимости от поперечных координат нормированного на максимальное значение модуля фун кции размытия точки, полученный методом численного анализа выражения (22).

A ( к -К -к _z-Л- fA i⁰0 A 00 A ^з) _x 4 4/^ = ^ ^K 3 , z = ^{l )} = ^ 2 _—K 2 ^X

[ i    Гexp(—Pl)—exp(кTl)l x 1-------~------г-------5"

^ 2 sh к _Tj l        Г к _Tj + ip J

x[exp (к Tj l — ipj l) — 1] +

1     F ^eXP ( ^— P ^l ) ^— e^XP ( ^—K Tj ^l ) J

• + ~ ,    7 гй

• ² sh ^к j       Г К Tj — iP j J

Г exp ( — 2 al ) — 1 J )

• x[exp(—кTjl — iPjl^ — 1] +  -----—

где        в= 2a + i(kjZ -kзz),        кT =|к-—кз| , p1 = (k2z — k41 z), P2 = (k 1 z — k42z). В параксиальном приближении при условии, что волны накачки падают на нелинейную сред у под одинаковыми углами (к 1 = —к2): pj = (к2j — к2) /2k .

C учетом (14) получим с точностью до постоянного множителя выражение для ф ункции размытия точки четырехволнового преобразователя излучения на тепловой нелинейности в схеме с попутными волнами накачки в центре поля зрения в виде

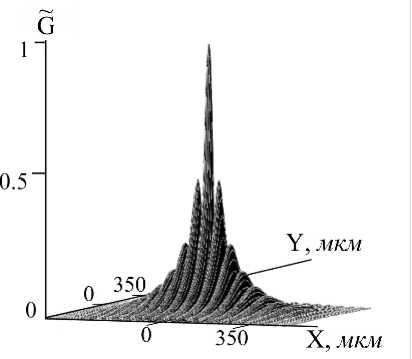
Рис.5. Вид модуля функции размытия точки, угол между волнами накачки 6° и al = 1,44

- 2

G p ( p , z з , z 4 ) = J^

1    ^[exp ( ^— P^l ) ^— exp ( ^к Tj ^l ) J

—=

- - j = 1

2 sh к Tj l

[ к T + ip J

x

x [exp ( к Tj l — ip j l ) — 1] +

1     [ exp ( ^— P^l ) ^— exp ( ^—к Tj ^l ) J

2 sh к _Tj l

[ ^к Tj- i^p j J

x

x [exp ( —к _Tj l — ip j l ) — 1] + [ exp^{(—2a l ) — 1}J )

⁺         I              f ^x

2 a

к 4 .

^{x exp} i^k z

^^^^^^

. к 2

i ³ z 2 k ³

^^^^^^

—к

——

——

i к 4 j p d к 4

4 j .

Будем считать, что волновые вектора волн накачки лежат в плоскости XZ (плоскость волн на-

Из-за интерференции двух объектных волн A ₄₁ , A ₄₂ , генерируемых в нелинейной среде, вид модуля функции размытия точки в плоскости волн накачки имеет периодическую структуру с выраженным центральным максимумом. С увеличением угла между волнами накачки увеличивается число максимумов. Расстояние между максимумами и их ширина, в том числе и ширина центрального максимума, уменьшаются.

Численный анализ выражения (22) показывает, что при малых уг лах падения волн накачки на нелинейную среду к j Ik <<  1 и al <  1 положение плоскостей z _{4 opt ±} и z _{4 opt} // совпадает и определяется выражением вида

l z4 opt ± = z4 opt // = z 3 + . (23) n0

При фиксированном направлении распространения одной из плоских волн накачки, например, первой ( к ₁ = const ) изменение направления распространения второй волны нак ачки приводит к изменению ширины мод уля ФРТ в плоскостях оптимальной фокусировки, изменению положений плоскостей оптимальной фокусировки. При увеличении угла межд у волнами накачки наблюдается резкое уменьшение ширины модуля ФРТ в плоскости волн накачки (кривые 1,2 на рис.6) и незначительное уменьшение ширины мод уля ФРТ в плоскости перпендикулярной плоскости волн накачки (кривые 3,4 на рис.6). При этом увеличивается и расстояние межд у плоскостями оптимальной фокусировки z 4 opt // и z 4 opt _± .

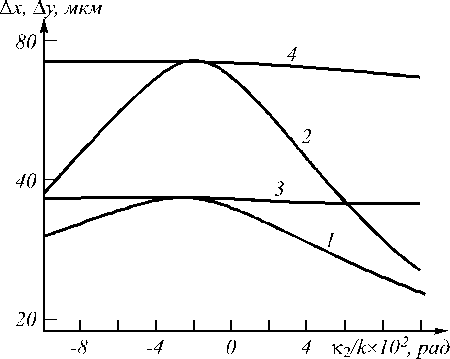
Рис.6. Зависимость ширины модуля ФРТ от угла, под которым распространяется вторая волна накачки: кривые 1,2 в плоскости волн накачки; кривые 3,4 в плоскости перпендикулярной волнам накачки; κ1/k=0,017 рад; ℓ=400 мкм (2,4), 200 мкм (1,3)

Зависимость ширины модуля ФРТ в плоскости волн накачки от угла межд у волнами накачки при | к 1 21 / k <<  1 хорошо описывается параболической функцией

Л х = Л х о { 1 - k 2 [ K i -к 2 ] 2 ,                   (24)

где Л х ₀ - ширина модуля ФРТ при совпадении направления распространения волн накачки ( к 1 = к ₂), к j = | к j |, ц - параметр, характеризующий скорость изменения ширины модуля ФРТ в зависимости от угла межд у волнами накачки, возрастающий с увеличением толщины нелинейного слоя. При I = 400 мкм параметр ц = 179 .

С физической точки зрения, сужение модуля ФРТ в плоскости волн накачки аналогично уменьшению ширины пятна при дифракции Фраунгофера на двух отверстиях с ростом расстояния между отверстиями.

Увеличение толщины нелинейного слоя приводит к относительному сдвиг у положения плоскостей оптимальной фокусировки к нелинейному слою. При этом ширина модуля ФРТ в плоскостях оптимальной фокусировки z 4 opt // и z 4 opt _± изменяется по закону прямо пропорциональному толщине нелинейного слоя в степени одна вторая

Лх = Р 1 JI , Л y = р ₂ V7 .                      (25)

Здесь р j - коэффициенты, в 1 < в ₂. Величина коэффициента в 1 уменьшается с увеличением угла межд у волнами накачки.

• 3.    Квазивырожденное четырехволновое взаимодействие [19]

• 3.1. Схема со встречными волнами накачки

Интерес к квазивырожденному четырехволновому взаимодействию ц + ®2 - ц = ®2 обусловлен возможностью наряду с получением волны с обра- щенным волновым фронтом одновременно осущ е-ствлять перевод излучения с одной частоты на другую, что оказывается предпочтительно при решении целого ряда задач. Первая волна накачки и сигнальная волна имеют частоты равные ц, а частоты объектной волны и второй волны накачки равны ц.

В схеме со встречными волнами накачки выражение для амплитуды пространственного спектра объектной волны на передней грани нелинейного слоя совпадает с выражением (16) при условии, что ( k 1 - k 3 ) z = ( к 3 - к 2 ) / 2 k 1 , p = ( к 4 - к 2 ) / 2 k ₂ в схеме с попутными волнами накачки, p = - ( к 2 - к 2 ) / 2 k ₂ в схеме со встречными волнами накачки, k 1 = ц п ₀₁ / c , k ₂ = ® ₂ п ₀₂ / c , п ₀₁ и п ₀₂ - значения показателя преломления на частотах ц и ® ₂.

Численный анализ выражения для ФРТ квазивы-рожденного четырехволнового преобразователя излучения проводился для излучения CO ₂ лазера ( Х = 10,6 мкм ) , которое записывает тепловую решётку и He - Ne лазера ( Х 1 = 0,63 мкм ) , который генерировал вторую волну накачки. В качестве нелинейной среды использовался слой ацетона.

Пусть волны накачки распространяются вдоль оси Z строго навстречу друг другу. В этом случае ФРТ зависит от модуля поперечной координаты. На рис.7 (кривая 1) приведен график зависимостей ширины мод уля ФРТ в плоскости оптимальной фокусировки ( Лр ) от отношения частот волн накачки.

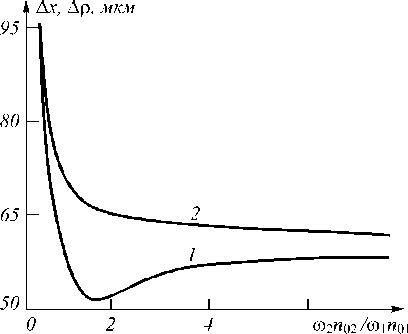
Рис. 7. Зависимость ширины модуля ФРТ от отношения частот волн накачки: 1) схема со встречными волнами накачки, к1 / k = к2 / k = 0 ; 2) схема с попутными волнами накачки, к1 / k = -к2 / k = 0,017рад ;

а 1 1 = 1,6 ; k 1 l = 322

Ширина мод уля ФРТ в плоскости оптимальной фокусировки минимальна при вырожденном четырехволновом взаимодействии. По мере отклонения частоты второй волны накачки от частоты волн, записывающих тепловую решетку, ширина мод уля ФРТ монотонно возрастает.

При фиксированных параметрах волн накачки ув еличение толщины нелинейного слоя приводит к монотонному росту ширины мод уля ФРТ (рис.8. кривая 1). Если нелинейная среда «тонкая» ( a l <  1 ) , то, как и для вырожденного четырехволнового пре-

образователя излучения, ширина модуля ФРТ прямо

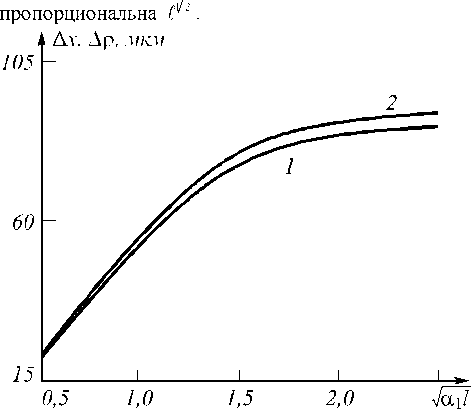
Рис.8. Зависимость ширины модуля ФРТ от толщины нелинейного слоя: 1) схема со встречными волнами

Пусть вторая волна накачки является плоской, а амплитуд а первой волны накачки меняется по гауссову закону

. (-X Г 1 k 1 ² I ₂ Г 1 к 1 I ⁴< r ) = [ 7 ^{+ 1} r J exp ^p [ 7⁺' r J ^— ikz ,(26)

A ₂ ( r ) = exp { ikz } .

Здесь 2 a – диаметр волны накачки, R – радиус кривизны волнового фронта. Выражение (26) может быть использовано для оценки влияния на вид ФРТ самовоздействия гауссовой волны накачки, приводящего к изменению кривизны волнового фронта.

При учете пространственной структуры волн накачки ФРТ четырехволнового преобразователя излучения есть когерентная сумма ф ункций размытия точки ( G ( p , z 3 , z 4 , к 1 , к 2 )), соответствующих плоским волнам накачки

^

G , ( p , z 3 , z 4 ) = j G ( p , z 3 , z 4 , к J , к 2 ) d к 1 d к 2 .      (27)

—^

накачки; 2) схема с попутными волнами накачки; k2/k1=17

3.2. Схема с попутными волнами накачки

Пусть при распространении волн накачки выполняется условие к 1 + к 2 = 0. В этой схеме изменение ФРТ четырехволнового преобразователя излучения зависит как от координаты x , так и от координаты y .

На рис.7 (кривая 2) для плоскости перпендикулярной плоскости волн накачки приведен график зависимости ширины модуля ФРТ в плоскости оптимальной фокусировки от отношения частот волн накачки. В плоскости волн накачки значение ширины модуля ФРТ отличается от значения в плоскости перпендикулярной плоскости волн нак ачки менее чем на 1%. С увеличением частоты второй волны накачки ширина мод уля ФРТ в плоскости оптимальной фокусировки, монотонно убывая, выходит на постоянное значение.

Как и в схеме со встречными волнами накачки, ув елич ение толщины нелинейного слоя приводит к ро сту ширины мод уля ФРТ (рис.8. крив ая 2). При этом зависимости А х и А у от толщины нелинейного слоя с точностью 0,1% при к 2 /к 1 = 17 совпад ают.

4. Влияние пространственной структуры волн накачки [16,17]

4.1. Одна тепловая решетка

Рассмотрим вырожденное четырехволновое взаимодействие в схеме со встречными волнами накачки при условии записи в нелинейной среде тепловой решетки 8 T 31 .

С учетом (17), (26) выражение для ФРТ с точностью до постоянного множителя примет вид ~ 00

G, (p,z3,z4) = J J ----Г X в — кт

—^ —^         I

_x I 1    Г ^еХР ( ^— И ^{— ex}P ( ^к t ^l ) J

[ 2 sh к _T l          [ к _T + ip ]

[exp ( к _T l — ip l ) — 1] +

₊    1   [exp^ —P£ ) 2 ^ex^p(2 ^к г ^l ) ]

2 sh к _T l         [ к _T — ip ]

—

x

[ exp ( — 2 al ) — 1 1 )

x [exp ( —к _T l — ip l ) — 1] +  ----- 2------- ^J x

x exp

x exp

к 2 Г 1 . к

4 a ²⁺ⁱ 2 R

■ к 2

i 4 z 2 k ⁴

—

■ к2

i 3 z 2 k ³

. —— —-

^— i ^к 4 P

d к 1 d к ₄.

На рис.9 (а, б) сплошными линиями приведены характерные графики зависимости ширины мод уля ФРТ от радиуса волны накачки, кривизны волнового фронта, полученные при численном ан ализе выражения (28). В качестве нелинейной среды рассматривался сероуглерод ( a = 1 см ^{— 1}, n ₀ = 1,6).

Уменьшение радиуса волны накачки, увеличение кривизны ее волнового фронта приводит к увеличению расходимости волны накачки и, как следствие, к увеличению ширины мод уля ФРТ четырёхволнового преобразователя. По мере удаления плоскости фокусировки объектной волны от передней грани нелинейного слоя скорость изменения ширины модуля ФРТ с увеличением расходимости волны накачки возрастает .

Для качественного анализа в лияния пространственной структуры волны накачки на качество ОВФ заменим ФРТ четырехволнового преобразователя излучения с плоскими волнами накачки в плоскости оптимальной фокусировки гауссовой функцией

G 1 ^{( p} , z з , к i ) = -1exp L b o         I

1 (

b2 I

- К ( I p— I z 3 +-- к (    2 n 0

+

I G s i ( p , z з)|

. к2 (      i

+ i ¹ z ₃ +

2 к ( ³ 2 n 0

= exp <

^^^^^^^

p ²

tn

.

Здесь b ₀ – параметр, характеризующий ширину модуля ФРТ в случае плоских волн накачки, распространяющихся строго навстреч у друг друг у. При записи выражения (29) учитывали, что для плоских волн накачки при совпадении плоскостей фокусировки сигнальной и объектной волн ( z ₃ = z 4 ) поворот первой волны накачки на угол |к J / к приводит к смещению изображения в поперечном направле-

। K1l ( нии на величину J—Ч z3 +--I, возникает постоян-к I    2 n о J к2 ( ный набег фазы равный -1 z3 +

2 к (     2 n ₀ J

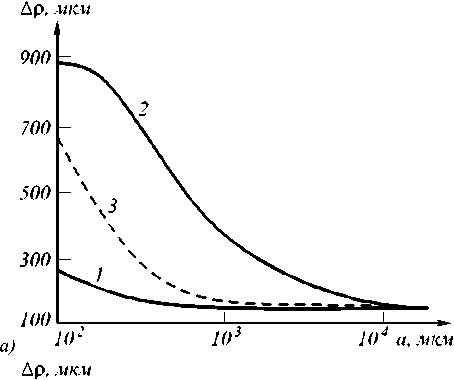
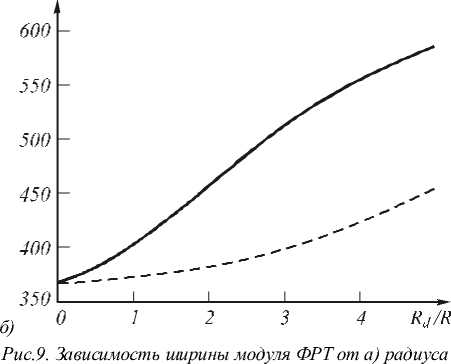
первой волны накачки, αℓ=0,3, z3/ℓ=0 (1), 7 (2,3); б) кривизны волнового фронта волны накачки, αℓ=0,3, z3/ℓ=7

Подставив (29) в (27), получим приближенное выражение для ФРТ. Модуль приближенного выражения для ФРТ c точностью до постоянного множителя имеет вид

b 0 ²

1—

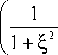
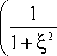
A ²

+ tn I +

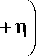
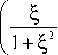
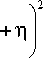
ka2        kb2       R где Rd =— , Rg = ^, ^ = "d , 2        2R

n=

z 3 + 1/ 2 n ₀

R d

t =

z 3 + 1/ 2 n ₀

R ,

g

Используя (30), найдём приближённые выражения для ширины мод уля ФРТ в двух предельных случаях: 1) опорная волна с плоским волновым фронтом (R=∞), 2) опорная волна от точечного источника ( а =0)

Ap ₁ = 2 Ь ₀л/1П2

Ap ₂ = 2 b ₀Vln2

X

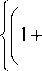
1 z 3 + 1) 2 n ₀ J

1 — t n(1 + n) (1 +1n)2 +n2

1 +

R z 3 +1/ 2 n 0

+ 1 ² r

x

Из в ыражения (32) след ует, что максимально е ув елич ение ширины мод уля ФРТ при изменении кривизны волнового ф ронта волны накачки на-блюд ается при расположении точ ечного источника опо рно й во лны на передней грани нелинейного слоя

Ap 2 ( R = 0) = { 1 + 1 ² } ¹² Ap 2 ( R =~ ). (33)

Штриховыми линиями на рис.9 изображены графики зависимости ширины модуля ФРТ, полученные с использованием выражения (30). Наблюдается качественное соответствие зависимостей ширины модуля ФРТ, полученных как с использованием точного, так и приближенного выражений для ФРТ. Отличие значений ширины мод уля ФРТ, полученных с использованием точного и приближенного выражений, по-видимому, связано с наличием у ФРТ, рассчитанной по формуле (17), широких «хвостов», которые не учитываются при аппроксимации функц ии размытия точки гауссовой функцией.

4.2. Две тепловые решетки

Рассмотрим вырожденное четырехволновое взаимодействие в схеме с попутными волнами накачки при условии записи в нелинейной среде тепловых решеток 8 T₃₁ и 8 T ₃₂.

Пусть одна из волн накачки, например, вторая является плоской, а пространственный спектр амплитуды первой волны накачки меняется по гауссову закону

••V

A ₁( κ ₁, z = 0) = exp

a 2 ( К 1 -К _w)²

G 2 ( x ) =

4π

8 πµ x ² + a ² a ₀ ²

×

А2(К2,z = 0) = 8(К2 -К20).

Подставив в (27) выражение для ФРТ при условии плоских волн накачки (22) с учетом (34), получим выражение для ф ункции размытия точки четырехволнового преобразователя излучения на тепловой нелинейности с попутными волнами накачки,

I X                       2

^x exp 1--2 ^- ( ^К 10 ^-К 20 )

I a 0

а ² |, 8 ц х ²

+ 1+

^ а а 0

. (37)

которое в центре поля зрения с точностью до посто-

янного множителя имеет вид

∞∞ 2

G . 2 = HS

-∞ -∞ j ⁼ 1

1     ^[ exp ( ^{-в 1} ) ^- exp ( ^К t? ¹ ) ]

2 sh к Tjl        [ к Tj + ip ]

×

x [exp ( к _Tj l - ip ? I ) - 1] +

1     ^{[ ex}P ( ^{-e i} ) ^{- ex}P ( ^-К t /)1

+×

2 sh к _Tj 1          [к _Tj - ip ? I

x[exp (-КTjl - ip?I) -1] +

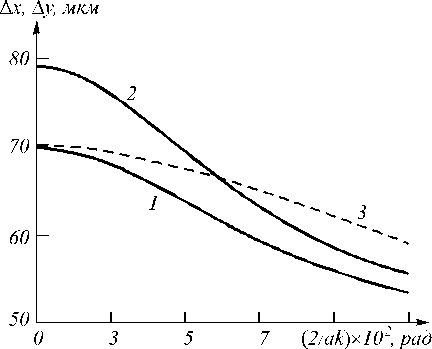
Рис.10. Зависимость ширины модуля ФРТ в плоскости волн накачки (1,3), в плоскости перпендикулярной волнам накачки (2) от расходимости второй волны накачки;

К ₁₀ = -К ₂₀ ; K 10 /k=0,017рад.; 1=400 мкм

[exp (-2al)-1]2α

- exp

κ24j i 2k z4

К2_

- i ³ z ₃ - i κ _{4 j} ρ 2 k

2 ^    ^ 2

I a (к, - к ) I „ „ x exp 1-- ^-4— 1⁰²- - d k _{4 j}d К 1 .

×

Заметим, что при выводе выражений (28), (35) не учитывалось изменение температуры ( δ T 0 ) вследствие распространения в нелинейной среде волн накачки.

В качестве нелинейной среды рассматривался ацетон ( α = 40 см ^{- 1} , n ₀ = 1,36 ).

Численный анализ выражения (35) показывает, что увеличение расходимости волны накачки при-

водит к монотонному уменьшению ширины мод уля ФРТ. Такая зависимость перестаёт выполняться, начиная с определённого значения расходимости, при

На рис.10 (кривая 3) приведена зависимость ширины мод уля ФРТ от расходимости волны накачки, рассчитанная с использованием выражения (37). Наблюдается качественное согласие полученны х зависимостей как с использованием точного, так и приближенного выражений для ФРТ. Однако с увеличением расходимости волны накачки отличие межд у точным и приближенным значениями ширины модуля ФРТ возрастает, что связано, по-видимому, с нарушением параболической зависимости ширины модуля ФРТ в случае плоских волн накачки с ростом угла межд у волнами накачки.

котором величина центрального максимума мод уля ФРТ становится меньше, чем удвоенная величина соседних максимумов. С увеличением расходимости сближаются значения ширины мод уля ФРТ в плос- кости волн накачки и в плоскости перпендикулярной волнам накачки (рис. 10. кривые 1,2).

Для качественного анализа влияния расходимости волны накачки на вид ФРТ в плоскости волн накачки заменим ФРТ черырехволнового преобразователя с плоскими волнами накачки гауссовой функцией

G '( x , ^К 1 , ^К 2 ) =      exp I^-          "           2

^{A x 0}      J а О ^{[ 1 -}ц ( ^К 1 ^-К 2 ) ]

где a ₀ = 0,6 ∆ x ₀ . При записи выражения (36) учитывали изменени е ширины модуля ФРТ в зависимости от угла межд у плоскими волнами нак ачки по параболическому закону (24).

Подставив (36) в (27) и проинтегрировав по d К 1 и d К ₂, получим приближенное выражения для ФРТ в виде

Заключение

Проведем сравнение полученных в работе численных результатов ширины модуля ФРТ, определяющей разрешение четырехволнового преобразователя излучения, с имеющимися экспериментальными результатами.

В работе [11] представлены результаты эксперимента по восстановлению волнового фронта при вырожденном четырёхволновом взаимодействии на тепловой нелинейности. Запись тепловой решётки осуществлялась излучением CO2-лазера в схеме со встречными волнами накачки, в качестве нелинейной среды использовался CCℓ4. Удалось скомпенсировать искажения, внесённые в сигнальную волну фазовой пластинкой с характерным размером неоднородностей около 400 мкм. Таким образом, экспериментально полученное разрешение четырёхволнового преобразователя излучения составило не менее 400 мкм. К сожалению, в работе не уточняется толщина нелинейного слоя и положение плоскости фокусировки объектной волны, которые использовались в эксперименте по компенсации фазовых искажений. Авторы осуществ- ляли четырехволновое взаимодействие в нелинейной среде, толщина которой менялась от 100 мкм до 5 мм.

Ширина модуля ФРТ, рассчитанная с использованием выражения (17), в области оптимальной фокусировки при толщине слоя четыреххлористого углерода ℓ=600 мкм (именно при такой толщине в работе [12] коэффициент отражения достигал максимального значения) составляет 80 мкм. При увеличении толщины нелинейной среды до 3 мм ширина модуля ФРТ в области оптимальной фокусировки увеличилась до 130 мкм, отстройка области фокусировки объектной волны от области оптимальной фокусировки на 6 мм приводит к увеличению ширины модуля ФРТ до 440 мкм.

В работе [12] экспериментально исследовалось преобразование изображения при квазивырожден-ном четырёхволновом взаимодействии на теплой нелинейности в схеме со встречными волнами накачки. Тепловая решётка записывалась излучением CO 2 лазера, вторая волна нак ачки генерировалась He–Ne лазером (λ 1 =0,63 мкм ). В качестве нелинейной среды рассматривался слой ацетона. Экспериментально было зарегистрировано изображение одномерной сетки с диаметром проволоки 35 мкм. Изображение проволоки было размыто до 150 мкм.

Численный анализ выражения ФРТ квазивырож-денного четырехволнового преобразователя излуч е-ния с учетом частот волн накачки, параметров нелинейной среды, взятых из работы [12], показывает, что ширина модуля ФРТ в плоскости оптимальной фокусировки в схеме с плоскими встречными волнами накачки равна 57 мкм. Отстройка плоскости фокусировки сигнальной волны от плоскости оптимальной фокусировки на 3 мм приводит к увеличению ширины мод уля ФРТ до 91 мкм.

Таким образом, сравнение экспериментальных и численных значений разрешений четырехволновых преобразователей излучения показывает их хорошее качественное совпадение.