Использование метода конечных элементов для моделирования резервуара высокого давления из полимера, армированного углеродным волокном

Машиностроение и машиноведение

Original article

Using the Finite Element Method to Simulate a Carbon Fiber Reinforced PolymerPressure Vessel

Imad Rizakalla Antipas B , Alexey G. Dyachenko Ф

Don State Technical University, 1, Gagarin sq., Rostov-on-Don, Russian Federation

Introduction. Over the past decade, global demand for pressure vessels has increased significantly, specifically in such industries as aviation, space, chemical, and oil and gas. Being under the constant impact of high internal pressure, the walls of the tanks are under increased stress, which can cause their sudden destruction. To eliminate this probability and improve the strength characteristics, the tanks are made in the form of metal cylinders with an internal coating of composite material consisting of resin reinforced with carbon fibers. This article aimed at studying the effect of the angle of inclination of carbon fiber on cylindrical tanks and determining the maximum destructive pressure using the finite element method of ANSYS program.

Materials and Methods. Using the ANSYS program, a finite element model of a tank was created. It has a central part, which is a metal cylinder with an internal coating of composite material consisting of polymer reinforced with carbon fibers. At the ends of the tank, spiral wound hemispheres were placed. In these studies, SHELL 99 was used to model the layered composite material. The Tsai-Wu theory was used to determine the pressure tank failure criterion.

Results. The cylindrical tank model was calculated for two types of fiber winding paths: annular and spiral, at different angles of their inclination. The results of the pressure value analysis for different fiber inclination angles showed that, starting from the angle value of 0° and up to 45°, it increased, and then, up to the angle value of 65°, it began to decrease. The critical pressure value for a carbon fiber reinforced tank was 207 MPa, which was obtained at a fiber angle of 45^o.

Discussion and Conclusion. Analysis of the studies showed that at a fiber inclination angle of 45^o, the value of the maximum stress turned out to be the smallest, and the maximum possible destructive pressure at the same angle was 207 MPa. It follows, that the optimal fiber orientation angle to provide safe operation of the high-pressure tank is ± 45^о, and the carbon fiber tank, calculated at the same fiber winding angle, has the maximum strength value.

Введение. Использование резервуаров высокого давления из углеродных волокон нашло широкое распространение в различных областях промышленности из-за своих отличительных свойств, таких как малый вес и высокая прочность. Поэтому в последнее время спрос на такие резервуары существенно возрос в тех случаях, когда вес играет большую роль [1, 2].

Важнейшими областями применения резервуаров такого типа являются аэрокосмическая, авиационная и химическая техника. Кроме того, резервуары, армированные волокном, широко используются для увеличения напора при транспортировке нефти и газа. Во многих случаях резервуары такого назначения подвергаются воздействию высокого внутреннего давления, следствием чего может стать скачкообразное повышение напряжения на стенках сосуда и внезапное их разрушение, что наносит большой ущерб материальным и людским ресурсам [3, 4].

В [5] проведен ряд исследований, направленных только на изучение напорного резервуара из многослойного композита, в ходе которых определена ожидаемая прочность на смятие. В [6] изучалось поведение вращающегося составного напорного резервуара под воздействием внутреннего давления и осевой нагрузки; в [7] проведены исследования по изучению влияния тепловых нагрузок, действующих на многослойный композитный напорный бак. В работе [8] исследовалось поведение многоугольного композитного напорного бака пяти различных форм под действием внутреннего давления различного режима, а в [9] — изучалась работоспособность составного напорного бака при воздействии поперечных нагрузок.

Проектирование резервуара из композитного материала является сложной проблемой, поэтому для проведения полного и точного анализа необходимо выбрать приоритетные факторы. Авторами изучался резервуар высокого давления, армированный несколькими слоями углеродных волокон и подвергаемый нагрузке от внут- реннего давления. Цель работы — изучение влияния угла наклона углеродного волокна на цилиндрические резервуары и определение величины максимального разрушающего давления с использованием метода конечных элементов программы ANSYS.

Материалы и методы. Теоретическое исследование. Резервуар высокого давления из композитных материалов (CFRP) состоит из центральной части, представляющей собой металлический цилиндр с внутренним покрытием, состоящим из полимера, армированного углеродными волокнами. Торцевые поверхности резервуара имеют форму полусфер со спиральной намоткой (рис. 1).

у ^^^^^^^^^^"

Рис. 1. Продольное сечение резервуара

Резервуары, работающие при высоких давлениях и армированные углеродным волокном, изготавливаются методом филаментной намотки (рис. 2). Для получения необходимой стабильности армирования волокна отправляются на движущуюся тележку при тщательном выборе их координации, а затем наматываются на цилиндрическую поверхность. На стабильность координации волокон влияет несколько факторов: температура, форма и обработка поверхности, а также степень сцепления волокон с матрицей. Угол наклона намотки контролируется скоростью перемещения тележки и скоростью вращения цилиндрического барабана. С целью получения высоких эксплуатационных и прочностных свойств внутренняя цилиндрическая поверхность резервуара покрывается несколькими слоями волокон [10].

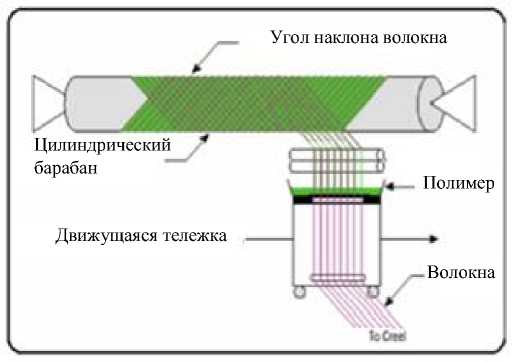
Рис. 2. Схема намотки волокон

Угол наклона волокон оказывает большое влияние на свойства резервуаров, поэтому важным вопросом является поиск соответствующего угла для каждой части резервуара. Угол ориентации волокон определяется необходимой величиной трения между волокнами и слоем композитного материала, как показано в соотношении:

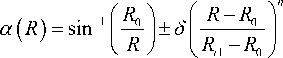
Машиностроение и машиноведение

где R — расстояние между центром и точкой слоя; R — радиус центральной оси; R — радиус по касательной к поверхности цилиндра при 5 = 0 [8].

Критерии разрушения Tsai-Wu. При исследовании и моделировании резервуара высокого давления, выполненного из композитного материала, использовались критерии разрушения по теории Tsai-Wu [11]. Реализация уравнения (1) необходима для исследования ожидаемого разрушения ортотропных материалов по теории Tsai-Wu:

F l u 'll + F 2 ^ 22 + F, ° 12 + ^F il ° 22 + F 66 ^T 12 + ² F n ^ ll ^ 22 = ^1.

Упругие свойства определяются четырьмя независимыми константами:   E11, E22, G12, V12, представленными в таблице 1.

Таблица 1

Характеристики композитного материала LY5052/T300

Свойства	Углеродное волокно Т300	Эпоксид LY5052
Модуль упругости	230 ГПа	3,0 ГПа
Прочность на растяжение	3,5 ГПа	71,0 ГПа
Плотность	1760 г/см3	1,14 г/см3

Силы рассчитываются по следующим уравнениям:

11   111

F=-; F=-; F =0; F =-

1 XX  2 YY 611

=

22 =

; F ₆₆ =

_S ; F ₁₂ =- ₂л/ F 11 F 22 ,

где X — растягивающая сила в продольном направлении; Y — растягивающая сила в поперечном направлении; X_c — сила давления в продольном направлении; Y — сила давления в поперечном направлении; S — сила сдвига.

Максимальное  разрушающее напряжение достигается при выполнении  одного из  следующих соотношений [12]:

^{σ 1} ≥ 1; ^{σ 2} ≥ 1; ^{τ 12} ≥ 1.

XYS

Свойства материалов и моделирование методом конечных элементов. Композитный материал, использованный для исследуемого резервуара, представляет собой полимер, армированный углеродным волокном типа T300, а в качестве полимерного материала применяется эпоксид LY5052. Композитные материалы имеют ортотропную природу, поэтому процесс их моделирования конечными элементами сложнее, чем изотропных материалов, таких как алюминий и сталь.

На рис. 3 представлена конечно-элементная модель резервуара высокого давления из углепластика, внутренний слой которого состоит из алюминиевого сплава, армированного восемью слоями композитного материала Carbon/Epoxy T300/LY5052.

Модель имеет следующие размеры:

• -    длина резервуара —1200 мм;

• -    диаметр резервуара по центру — 300 мм;

• -    общая толщина — 64 мм;

• -    толщина одного слоя — 6,5 мм;

• -    толщина футеровки — 0,12 мм.

  
  
  

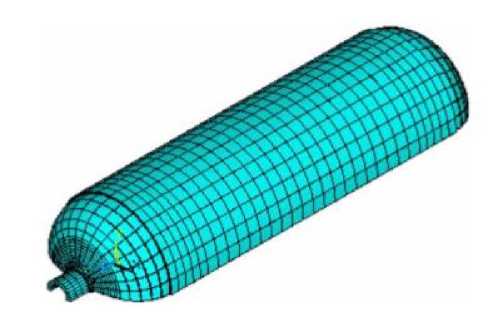
  Рис. 3. Конечно-элементная модель резервуара CFRP

  
  

Для исследования резервуаров высокого давления из композитных материалов очень важно выбрать подходящий тип конечных элементов. Программа ANSYS содержит конечные элементы SHELL и SOLID, необходимые для моделирования слоистых композитных материалов. Для исследования использовали программу SHELL 99, которая ускоряет расчёт конструкции, имеющей до 250 слоев. Этот элемент представляет собой многоуровневую линейную структуру с восемью узлами и шестью степенями свободы и позволяет пользователю определять гибкость, наклон слоев и плотность каждого слоя.

При изучении композитных материалов формирование слоев является одним из основных вопросов, поскольку каждый слой имеет свой угол наклона, а волокна в каждом слое имеют различные углы наклона, поэтому свойства каждого слоя необходимо определять отдельно.

Для формирования слоев требуются характеристики материала, количество слоев, угол наклона волокон, толщина слоя и количество точек интегрирования в каждом слое. Приведем сравнительные сведения о свойствах применяемых материалов: CFRP и алюминия 6061. Плотность: CFRP — 1570 кг/м³, алюминия — 2750 кг/м³. В табл. 2 показаны механические характеристики применяемых материалов: модуль упругости E ; предел прочности при сдвиге G ; предел прочности при растяжении V .

Таблица 2

Механические свойства CFRP и алюминия 6061

Параметры в направлениях координатных осей, ГПа	CFRP	Алюминий 6061
E X	128	7070
E Y	10,5	70
G XY	5	70
G YZ	5
G ZX	5
V XY	0,27	0,3
V YZ	0,4	0,3
V ZX	0,02	0,3

Создана модель с использованием девяти слоёв композитного материала с различными углами наклона волокон:

[+ 25 ° / - 25 ° ] , [+ 30 ° / - 30 ° ] , [+ 35 ° / - 35 ° ] , [+ 40 ° / - 40 ° ] , [+ 45 ° / - 45 ° ] , [+ 50 ° / - 50 ° ] , [+ 55 ° / - 55 ° ] .

На рис. 4 показана последовательность слоев с наклоном волокон под углом ± 45°, реализованная в программе ANSYS.

LAYER STACKING

ELEM     -О

SECT     -1

LAYERS :

TOTAL • -0

shomm i то FROM0

AN

Jul 3261

Layers            Materials

There

-15

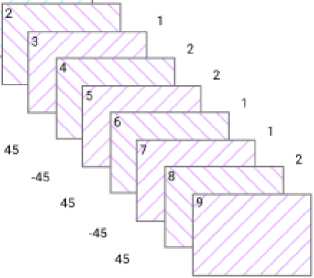
Машиностроение и машиноведение

Рис. 4. Последовательность слоев с наклоном волокон под углом ± 45°

Цифровое моделирование. Расчет напряжений и перемещений . Работа резервуара высокого давления проанализирована с использованием критериев разрушения по теории Tsai-Wu. Для расчета максимальных напряжений и перемещений применялось внутреннее рабочее давление 35 МПа. Наибольшее напряжение резервуара наблюдалось при угле наклона кольцевых волокон — 0° и различных углах наклона спиральных волокон:

[+ 25 o / - 25 o ] , [+ 30 o / - 30 o ] , [+ 35 o / - 35 o ] , [+ 40 o / - 40 o ] , [+ 45 o / - 45 o ] , [+ 50 o / - 50 o ] , [+ 55 o / - 55 o ] .

На рис. 5 показано распределение эквивалентных напряжений и перемещений в резервуаре при угле наклона волокон ± 45°. В таблицах 3, 4 приведены максимальные и минимальные значения перемещений и эквивалентных напряжений в направлениях координатных осей X , Y , Z .

а )                                                     б )

Рис. 5. Эквивалентное распределение в резервуаре: а — напряжений; б — перемещений

Таблица 3

Направление деформации	Минимум, мм	Максимум, мм
суммарная векторная	0	6,473
по оси X	–3,914	3,914
по оси Y	– 6,473	0
по оси Z	–3,906	3,909

Максимальные и минимальные значения перемещений в направлениях осей X , Y , Z

Максимальные и минимальные значения напряжений в направлении осей X , Y , Z

Таблица 4

Направление деформации	Минимум, МПа	Максимум, МПа
суммарная векторная	11,886	463,756
по оси X	– 81,852	528,485
по оси Y	–155,587	341,607
по оси Z	– 80,307	530,07

Определение ожидаемого разрушающего давления и оптимального угла наклона волокон. Нагружение резервуара осуществлялось постепенно увеличивающимся внутренним давлением, начиная с его рабочего значения — 35 МПа. Затем полученное расчетное максимальное напряжение внутреннего давления сравнивали с конечным допускаемым напряжением по условию: «т^ < сги , где: <ттах — расчетное максимальное напряжение; ^ — конечное допускаемое напряжение. Допускаемое напряжение для резервуаров высокого давления из углепластика составляет 1210 МПа.

Модель цилиндрического резервуара рассчитывалась для двух видов путей намотки волокон: кольцевого и спирального, а также при различных углах наклона волокон:

[+ 25 o / - 25 o ] , [+ 30 o / - 30 o ] , [+ 35 o / - 35 o ] , [+ 40 o / - 40 o ] , [+ 45 o / - 45 o ] , [+ 50 o / - 50 o ] , [+ 55 o / - 55 o ] .

При кольцевом пути намотки угол наклона волокон к оси цилиндра составляет 0°. На рис. 6 показана конечно-элементная модель цилиндрического резервуара высокого давления.

Рис. 6. Конечно-элементная модель цилиндрического резервуара высокого давления

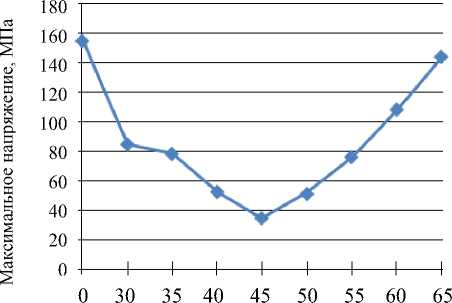
Результаты исследования. На рис. 7 показано изменение максимального напряжения, начиная со значения угла от 0^о и до 45^о оно уменьшается, а затем до значения 65^о возрастает. Установлено, что максимальное напряжение в цилиндрическом резервуаре высокого давления, армированного углеродными волокнами, было наименьшим при угле наклона волокон ± 45^о.

Угол наклона волокна

Рис. 7. Зависимость максимального напряжения от угла наклона волокон

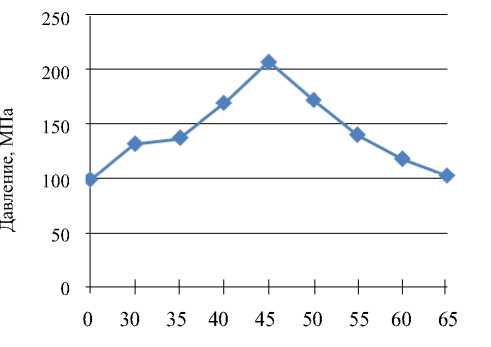
На рис. 8 представлены результаты анализа величины давления для различных углов наклона волокон, которые показывают, что, начиная со значения угла 0^о и до 45^о давление увеличивается, а затем до значения угла 65^о уменьшается. Наибольшее давление, которое может выдержать резервуар, армированный углеволокном без разрушения, составляет 207 Мпа. Это давление имеет место при угле наклона волокон ± 45^о, т. о. оно и является ожидаемым значением разрушающего давления для резервуара.

Машиностроение и машиноведение

Угол наклона волокна

Рис. 8. Зависимость давления от угла наклона волокон

На рис. 9 представлено распределение напряжений в резервуаре с углом наклона волокон ± 45^о, причем максимальное напряжение при приложении давления составляет 1213 МПа и оно выше, чем допускаемое напряжение для резервуаров высокого давления из углепластика, которое составляет 1210 МПа.

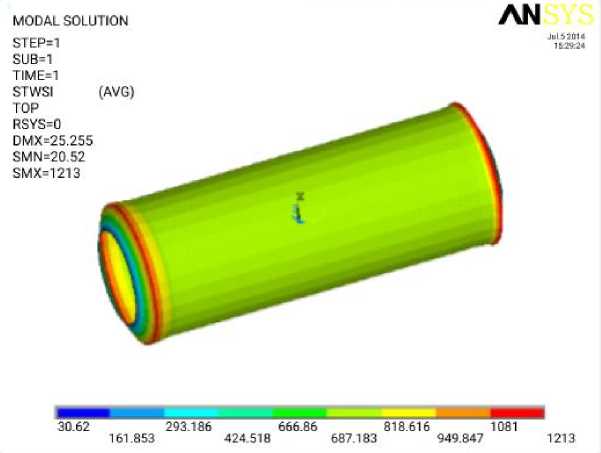
Рис. 9. Распределение напряжений в резервуаре при нагнетании давления и угле наклона волокон ± 45^о

Обсуждение и заключения. Конечно-элементная модель резервуара, армированного углеродным волокном, спроектирована и исследована с использованием программы ANSYS с применением в процессе моделирования элемента SHELL 99. Создано несколько моделей с различными углами наклона волокон. Максимальное напряжение и разрушающее давление для резервуара высокого давления рассчитывались с использованием критериев Tsai-Wu. Установлено, что максимальное напряжение оказалась наименьшим при угле наклона волокон ± 45^о, а максимально возможное разрушающее давление в этих же условиях составило 207 МПа. Это означает, что оптимальный угол наклона волокон для обеспечения безопасной работы резервуара высокого давления составляет ± 45^о, а резервуар из углепластика, рассчитанный с тем же углом намотки волокон, имеет максимальную прочность.