Использование метода наблюдения потока для определения температуры ротора синхронного двигателя с постоянными магнитами

Тяговые приводы, используемые в электрических и гибридных автомобилях, обычно используют синхронные двигатели с постоянными магнитами (СДПМ) с использованием неодимового железа (NdFeB) в качестве материала постоянного магнита. Этот класс синхронных двигателей имеет два основных преимущества перед асинхронной машиной. Этими преимуществами являются более высокая плотность мощности и крутящего момента, а также более высокая эффективность при низких и средних скоростях. С другой стороны, недостатком является температурная чувствительность материала постоянного магнита. Температура оказывает прямое влияние на остаточную плотность магнитного материала, поэтому исследование температуры помогает повысить точность определения расчетного крутящего момента [2].

Прямое измерение температуры постоянного магнита в большинстве случаев нецелесообразно, поскольку информация должна передаваться от ротора к статору предпочтительно с помощью какой-либо беспроводной технологии. В качестве альтернативы существуют три различных способа получения температуры ротора [1]:

• •    тепловое моделирование ;

• •    инжекционный метод ;

• •    наблюдение потока .

С одной стороны, тепловые процессы с сосредоточенными параметрами (ТПСП) дают возможность оценить не только температуру ротора, но также и температуру в нескольких критически важных местах двигателя (например, в лобной части обмотки). С другой стороны, метод ТПСП требует много времени с точки зрения идентификации параметра и основывается на предположениях относительно теплового состояния двигателя. Кроме того, методы не могут быть использованы при любых условиях, так как они вызывают ток нулевой последовательности и, следовательно, пульсацию крутящего момента. Это приведет к дополнительным потерям и усилению колебаний приводной цепи. Более того, работа на более высоких скоростях может быть проблематичной, если сигнал вводимого напряжения приводит к нецелесообразным рабочим циклам. Этот основной метод менее чувствителен к изменяющимся условиям охлаждения или напряжениям промежуточного контура. В дополнение к [1], блок определения температуры ротора улучшен для применения в широком диапазоне скоростей и крутящего момента во время динамической работы. Основополагающим условием для обеспечения точного наблюдения температуры является точная модель машины, так как коэффициент k достаточно мал и поток постоянных магнитов имеет очень малое значение, чтобы получить температурную погрешность не ниже 5 К. Производительность и точность модели машины с дискретным временем сильно зависит от двух аспектов:

• 1.    физическое моделирование ;

• 2.    численное моделирование.

В результате учёта этих двух аспектов получается точная дискретная модель СДПМ. Затем эта модель будет дополнена механизмом обратной связи, позволяющим оценивать изменения намагниченности и температуры ротора соответственно. Моделирование показывает необходимость надлежащей временной дискретизации.

Модель состоит из трёх параметров, где нужно идентифицировать только два. Хотя R (сопротивление статора) довольно просто идентифицировать, нелинейная функция f _dq ( P _dq ) требует немалых усилий для преобразования. Температурный коэффициент kB_r может быть взят из данных паспорта или экспериментальных измерений при холостом ходе.

При данном методе используется модель согласно системе уравнений

^P dq , k   ^{R      P} k ) ^P dq , k — 1 ⁺ T a u dq , k — 1

—

T a R (у k ) Ra

^Ls i dq , k — 1    ;

i dq,k   fdq ^{( p} dq,k ^);

° P k + 1 = P k + 1 ^— P k = " T ;

R(□ Pk+1) = RPpk+1)R 1. Pk), где u - напряжение статора, i - ток статора, " - угловая скорость, р - связанный поток, а T – крутящий момент машины, R – сопротивление статора и обычно нелинейное соотношение fdq между статором и потоком.

Далее добавляется обратная связь, основанная на ошибке между наблюдаемым и измеренным током:

• л       ^ 1  о Л            лл

Pdq, k =      „T^ (idq, k — Idq, k ) + P dq, k—1.

• k 00

л л

Здесь р и i обозначают наблюдаемые величины. Наблюдаемые токи рассчитываются как:

л           лл i dq, к = fd (р dq, k + P dq, k," )

Из выражения (7) абсолютная температура ротора может быть вычислена через:

л

л

O r , k

P d , k ^kBr P p ,0

r ,0 •

Полная структурная схема наблюдателя данного метода изображена на рисунке 1.

Затем необходимо исследовать динамику наблюдателя, чтобы получить соответствующее правило выбора коэффициента обратной связи k .

г Г А - ° Vd _ m3z3 + m2z2 + mlz + mo

G RTO ( z ) ~     =     3     2

Vd    n3 z + n 2 z + n1 z + n0

Передаточная функция дискретного времени (5) действительна, если выполняется линейная зависимость (6)

Vdq = fq (idq ) =

( Ld

I 0 L

⁰ Y i d +^V

■ A ^p

q К i q )

I 0 )

,

где индуктивность L_d и L считаются постоянными в данной рабочей точке. Кроме того, предположение о постоянной скорости — должно быть выполнено. Коэффициенты для выражения (5) задаются как:

• m3 = 0;

• m 2 =^— L q T a k i ;

• m , = 2 L q T_ak i cos — T ) — R s Tk i cos— );

• m ₀ = RT 2 k, cos(^{— Ta} ) — LTk, ;

• 0        s a i                       q a i

• ⁿ 3 = ^Ld^Lq ^;

• n 2 = L d R s T a cos—- ) — L q T a k i — 2 L d L q cos — a ) —

• — L, , L q + L q RT cos— );

• n , = R s T + L d L q + 2 L d Lq cos—T a ) —

• — R s Tk i cos— ) + 2 L q T a k i cos — T ) —

• — 2 L d R s T a cos— ) — 2 L q R s T a cos— );

  
  

n_Q = R_ST 2 k cos( ^— a ) — L_dL_o — LT^ o       s a i                     d q      q a i

—

. о            тТ            тТ

• — Rs-T2 + LdRsTa cos(—a) + LqRsTa cos(—a).

s a    d sa            q sa

Как видно из (5) и (7), поведение зависит исключительно от параметров машины и скорости. Точка максимального значения фазного тока и напряжения теоретически не имеет значения. На практике, однако, эти величины будут играть определенную роль, главным образом, из-за ошибок измерения и дискретизации (ошибка квантования). Структура наблюдателя приведена на рисунке 1. Диаграмма для постоянных параметров машины приведена на рисунке 2.

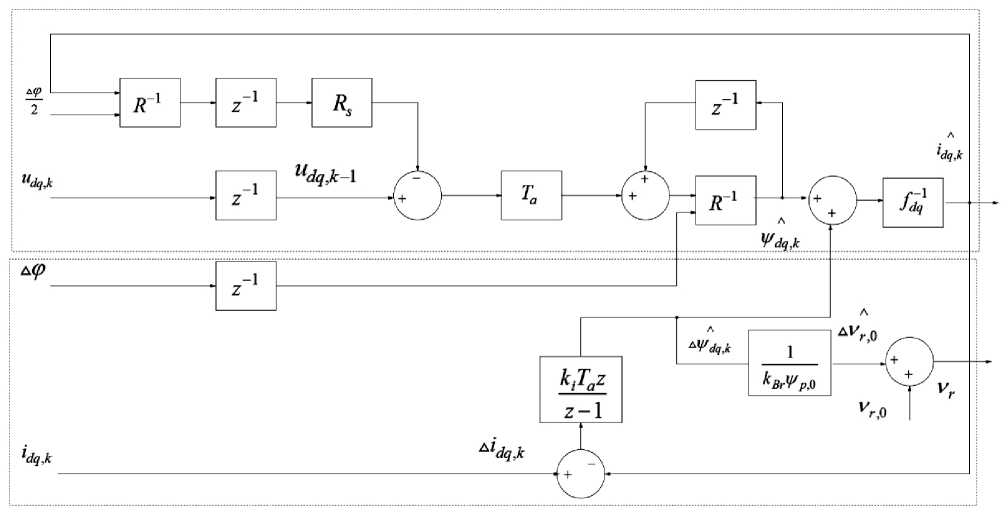
Рис. 1. Структура наблюдателя: верхняя часть модели соответствует выражению (1); нижняя часть служит для создания структуры наблюдателя.

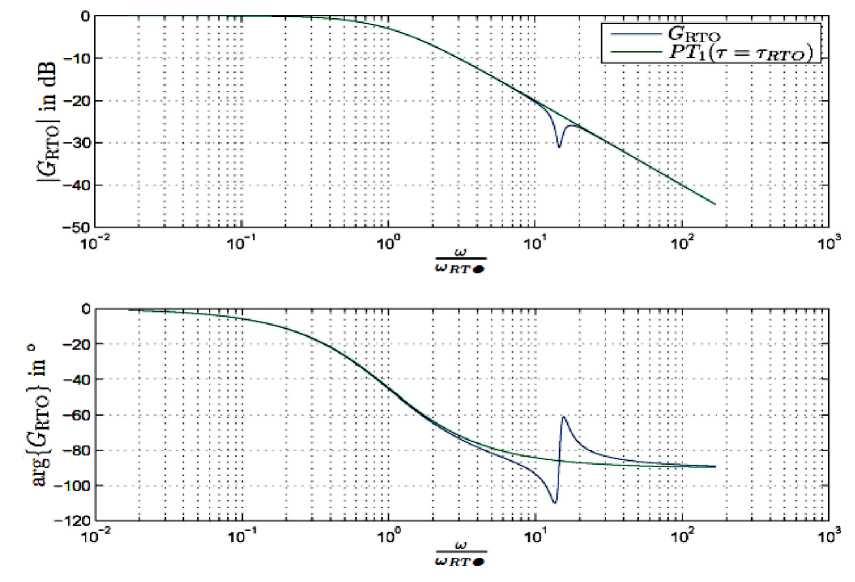
Рис. 2. АЧХ и ФЧХ передаточной функции

GRTO по сравнению

τ с низкочастотным фильтром первого порядка с постоянной времени RTO.

Вывод . Предложен метод определения температуры ротора с использованием дополнительного наблюдателя потока. В качестве обязательного условия была введена модель дискретного электродвигателя. Результаты моделирования показали значительно лучшую дискретизацию по сравнению со стандартными уравнениями первого порядка. Рассмотренный метод может быть легко реализован на часто используемых платформах реального времени, и усилия по идентификации параметров приемлемы. Результаты измерений оказались удовлетворительными для наблюдателей в широком диапазоне скоростей и крутящего момента. Точность наблюдателя сильно коррелирует со скоростью машины и для очень низких скоростей, метод не может быть применен. Это не очень критично, так как тепловая динамика ротора довольно медленная и не значительно возрастает в этом диапазоне скоростей. На средних и высоких скоростях была достигнута абсолютная ошибка наблюдателя ниже 5 К. Таким образом, наблюдатель температуры ротора, по-видимому, применим к широкому спектру тяговых применений.