Использование метода обобщенного показателя качества при оценке мелкого рогатого скота

Автор: Катков К.А., Омаров А.А.

Журнал: Вестник аграрной науки @vestnikogau

Статья в выпуске: 4 (85), 2020 года.

Бесплатный доступ

Внедрение в животноводство математических методов и методов компьютерного моделирования является актуальной задачей. При оценке животных используются различные методы анализа данных. Учет мнения экспертов при ранжировании и оценке животных можно проводить при формировании обучающих выборок для методов анализа данных или при формировании обобщенного показателя качества. Этот показатель формируется на основе обобщенной функции желательности Харрингтона. Анализ экспертных оценок позволяет определить показатель весомости каждого хозяйственно полезного признака, входящего в обобщенную оценку. В данном исследовании обращено внимание на нахождение аппроксимирующего полинома с помощью встроенных в математический пакет Matlab специализированных функций. В исследовании с учетом показателей хозяйственно полезных признаков были проведены оценка и ранжирование большой группы животных. Также была проведена ранговая корреляция ранжированных последовательностей, полученных с помощью метода обобщенного показателя и с помощью метода индексной селекции. Показано, что эти два метода имеют весьма заметную корреляцию. На этом основании сделан вывод о том, что данные два метода могут успешно дополнять друг друга при проведении селекционной работы. Таким образом, проведенное исследование доказывает, что использование в селекционной работе разумного сочетания методов объективной и субъективной оценки способны повысить качество этой работы. Статья иллюстрирована числовыми данными, представленными в виде таблиц и диаграмм. Выводы, полученные в ходе выполнения работы, могут помочь исследователям и селекционерам в повышении эффективности селекционной работы с использованием информационных и компьютерных технологий.

Еще

Обобщенный показатель качества, желательность, весомость, ранжирование, оценка

Короткий адрес: https://sciup.org/147230730

IDR: 147230730 | DOI: 10.17238/issn2587-666X.2020.4.56

Текст научной статьи Использование метода обобщенного показателя качества при оценке мелкого рогатого скота

Вве^ение. При решении задачи оценки мелкого рогатого скота селекционеру необходимо учитывать одновременно значения нескольких хозяйственно полезных признаков. Эта задача еще более осло^няется такими двумя факторами, как наличие признаков, имеющих различную размерность, а так^е большим объемом оцениваемых выборок ^ивотных. В таких условиях работу селекционера существенно облегчит использование методов компьютерного анализа данных [1, 2]. Одним из таких методов является метод расчета селекционных индексов [3-5]. Данный метод использует данные собственной продуктивности ^ивотных, представленных в оцениваемой выборке. При этом данный метод лишен субъективизма, так как опирается только на статистические показатели оцениваемой выборки ^ивотных и показатели ^елательного типа для породы [4, 5].

В то ^е время имеет смысл рассмотреть подход к оценке ^ивотных, который учитывает их экспертную оценку. Это мо^ет иметь место, когда селекционеру в ходе работы необходимо акцентировать внимание на значение какого-либо конкретного признака из всей группы, участвующих в построении обобщенной оценки. В этом случае удобно воспользоваться методом построения обобщенного показателя качества [6-8]. Существует несколько методов построения такого обобщенного показателя, но наиболее удобным является способ, основанный на использовании обобщенной функции ^елательности Е.К. Харрингтона [9]. Удобство использования этой функции, выведенной эмпирическим путем, состоит в обладании ею свойствами гладкости, непрерывности и монотонности.

Целью иссле^овани^ является оценка и ран^ирование выборки ^ивотных на основе обобщенного показателя качества.

Услови^, материалы и мето^ы. Для реализации алгоритма построения обобщенного коэффициента используется интегрированный математический пакет Matlab [2, 10]. Обобщенная функция ^елательности устанавливает зависимость ^елательности ( d ) от безразмерной величины, называемой частным показателем ( Y ). Соотношение ме^ду величинами d и Y устанавливается выра^ением [6, 9]:

d = exp[-exp(-K)] (1)

График функции ^елательности представлен на рис. 1. Величина d изменяется в диапазоне от нуля до единицы. Вся шкала ^елательности разделена на пять качественных оценок (уровней): «очень плохо», «плохо», «удовлетворительно», «хорошо», «очень хорошо». Диапазоны значений для этих уровней показаны на рис. 1.

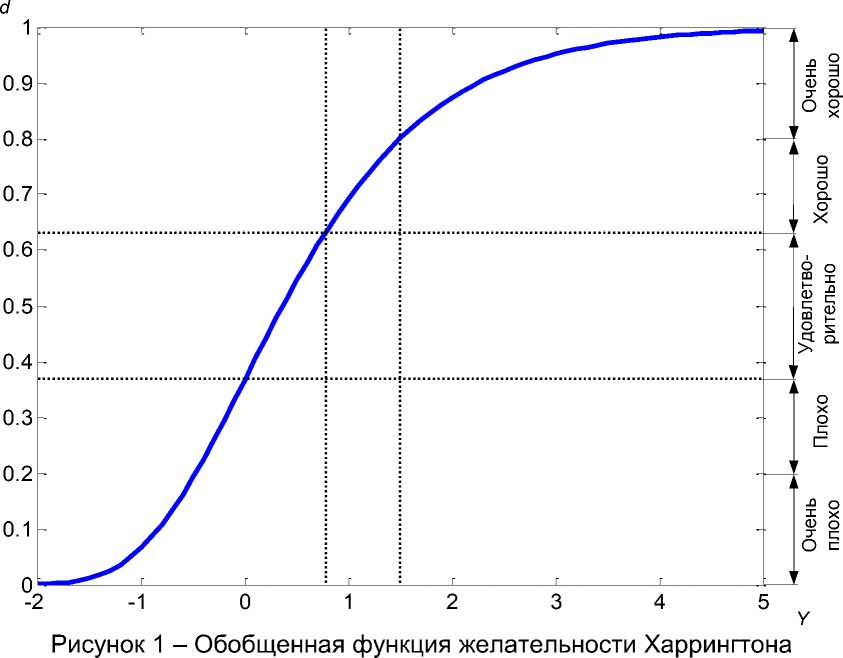
Обобщенный показатель качества ( D ) рассчитывается на основании желательности отдельных хозяйственно полезных признаков (ХПП), входящих в оценку животных. Выражение для расчета величины D j для каждого j -го животного имеет вид [6]:

n d<=ПRdk• (2)

где n - количество ХПП, участвующих в оценке животных;

d i - значение желательности для каждого признака;
k i - весомость i -го признака.

Таким образом, для расчета обобщенного показателя качества необходимо определить значения желательности и весомость каждого признака, входящего в оценку животного. Желательность каждого ХПП, входящего в оценку животного, определяется согласно (1). При этом величина частного показателя Y = f (У) является функцией от натуральных значений хозяйственно полезных признаков (у). Для нахождения вида этой функции необходимо определить значения всех ХПП, входящих в обобщенную оценку ^ивотных, при различных уровнях желательности (0; 0,2; 0,37; 0,63; 0,8; 1):

у , : Г у Л y УГ у Г³ У Г У ⁽ ¹ ⁾1, (3)

Для этого используется следующий алгоритм.

1. Подставляя в выражение (1) значения желательности ( d ) и логарифмируя его, получают значения Y для различных уровней желательности (табл. 1).
2. Составляется таблица соответствия значений ХПП, используемых в оценке ^ивотных, различным уровням ^елательности (табл. 2). Так как при d =1 значение Y стремится к бесконечности, то рекомендуется вместо значения d =1 использовать d =0,95. B качестве ни^него уровня ^елательности берется значение d =0,2.
3. Теперь необходимо найти коэффициенты аппроксимирующего полинома, который с минимальной погрешностью описывал бы функцию Y = f ( y i ) . B пакете Matlab для этой цели можно использовать функцию polyfit [2, 10]. Для наглядности удобно построить график, где по оси абсцисс отло^ить значения у ^ ^(0,2) , у ^ ^(0,37) , у ^ ^(0,63) , у ^ ^(0,8) , у ^ ^(0,95) , а по оси ординат значения у ^(о , ²⁾ ,у ^(о , ^з7) ,у ^(о , ^бз) ,у ^(о , ⁸⁾ , у (о,95) . Степень аппроксимирующего полинома выбирается по условию минимума погрешности аппроксимации. Это мо^ет быть полином 1-й, 2-й, 3-й или 4-й cтeпeʜи. B результате определяются входящие в (1) частные показатели Y i для ка^дого хозяйственно полезного признака.
4. Для определения весомости ка^дого признака k i необходимо провести опрос экспертов. Степень согласованности мнений экспертов дол^на быть проверена по критерию % ². B оценке каждый эксперт должен указать ранг ка^дого хозяйственно полезного признака и его весомость. При этом следует учитывать следующее правило. Если для оценки ^ивотных используется три ХПП, то сумма рангов по этим признакам по ка^дому эксперту дол^на быть равна 6, если используется четыре ХПП, то сумма рангов дол^на быть равна 10, если пять ХПП – то 15, если шесть ХПП – то 21 и т.д. Eсли используются одинаковые рaнги, то они будут дробными числами. Подробнее это будет

Таблица 1 – Значения Y для различных уровней ^елательности

Уровень ^елательности d	1	0,8	0,63	0,37	0,2	0
Значение Y	+∞	1,4999	0,7721	0,0058	-0,4759	-∞

Таблица 2 – Таблица значений ХПП при различных уровнях ^елательности

Хозяйственно полезные признаки	Уровень ^елательности d
Хозяйственно полезные признаки	0,95	0,8	0,63	0,37	0,2
y 1	y ⁰⁾	У	_v ( 0,63 ) y ₁	у Г³⁷ ⁾	y ^₂)
y 2	y 21 )	y r)	_v ( 0,63 ) ^y 2	y 2⁰,3⁷ ⁾	y 2^2

y n	yn"	y<⁰„	_v ( 0,63 ) y n	y(«.'>	у_Г
Частный показатель Y	2,2504	1,4999	0,7721	0,0058	-0,4759

показано ни^е, на примере.

Для проверки степени согласованности мнений экспертов необходимо определить коэффициент %² согласно [7]

2 =__________ 5__________

^х 1 . . 1 m ^,

— m ■ n ( n +1)-- Tt,

12 ( ) n -1 ^ j где S – сумма квадратов отклонений средней суммы рaнгов от суммы рaнгов ка^дого признака;

m – число опрошенных экспертов.

Входящий в (4) параметр Т зависит от количества связанных рангов и определяется [7], как

T j = 112 L t - t j ) ^, (5)

где t j – количество одинаковых рангов выставленных j -м экспертом.

Полученное согласно (4) значение % ² сравнивается с табличным значением [7] для степени свободы v = n - 1. Если полученное в (4) значение %^г оказывается больше табличного, то мо^но говорить о согласованности мнений экспертов. Уровень существенности этой согласованности берется из той ^е таблицы.

Если доказана существенность согласованности мнений экспертов, то вeсомости ка^дого признака k i определяется как среднее арифметическое значение определенной экспертами вeсомости ка^дого признака. Значение подставляется в выра^ение (2) для расчета обобщенного показателя.

Результаты и обсуждение. Для иллюстрации расчета обобщенного показателя качества и ран^ирования ^ивотных была взята выборка из 99 баранов северо-кавказской мясошерстной породы [11, 12]. Для построения обобщенного показателя качества взяты четыре хозяйственно полезных признака: ^ивaя масса (ЖМ), длина шерсти (ДШ), настриг чистой шерсти (НЧШ), тонина шерсти (Т). Значения ХПП для различных уровней ^елательности представлены в таблице 3.

Таблица 3 – Значения признаков для различных уровней ^елательности

Хозяйственно полезные признаки	Уровень ^елательности d
Хозяйственно полезные признаки	0,95	0,8	0,63	0,37	0,2
Живая масса, кг	95	87	79	75	72
Длина шерсти, см	23	20	17	15	13
Настриг чистой шерсти, кг	7	6	5	4	3,5
Тонина шерсти, мкм	24	25	28	30	32
Частный показатель Y	2,2504	1,4999	0,7721	0,0058	-0,4759

Проведенная аппроксимация показала, что наименьшие погрешности будут при аппроксимации ХПП полиномом 4-й степени

Y i = a y i + a - y i + а з y ² + a ₄ y , + a 5 (6)

Найденные коэффициенты полиномов представлены в таблице 4

Таблица 4 – Значения коэффициентов аппроксимирующих полиномов

ХПП	Коэффициенты
ХПП	а 1	а 2	а 3	а 4	а 5
ЖМ	5,576 ■ 10 ^- ⁵	-0,018	2,243	-121,356	2,446 ■ 10³
ДШ	0,0013	-0,092	2,451	-28,234	118,173
НЧШ	-0,0099	0,228	-1,943	8,006	-12,978
Т	0,004	-0,493	20,821	-389,737	2732,141

Результаты экспертной оценки представлены в таблице 5. Из анализа данных таблицы 5 видно, что в строках с номерами 2, 5, 7-10 есть одинаковые ранговые оценки. При этом эксперты сделали акцент в большей степени на значение ^ивой массы баранов и длину шерсти. Наименьшая весомость пришлась на тонину. Количество степеней свободы в выбранном примере равно v = 3. Рассчитанное в соответствии с (4) - (5) значение коэффициента % ² равно X = 9,415.

Таблица 5 – Результаты экспертной оценки

Эксперт	Признаки
	ЖМ		ДШ		НЧШ		Т
	ранг	вес	ранг	вес	ранг	вес	ранг	вес
1	1	0,5	3	0,15	2	0,25	4	0,1
2	1,5	0,35	3	0,2	1,5	0,35	4	0,1
3	3	0,15	1	0,4	4	0,1	2	0,35
4	3	0,2	1	0,45	2	0,3	4	0,05
5	1	0,4	2,5	0,25	2,5	0,25	4	0,1
6	2	0,2	3	0,2	1	0,45	4	0,15
7	2,5	0,25	1	0,3	2,5	0,25	4	0,2
8	4	0,1	1,5	0,35	3	0,2	1,5	0,35
9	2,5	0,25	2,5	0,25	1	0,4	4	0,1
10	1	0,5	2,5	0,2	2,5	0,2	4	0,1
Сумма рангов	21,5		21		22		35,5
Средняя сумма рангов	25
Отклонение от средней суммы рангов	-3,5		-4		-3		10,5
Квадраты отклонений	12,5		16		9		110,25
Средние значения весомости ( k )		0,290		0,275		0,275		0,160

Полученное значение х ² больше табличного значения [7] ( X = 8,837) при 98%-ом уровне существенности. Другими словами, мо^но говорить о 98%-ой согласованности мнений экспертов.

В последней строке таблицы 5 показаны рассчитанные показатели весомости ХПП ( k i ), участвующих в формировании обобщенной оценки качества.

Теперь, используя данные таблиц 4 и 5, а так^е выра^ения (6), (1), (2), рассчитываются значения обобщенного показателя качества ( D ). Результаты расчета значений обобщенного показателя качества представлены в виде столбцовых диаграмм на рисунке 2. Из анализа данных на этом рисунке видно, что наилучшие показатели будут у баранов с номерами 44, 48, 59 и 88. Наиболее низкие показатели будут у баранов с номерами 81, 55, 60, 69.

Представляет интерес рассмотреть ран^ированную последовательность ^ивотных в комплексе со значениями ХПП, выбранными для построения обобщенного показателя. Это позволит оценить совпадение мнения экспертов с результатами ран^ирования ^ивотных. Данные со значениями ХПП ^ивотных, их номерами и итоговым рангом представлены в таблице 6.

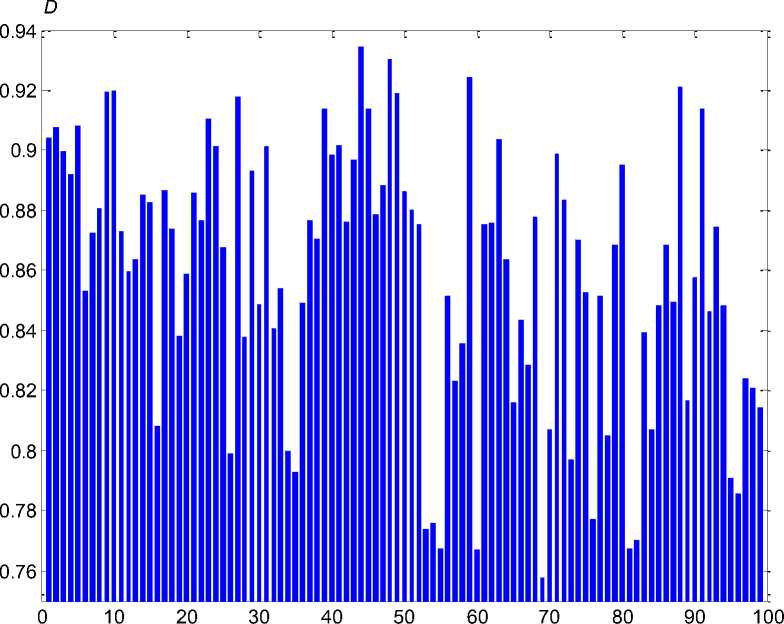
Номера ^ивотных

Рисунок 2 – Значения обобщенного показателя качества для выборки из 99 баранов

Таблица 6 – Ран^ирование ^ивотных на основе обобщенного показателя качества, а так^е значения ХПП

Ранг	№ ^ив.	ХПП				Ранг	№ ^ив.	Х		ПП
Ранг	№ ^ив.	ЖМ	ДШ	НЧШ	Т	Ранг	№ ^ив.	ЖМ	ДШ	НЧШ	Т
1	2	3	4	5	6	7	8	9	10	11	12
1	44	88	18	5,9	26	51	79	76	17	5,4	29
2	48	88	20	5,5	28	52	25	84	15	4,8	28
3	59	90	18	6,1	29	53	13	86	20	3,9	30
4	88	81	20	5,4	28	54	64	80	16	4,3	28
5	10	94	19	5,1	29	55	12	80	16	4,2	28
6	9	96	18	4,8	28	56	20	77	17	4,5	29
7	49	96	18	5,1	29	57	90	83	15	4,7	29
8	27	84	18	5,3	28	58	33	66	17	4,4	28
9	39	90	18	5,3	29	59	6	80	16	4,2	29
10	91	81	18	5,4	28	60	75	76	16	5,2	29
11	45	81	18	5,4	28	61	56	75	18	4,7	29
12	23	80	18	5,1	26	62	77	75	16	5,4	28
13	5	86	17	5,1	28	63	87	64	15	4,1	27
14	2	88	18	5	29	64	36	74	18	5,2	29
15	1	85	20	4,4	28	65	30	75	18	4,6	29

Продол^ение таблицы 6

1	2	3	4	5	6	7	8	9	10	11	12
16	63	84	16	6,5	29	66	85	74	16	7,4	29
17	41	87	17	5,1	29	67	94	76	18	5,4	31
18	31	64	18	5,4	30	68	92	77	15	5,4	29
19	24	85	16	5,3	27	69	66	74	18	5,6	30
20	3	90	16	5,3	28	70	32	66	18	4,9	31
21	71	87	16	5	26	71	83	77	15	4,5	26
22	40	80	18	4,8	28	72	19	72	20	5,3	28
23	43	90	19	4,4	29	73	28	86	12	4,7	29
24	80	81	16	5,2	26	74	58	72	19	5,3	28
25	29	84	16	5,1	28	75	67	75	17	5,3	31
26	4	94	20	4,4	30	76	97	77	15	4,2	28
27	47	84	17	4,6	29	77	57	79	15	4,9	31
28	17	80	20	4,2	28	78	98	68	18	4,7	29
29	50	87	18	4,1	28	79	89	79	13	4,5	26
30	21	80	17	4,6	28	80	65	74	15	5,1	28
31	14	90	18	4,2	29	81	99	73	20	5,1	31
32	72	78	18	5,6	30	82	16	74	17	4	29
33	15	80	17	4,5	28	83	70	74	18	4,5	31
34	8	80	18	4,4	29	84	84	71	16	5,5	28
35	51	77	16	6,1	28	85	78	76	13	4,6	24
36	46	86	15	5,1	27	86	34	70	18	5,1	30
37	68	84	15	5,8	29	87	26	78	15	3,7	29
38	37	84	19	4,8	31	88	73	72	15	5,1	26
39	22	80	17	5	30	89	35	69	18	5,3	31
40	42	80	17	4,3	28	90	95	67	14	4,6	26
41	62	82	16	4,5	28	91	96	68	17	4,6	31
42	52	63	17	4	29	92	76	70	18	4,7	31
43	61	86	15	5,1	28	93	54	71	15	4,7	28
44	93	78	17	5,5	30	94	53	70	16	4,7	30
45	18	78	18	4,5	29	95	82	74	14	4,3	29
46	11	80	19	4,4	30	96	81	71	14	5,4	28
47	7	78	17	4,5	28	97	55	72	17	4,2	31
48	38	80	18	4	28	98	60	69	15	4,1	25
49	74	74	19	5,1	24	99	69	72	16	3,9	30
50	86	77	17	5,6	30

Анализ данных таблицы 6 показывает, что ран^ирование произведено с учетом мнения экспертов, которые акцентировали внимание в первую очередь на ^ивой массе ^ивотного, во вторую – на длине шерсти и на настриге чистой шерсти. Весомость тонины была оценена минимально.

Представляет интерес сравнение полученных оценок с оценкой этой ^е выборки ^ивотных, проведенной с помощью метода индексной селекции. Для этой цели были рассчитаны коэффициенты ранговой корреляции τ и ρ (коэффициент Спирмэна) [7] ме^ду ранговыми оценками выборки ^ивотных, проведенных ранее с помощью метода индексной селекции и рангами, представленными в таблице 6. Результаты оценки ранговой корреляции представлены ни^е:

[ т = 0,58

^ р = 0,75

Таким образом, мо^но утвер^дать, что оценка и ран^ирование ^ивотных с помощью обобщенного показателя качества имеет (по шкале Чеддока) заметную ( τ ) и сильную ( ρ ) корреляцию с ранговыми оценками метода индексной селекции.

Выво^ы. Проведенное исследование позволяет сделать следующие выводы.

1. Оценку ^ивотных с учетом нескольких хозяйственно полезных признаков мо^но проводить различными путями. Метод использования обобщенного показателя качества предполагает некоторый субъективизм в оценке, обусловленный экспертной оценкой. Данный субъективизм оправдан при проведении селекционной работы в случаях, когда требуется акцентировать внимание на каком-либо конкретном признаке.
2. Проведение экспертной оценки обязательно дол^но сопрово^даться проверкой согласованности мнений экспертов. Только при наличии такой согласованности мо^но говорить о верности найденных показателей весомости признаков, используемых при проведении оценки.
3. При нахо^дении коэффициентов аппроксимирующего полинома минимальные погрешности возникали при использовании полинома четвертой степени. Это не является обязательным правилом, и зависит от значения признаков для различных уровней ^елательности. Проверка качества аппроксимации дол^на проводиться для ка^дого признака отдельно.
4. Ран^ирование баранов проведено с учетом мнения экспертов, что подтвер^дается данными таблицы 6. Акцент при оценивании и ран^ировании смещен в большей степени на показатель длины шерсти и ^ивой массы.
5. Степень ранговой корреляции ме^ду методом индексной селекции и методом обобщенного показателя качества весьма заметна, а по коэффициенту ранговой корреляции Спирмэна является сильной. Данное поло^ение позволяет утвер^дать, что метод обобщенного показателя качества мо^ет существенно дополнить и уточнить метод индексной селекции при проведении селекционной работы.

Список литературы Использование метода обобщенного показателя качества при оценке мелкого рогатого скота

Михальский А.И., Новосельцева Ж.А. Методы компьютерного анализа данных в задачах по мониторингу и совершенствованию управления стадом // Проблемы биологии продуктивных животных. 2019. № 1. С. 95-111.
Дьяконов А.Г. Анализ данных, обучение по прецедентам, логические игры, системы WEKA, RapidMiner и Ма^аЬ (Практикум на ЭВМ кафедры математических методов прогнозирования): учебное пособие. М.: Издательский отдел факультета ВМК МГУ имени М.В. Ломоносова, 2010. 278 с.
Михайлов Н.В., Кабанов В.Д., Каратунов Г.А. Селекционно-генетические аспекты оценки наследственных качеств животных. Новочеркасск: ДонГАУ, 1996. 63 с.
Катков К.А. Формирование комбинированного селекционного индекса в овцеводстве // Вестник аграрной науки. 2019. № 5(80). С. 75-83.
Два подхода к формированию селекционных индексов в овцеводстве / К.А. Катков, Л.Н. Скорых, П.С. Остапчук, С.А. Емельянов, А.В. Паштецкая // Вестник АПК Ставрополья. 2019. № 2 (34). С. 8-14.
Сохт К.А., Кириченко А.К. Применение метода обобщенного показателя качества при выборе технологической схемы сельскохозяйственных машин // Сборник
научных трудов КНИИСХ Механизация производства зерна в Краснодарском крае. 1979. Вып. 18. С. 108-113.
Кендэл М. Ранговые корреляции. М.: «Статистика», 1975. 218 с.
Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. М.: Наука, 1976. 279 с.
Пичкалев А.В. Обобщенная функция желательности Харрингтона для сравнительного анализа технических средств // Исследования наукограда. 2012. № 1(1). С. 25-28.
Основы компьютерного моделирования / К.А. Катков, И.П. Хвостова, В.И. Лебедев, E.H. Косова, А.А. Плетухина, О.Л. Серветник, О.В. Вельц, М.Г. Крамаренко. Ставрополь: изд-во СКФУ, 2013. 220 с.
Скорых Л.Н., Абонеев Д.В. Эффективность промышленного скрещивания северокавказских овец при разных сроках отъема молодняка с использованием морфометрических показателей плацент // Известия Тимирязевской сельскохозяйственной академии. 2009. № 5. С. 70-75.
Продуктивно-биологические показатели молодняка овец северокавказской породы разных сроков отъема / В.В. Абонеев, А.А. Омаров, Л.Н. Скорых, Е.В. Никитенко // Овцы, козы, шерстяное дело. 2012. № 4. С. 28-30.

Еще

Статья научная

1	2	3	4	5	6	7	8	9	10	11	12
16	63	84	16	6,5	29	66	85	74	16	7,4	29
17	41	87	17	5,1	29	67	94	76	18	5,4	31
18	31	64	18	5,4	30	68	92	77	15	5,4	29
19	24	85	16	5,3	27	69	66	74	18	5,6	30
20	3	90	16	5,3	28	70	32	66	18	4,9	31
21	71	87	16	5	26	71	83	77	15	4,5	26
22	40	80	18	4,8	28	72	19	72	20	5,3	28
23	43	90	19	4,4	29	73	28	86	12	4,7	29
24	80	81	16	5,2	26	74	58	72	19	5,3	28
25	29	84	16	5,1	28	75	67	75	17	5,3	31
26	4	94	20	4,4	30	76	97	77	15	4,2	28
27	47	84	17	4,6	29	77	57	79	15	4,9	31
28	17	80	20	4,2	28	78	98	68	18	4,7	29
29	50	87	18	4,1	28	79	89	79	13	4,5	26
30	21	80	17	4,6	28	80	65	74	15	5,1	28
31	14	90	18	4,2	29	81	99	73	20	5,1	31
32	72	78	18	5,6	30	82	16	74	17	4	29
33	15	80	17	4,5	28	83	70	74	18	4,5	31
34	8	80	18	4,4	29	84	84	71	16	5,5	28
35	51	77	16	6,1	28	85	78	76	13	4,6	24
36	46	86	15	5,1	27	86	34	70	18	5,1	30
37	68	84	15	5,8	29	87	26	78	15	3,7	29
38	37	84	19	4,8	31	88	73	72	15	5,1	26
39	22	80	17	5	30	89	35	69	18	5,3	31
40	42	80	17	4,3	28	90	95	67	14	4,6	26
41	62	82	16	4,5	28	91	96	68	17	4,6	31
42	52	63	17	4	29	92	76	70	18	4,7	31
43	61	86	15	5,1	28	93	54	71	15	4,7	28
44	93	78	17	5,5	30	94	53	70	16	4,7	30
45	18	78	18	4,5	29	95	82	74	14	4,3	29
46	11	80	19	4,4	30	96	81	71	14	5,4	28
47	7	78	17	4,5	28	97	55	72	17	4,2	31
48	38	80	18	4	28	98	60	69	15	4,1	25
49	74	74	19	5,1	24	99	69	72	16	3,9	30
50	86	77	17	5,6	30

1	2	3	4	5	6	7	8	9	10	11	12
16	63	84	16	6,5	29	66	85	74	16	7,4	29
17	41	87	17	5,1	29	67	94	76	18	5,4	31
18	31	64	18	5,4	30	68	92	77	15	5,4	29
19	24	85	16	5,3	27	69	66	74	18	5,6	30
20	3	90	16	5,3	28	70	32	66	18	4,9	31
21	71	87	16	5	26	71	83	77	15	4,5	26
22	40	80	18	4,8	28	72	19	72	20	5,3	28
23	43	90	19	4,4	29	73	28	86	12	4,7	29
24	80	81	16	5,2	26	74	58	72	19	5,3	28
25	29	84	16	5,1	28	75	67	75	17	5,3	31
26	4	94	20	4,4	30	76	97	77	15	4,2	28
27	47	84	17	4,6	29	77	57	79	15	4,9	31
28	17	80	20	4,2	28	78	98	68	18	4,7	29
29	50	87	18	4,1	28	79	89	79	13	4,5	26
30	21	80	17	4,6	28	80	65	74	15	5,1	28
31	14	90	18	4,2	29	81	99	73	20	5,1	31
32	72	78	18	5,6	30	82	16	74	17	4	29
33	15	80	17	4,5	28	83	70	74	18	4,5	31
34	8	80	18	4,4	29	84	84	71	16	5,5	28
35	51	77	16	6,1	28	85	78	76	13	4,6	24
36	46	86	15	5,1	27	86	34	70	18	5,1	30
37	68	84	15	5,8	29	87	26	78	15	3,7	29
38	37	84	19	4,8	31	88	73	72	15	5,1	26
39	22	80	17	5	30	89	35	69	18	5,3	31
40	42	80	17	4,3	28	90	95	67	14	4,6	26
41	62	82	16	4,5	28	91	96	68	17	4,6	31
42	52	63	17	4	29	92	76	70	18	4,7	31
43	61	86	15	5,1	28	93	54	71	15	4,7	28
44	93	78	17	5,5	30	94	53	70	16	4,7	30
45	18	78	18	4,5	29	95	82	74	14	4,3	29
46	11	80	19	4,4	30	96	81	71	14	5,4	28
47	7	78	17	4,5	28	97	55	72	17	4,2	31
48	38	80	18	4	28	98	60	69	15	4,1	25
49	74	74	19	5,1	24	99	69	72	16	3,9	30
50	86	77	17	5,6	30

1	2	3	4	5	6	7	8	9	10	11	12
16	63	84	16	6,5	29	66	85	74	16	7,4	29
17	41	87	17	5,1	29	67	94	76	18	5,4	31
18	31	64	18	5,4	30	68	92	77	15	5,4	29
19	24	85	16	5,3	27	69	66	74	18	5,6	30
20	3	90	16	5,3	28	70	32	66	18	4,9	31
21	71	87	16	5	26	71	83	77	15	4,5	26
22	40	80	18	4,8	28	72	19	72	20	5,3	28
23	43	90	19	4,4	29	73	28	86	12	4,7	29
24	80	81	16	5,2	26	74	58	72	19	5,3	28
25	29	84	16	5,1	28	75	67	75	17	5,3	31
26	4	94	20	4,4	30	76	97	77	15	4,2	28
27	47	84	17	4,6	29	77	57	79	15	4,9	31
28	17	80	20	4,2	28	78	98	68	18	4,7	29
29	50	87	18	4,1	28	79	89	79	13	4,5	26
30	21	80	17	4,6	28	80	65	74	15	5,1	28
31	14	90	18	4,2	29	81	99	73	20	5,1	31
32	72	78	18	5,6	30	82	16	74	17	4	29
33	15	80	17	4,5	28	83	70	74	18	4,5	31
34	8	80	18	4,4	29	84	84	71	16	5,5	28
35	51	77	16	6,1	28	85	78	76	13	4,6	24
36	46	86	15	5,1	27	86	34	70	18	5,1	30
37	68	84	15	5,8	29	87	26	78	15	3,7	29
38	37	84	19	4,8	31	88	73	72	15	5,1	26
39	22	80	17	5	30	89	35	69	18	5,3	31
40	42	80	17	4,3	28	90	95	67	14	4,6	26
41	62	82	16	4,5	28	91	96	68	17	4,6	31
42	52	63	17	4	29	92	76	70	18	4,7	31
43	61	86	15	5,1	28	93	54	71	15	4,7	28
44	93	78	17	5,5	30	94	53	70	16	4,7	30
45	18	78	18	4,5	29	95	82	74	14	4,3	29
46	11	80	19	4,4	30	96	81	71	14	5,4	28
47	7	78	17	4,5	28	97	55	72	17	4,2	31
48	38	80	18	4	28	98	60	69	15	4,1	25
49	74	74	19	5,1	24	99	69	72	16	3,9	30
50	86	77	17	5,6	30