ИСПОЛЬЗОВАНИЕ МЕТОДОВ МАШИННОГО ОБУЧЕНИЯ ДЛЯ ПРОГНОЗИРОВАНИЯ ВРЕМЕННЫХ РЯДОВ: СОВРЕМЕННЫЕ ПОДХОДЫ И ПЕРСПЕКТИВЫ

Временной ряд представляет собой последовательность значений наблюдаемой переменной, зарегистрированных через одинаковые интервалы времени. Исследование таких рядов проводится с целью прогнозирования будущих значений на основе прежних наблюдений, понимания основных закономерностей или краткого описания ключевых характеристик ряда. Данная статья фокусируется на проблеме прогнозирования, которое играет решающую роль во многих сферах, включая экономику, финансы, бизнес-аналитику, метеорологию и телекоммуникации. Важным аспектом в прогнозировании является длина горизонта прогнозирования, так как многоэтапное прогнозирование усложняется накоплением ошибок, снижением точности и ростом неопределенности.

Традиционно в прогнозировании применялись линейные статистические методы, такие как модели ARIMA (Autoregressive Integrated Moving Average), однако с конца 1970-х годов стало очевидно, что данные методы не всегда подходят для практических применений [1; 2]. В это время были предложены нелинейные модели, такие как билинейная модель, пороговая авторегрессионная модель и модель авторегрессионной условной гетероскедастич-ности (Autoregressive Conditional Heteroscedasticity, ARCH) [3]. Однако по сравнению с линейными моделями, исследование и применение нелинейных моделей находятся на начальном этапе [4].

На протяжении последних двух десятилетий модели машинного обучения стали набирать популярность и зарекомендовали себя как конкурентоспособные альтернативы классическим статистическим моделям [5]. Эти модели, называемые также «черными ящиками» или моделями, управляемыми данными, являются примерами непараметрических нелинейных моделей, использующих исключительно исторические данные для выявления взаимосвязей между прошлыми и будущими значениями [6; 7]. Например, исследования П.Ж. Вербоса показали, что искусственные нейронные сети (ИНС) превосходят традиционные подходы, такие как линейные регрессии и модели Бокса-Дженкинса. А. Лапедес и Р. Фарбер также обнаружили, что ИНС могут быть успешно использованы для моделирования и прогнозирования нелинейных временных рядов [8]. В дальнейшем появились и другие методы, такие как деревья решений, машины опорных векторов и регрессия ближайших соседей.

Настоящая работа представляет обзор методов машинного обучения с акцентом на формализацию задач одношагового прогнозирования и применение методов локального обучения, фрактальных методов и обучения с учителем. В работе систематизированы современные подходы к переходу от одношагового к многошаговому прогнозированию и исследованы возможности их применения с использованием методов локального обучения.

Целью данной работы является изучение и систематизация современных подходов машинного обучения для прогнозирования временных рядов, с акцентом на анализ методов локального обучения, их возможностей и ограничений, а также разработка рекомендаций по применению данных методов в задачах прогнозирования.

Структура материала состоит из трех основных разделов. В разделе «Прогнозирование и моделирование» рассмотрены основные концепции моделирования временных рядов и формализована задача прогнозирования как задача «вход-выход». Раздел «Подходы машинного обучения для моделирования временных зависимостей», посвящен обсуждению роли машинного обучения в создании точных предсказателей на основе наблюдаемых данных и знакомит с понятием локального обучения.

Прогнозирование и моделирование

Существуют две главные интерпретации задачи прогнозирования на основе исторических данных [9; 10]. Согласно теории статистического прогнозирования, наблюдаемая последовательность является одной из возможных реализаций случайного процесса, где случайность возникает из-за множества независимых степеней свободы, взаимодействующих линейно [5]. В то же время, теория динамических систем предлагает иную перспективу, предполагая, что кажущееся случайным поведение может быть результатом функционирования детерминированных систем с малым количеством степеней свободы, взаимодействующих нелинейно [8]. Такое сложное и нерегулярное поведение называется детерминированным хаосом.

Многие типы временных рядов, получаемых в экспериментальных данных, могут быть изучены с помощью теории динамических систем. В данном подходе временной ряд рассматривается как динамическая система, в которой состояние s ( t ) изменяется во времени в пространстве состояний Γ ⊂ Rⁿ по определенному закону:

s ( t ) = F t ( s (0)) ,                    (1)

где F : Г → Г – карта, представляющая динамику;

F^t – итерационное применение отображения F , то есть t -кратное последовательное применение F :

Ft (s (0)) = F (F (... F (s (0))...)), где функция F применяется t раз;

s (0) g Г - начальное состояние системы;

s ( t ) g Г - состояние системы в момент времени t ; t – целочисленный дискретный индекс времени.

Эта формула описывает эволюцию состояния системы во времени, где поведение системы полностью определяется динамическим правилом F и начальным состоянием s ( 0 ) .

В контексте анализа временных рядов наблюдаемое значение в момент времени t , как правило, не совпадает напрямую с внутренним состоянием s ( t ). Вместо этого наблюдаемое значение определяется функцией измерения G , которая связывает состояние системы с наблюдаемыми данными:

yt = G ( s ( t )) , (2) где G : Γ→ RD – функция измерения, которая отображает внутреннее состояние системы s ( t ) в наблюдаемую величину yt ;

D – размерность выходной наблюдаемой серии.

В данной статье рассматривается случай D = 1, то есть одномерный временной ряд.

Таким образом, функция G задает связь между состоянием системы s ( t ) и наблюдаемой величиной y t. Если G неизвестна, восстановление динамики системы на основании наблюдаемых данных становится нетривиальной задачей.

Формула (1) описывает, как состояние системы изменяется во времени в пространстве состояний Γ.

Формула (2) связывает внутреннее состояние системы s ( t ) с наблюдаемым значением yt через функцию измерения G .

Функции F и G неизвестны, поэтому в общем случае нельзя надеяться на восстановление состояния в его первоначальном виде. Однако имеется возможность воссоздать пространство состояний, которое в некотором смысле эквивалентно исходному.

Когда исследуют динамические системы, часто оказывается так, что важная информация о системе скрыта в наблюдаемых данных. Это особенно актуально, если непосредственный доступ к внутренним переменным системы отсутствует. Задача реконструкции пространства состояний решает проблему восстановления динамики неопределенной системы через те же наблюдаемые данные. Задача реконструкции пространства состояний состоит в восстановлении состояния, когда единственная доступная информация содержится в последовательности наблюдений yt. Основная идея заключается в использовании метода вложений (Embedding), предложенного Ф. Такенсом (Takens’ Theorem). Этот метод позволяет, используя лишь один временной ряд наблюдений, воссоздать фазовое пространство, эквивалентное исходному, следуя ключевым шагам: ( карта реконструкции ) Φ(s(t)):

Ф( S ( t )) =

= { g ( F - D ( s ( t )),..., G ( F ^{- 1} ( s ( t )), G ( s ( t )) } .

Это выражение можно записать через наблюдаемые значения временного ряда:

Ф( s(t)) = {yt - d,■■■ yt -1,yt}, где Φ : Γ→Rm – карта реконструкции, отображающая состояния системы в реконструированное фазовое пространство размерности m;

G – функция измерения, связанная с наблюдаемыми данными y ,

F^-k – обратное (временное) применение карты F , соответствующее состоянию системы на k -шагов назад;

d – временная задержка, определяющая шаг между элементами реконструированного вектора;

m – размерность реконструированного пространства (число используемых значений), называемая вложением или порядком. Согласно теореме Такенса, m >2 d , что гарантирует однозначное восстановление динамики системы;

t – индекс временного ряда, представляющий номер отсчета в дискретной последовательности { y_t }.

Основным следствием применения карты реконструкции Φ является то, что если Φ является вложением, то в пространстве восстановленных векторов индуцируется гладкая динамика f , задаваемая следующим уравнением:

y_t = f ( y_t - d ,y_t - d - 1 ,...,y_t - d - n + 1 ) . (3)

где f : Rⁿ → R – отображение, описывающее динамическую зависимость текущего наблюдения y_t от n-мерного вектора запаздывающих значений;

n – размерность реконструированного пространства, которая определяется количеством включенных задержек и должна быть достаточно большой ( n >2 dn ) для корректной реконструкции динамики;

d – шаг задержки (временной интервал между значениями в векторе). Это означает, что реконструированные состояния в пространстве Rn могут быть использованы для оценки функции f , которая описывает динамическое поведение временного ряда. Таким образом, f может выступать альтернативой исходным отображениям F и G для решения различных задач, включая качественное описание динамики, прогнозирование временных рядов и анализ их свойств.

Представление (3) не учитывает никакой шумовой компонент, поскольку оно предполагает, что детерминированный процесс f может точно описать временные ряды. Однако это просто один из возможных способов представления явления временного ряда, и любое альтернативное представление не должно быть отвергнуто априори. На самом деле, если предположить, что доступ к точной модели функции f нет, то вполне разумным решением будет расширить детерминистическую формулировку (3) до статистической нелинейной авторегрессионной формулировки (NAR).

y = f ( y - d , y - d - 1 ,..., y - d - n + 1 ) ⁺ w(f) , ⁽⁴⁾

где недостающая информация объединяется в шумовой член. В остальной части статьи мы будем ссылаться на формулировку (4) как на общее представление временного ряда, которое включает в себя в качестве частного случая также случай (3).

Успех подхода к реконструкции на основе набора наблюдаемых данных зависит от выбора гипотезы, которая аппроксимирует f , выбора порядка n и времени запаздывания d .

В следующем разделе будет рассмотрена проблема моделирования f , если предполагать, что значения n и d доступны априори.

Подходы машинного обучения для моделирования временных зависимостей

Обучение с учителем. Формулировка вложения в (4) указывает на то, что при наличии исторической последовательности S задача одношагового предсказания может быть решена как задача обучения с учителем. Обучение с учителем включает в себя создание модели, с опорой на множество наблюдений, которая устанавливает связь между входными переменными и одной или не- сколькими зависимыми выходными переменными. После того, как модель по отображению (4)

построена, ее можно применять для одношагового предсказания. В этом случае используются n предшествующих значений ряда, и задача предсказания представляется как обобщенная регрессионная задача, что показано на рисунке 1.

Общий подход к моделированию явления «вход/выход» со скалярным выходом и векторным входом основывается на наличии набора наблюдаемых пар, обычно называемых обучающим множеством.

При прогнозировании обучающее множество формируется на основании исторического ряда S путем создания матрицы [(N – n - 1) × n] входных данных:

y N - 1

X =

yn

yN - n y1

и выходного вектора [(N - n - 1) × 1]

yN

Y =

. yN + 1

Для простоты мы предполагаем здесь, что временная задержка d = 0, то есть значения векторов в матрице X берутся подряд без пропусков. В дальнейшем будем ссылаться на i-ый ряд матрицы X, который представляет собой запаздывающий вектор временного ряда – вектор состояния, описывающий n последовательных значений временного ряда. Этот вектор отражает состояние временного ряда в момент времени t - i + 1.

Инстанцирование с локальным обучением . Прогнозирование на шаг вперед заключается в предсказании значения выхода при заданном подмножестве прошлых наблюдаемых значений (также обозначаемом как запрос). Машинное обучение обеспечивает теоретическую основу для оценки по наблюдаемым данным подходящей модели временной зависимости f . Из-за невозможности рассмотреть здесь весь современный уровень машинного обучения в прогнозировании временных рядов, далее мы более конкретно рассмотрим методы локального обучения. Этот выбор обусловлен следующими причинами:

• 1.    Гибкость подхода . Локальные методы обучения не требуют строгих предположений о характере распределения данных или специфике процесса, лежащего в основе временного ряда. Это делает их пригодными для работы с реальными данными, которые часто имеют высокую степень нестационарности и шумности.

• 2.    Отсутствие необходимости в глобальной модели. Методы локального обучения не зависят от построения общей модели для описания всех данных. Вместо этого они используют только ближайшие данные для прогноза, что снижает риск переобучения на данных, содержащих выбросы или шум.

• 3.    Устойчивость к нестационарности. Локальное обучение эффективно работает с временными рядами, характеристики которых изменяются со временем. Методы легко адаптируются к новым условиям, что делает их особенно полезными для динамических и изменяющихся систем.

• 4.    Интерпретируемость. Результаты локальных методов, таких как метод ближайших соседей, могут быть легко интерпретированы, поскольку они основываются на сравнении с известными ранее наблюдениями.

• 5.    Возможность онлайн-обучения. Локальные методы обучения подходят для сценариев,

когда данные поступают в режиме реального времени. Такие методы позволяют обновлять обучающую выборку без необходимости полного переобучения модели, что снижает вычислительные затраты.

Локальное обучение не требует предварительных знаний о процессе, который лежит в основе данных. Например, оно не делает предположений о наличии общей функции, описывающей данные, и не имеет никакой связи со свойствами шума. Единственная доступная информация – это набор входных и выходных наблюдений. Эта особенность, главным образом важна для реальных данных, где проблемы отсутствующих характеристик, нестационарности и ошибок измерения делают подход, основанный на данных и свободный от предположений, особенно привлекательным.

Метод локального обучения легко справляется с задачами обучения в режиме онлайн, когда количество обучающих данных растет с течением времени. В таком случае локальное обучение просто добавляет новые точки в набор данных и не требует трудоемкого переобучения при появлении новых данных.

Метод локального обучения может работать с изменяющимися во времени конфигурациями, когда случайный процесс, лежащий в основе данных, является нестационарным. В таких случаях соседей целесообразно определять не только по пространству, но и по времени. Для каждой новой точки запроса соседями становятся не только те данные, которые имеют схожие входные параметры, но и те, которые были собраны недавно. Таким образом, временная переменная становится еще одной важной характеристикой, которую необходимо учитывать для точного прогнозирования.

В продолжение мы рассмотрим пример методов локального обучения: метод ближайших соседей и фрактальные методы анализа временных рядов.

Фрактальные методы анализа временных рядов. Помимо методов локального обучения, фрактальные методы анализа временных рядов предоставляют дополнительные возможности для изучения сложных динамических систем. Эти подходы фокусируются на выявлении самоподобия и масштабных закономерностей, что делает их особенно полезными в задачах прогнозирования и анализа временных данных.

Фрактальные методы анализа временных рядов являются мощным инструментом для исследования сложных динамических систем. Они позволяют выявлять скрытые структуры и закономерности в данных, которые часто не удается обнаружить с помощью традиционных методов. Фрактальные подходы основываются на концепции самоподобия, характеризующей временные ряды, и широко применяются в областях, таких как экономика, биология, геофизика и телекоммуникации.

Основные принципы фрактального анализа:

• 1.    Самоподобие временного ряда. Временной ряд считается фрактальным, если его структура остается неизменной при изменении масштаба времени. Это свойство описывается фрактальной размерностью D, которая может быть рассчитана через различные методы, такие как метод покрытия, метод ячеек или метод подсчета боксов (boxcounting).

• 2.    Гистограмма распределения шкал (Hurst Exponent). Экспонента Херста H является важной характеристикой фрактальных временных рядов. Она показывает степень долгосрочной памяти временного ряда:

• 3.    Фрактальная размерность по методу Кор-нфельда (также известная как корреляционная размерность). Для вычисления фрактальной размерности D₂ используется корреляционная сумма:

^R = ( NH ),

S где R – диапазон изменений временного ряда;

S – стандартное отклонение;

N – длина временного окна;

H ∈ [0,1] – экспонента Херста.

N Nn

C ( r ) =-------V V @( r - x - x

N (N -1) h.^fl (        j1), где C(r) – корреляционная сумма;

• r – радиус окрестности;

Θ – функция Хевисайда;

∥ x_i - x_j ∥ – расстояние между точками x_i и x_j . Размерность D₂ оценивается через наклон логарифмического графика зависимости C(r) от r :

log C ( r )

D 2 = lim--------.

• r ' ° log r

• 4.    Детрендированный флуктуационный анализ (DFA). DFA позволяет оценить сложность временного ряда, исключив влияние трендов. Основные этапы:

• 1 ) Разделить временной ряд на сегменты длиной n, для каждого сегмента вычислить локальный тренд методом наименьших квадратов, рассчитать флуктуации F(n) :

N

F(n ) = _ALЙ x ( i ) - T ( i )] ,

^N i = 1

где T(i) – локальный тренд, построить зависи- мость F(n) от n на логарифмическом графике.

Фрактальные методы позволяют:

• –    диагностировать наличие долгосрочных зависимостей в данных;

• –    выявлять масштабные структурные закономерности, что особенно полезно для сложных систем с многомерной динамикой;

  – анализировать свойства нестационарных временных рядов, часто встречающихся в финансовых и телекоммуникационных данных.

Ближайший сосед. Метод ближайшего соседа (Nearest Neighbors Algorithm, NN) – это самый простой пример локальной аппроксимации, который используется для прогнозирования временных рядов [11]. Суть метода в том, чтобы найти в наборе данных точку, ближайшую к текущему состоянию, и предположить, что текущее состояние будет развиваться аналогично найденному соседу.

На рисунке 1 представлен пример одношагового прогнозирования по ближайшим соседям. Предположим, что у нас имеется временной ряд y_t до момента времени t – 1, и мы хотим предсказать следующее значение ряда. После выбора определенной размерности n, например, n = 6, подход ближайшего соседа ищет шаблон в прошлом, который является наиболее похожим, в данной метрике, на модель { y_t-6 , y_t-5 , ... , y_t-1 } (пунктирная линия). Если ближайшим шаблоном является, например, { y_t-16 , y_{t -15} , ... , y_t-11 }, то прогнозы ŷ_t , возвращаемые методом NN, – это значение y_t-10 (черная точка).

Необходимо предсказать завтрашнюю погоду в Москве, имея временной ряд наблюдений. Предположим, размерность n = 1 (одномерный шаблон). Метод NN включает следующие шаги:

• 1.    Найти в исторических данных шаблон погоды, наиболее похожий на текущие условия. Например, это может быть погода 10 сентября 2020 года.

• 2.    Выбрать из данных погоду на следующий день после найденного шаблона (например, случайно дождливый день).

• 3.    Прогнозировать завтрашнюю погоду как значение, соответствующее следующему дню в историческом шаблоне.

Метод можно расширить, учитывая большее количество ближайших соседей или используя аппроксимацию более высокого порядка.

Таким образом, методы машинного обучения предоставляют мощные инструменты для решения задачи прогнозирования временных рядов, обеспечивая значительные преимущества по сравнению с традиционными статистическими подходами. В частности, методы локального об-

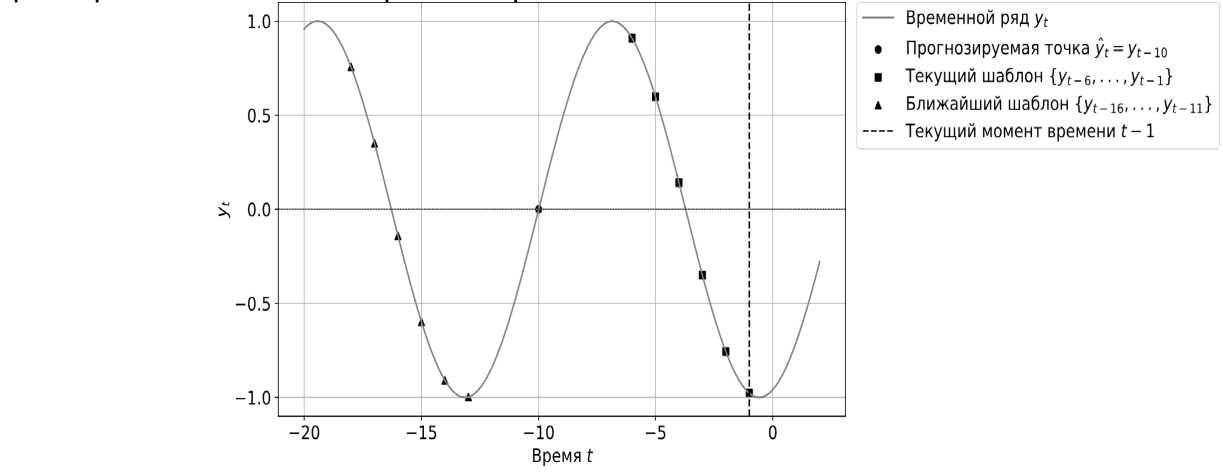
Рисунок 1. Пример одношагового прогнозирования методом ближайших соседей

учения, такие как ближайшие соседи и локальная регрессия, показывают свою эффективность в работе с реальными данными, где использование традиционных моделей может быть связано сс определенными ограничениями.

Заключение

В статье приведен подробный анализ применения методов машинного обучения для предсказания временных рядов, с выделением их основных преимуществ по сравнению с традиционными статистическими моделями. Установлено, что современные алгоритмы, включая искусственные нейронные сети, машины опорных векторов и регрессию ближайших соседей, демонстрируют более точные результаты при работе с нелинейными и сложными данными.

В статье проанализированы преимущества и ограничения как традиционных линейных методов (например, ARIMA), так и современных моделей машинного обучения. Показано, что последние, включая искусственные нейронные сети, обладают способностью учитывать сложные нелинейные зависимости, которые трудно моделировать с помощью классических методов.

Кроме того, выделены методы локального обучения, такие как метод ближайших соседей, фрактальные методы анализа временных рядов, а также описаны их преимущества: гибкость, способность работать с нестационарными данными и поддержка онлайн-обучения.

Рассмотрены основные трудности многошагового прогнозирования, такие как накопление ошибок и снижение точности при увеличении горизонта прогноза.

Важно подчеркнуть, что несмотря на заметное повышение степени точности предсказаний при использовании методов машинного обучения, выбор подходящего алгоритма и его параметров требует тщательной настройки в зависимости от специфики данных. Перспективные исследования должны быть направлены на оптимизацию существующих моделей, создание гибридных решений и дальнейшего распространения применения машинного обучения в анализе больших данных и для решения задач реального времени.