Использование методов математического моделирования для повышения эффективности настройки пороговых датчиков ускорения

В работе рассматривается проблема прогнозирования параметров настройки срабатывания порогового датчика ускорения (ПДУ). ПДУ используются в составе систем для коммутации электрических цепей при превышении действующим ускорением заданного порогового уровня. Наиболее близкими по функциональным параметрам к исследуемому прибору являются акселерометры прямого измерения. В отличие от рассматриваемого датчика ускорения в современных приборах используются иные физические явления [1, 2, 3] (акселерометры следующих типов: поплавковые, сухие с металлическим или кварцевым подвесом, электростатические, микромеханические). Описание акселерометров, конструктивно сходных с исследуемым, встречается в [4, 5]. Проблемы настройки рассматриваемого типа приборов в данных работах не анализируются, поэтому актуальной проблемой является получение аналитического описания влияния конструктивных параметров ПДУ на его функциональные характеристики.

Предметом исследования является ускорение срабатывания ПДУ и оценка влияния на него основных конструктивных параметров прибора: коэффициентов инерции, коэффициентов жесткости, шероховатости поверхностей, величины переносного ускорения, что определяет актуальность решаемой задачи.

В статье определяются величина переносного ускорения, при котором чувствительный элемент (инерционное тело) переходит из состояния относительного покоя к состоянию относительного движения, и закон дальнейшего движения по отношению к подвижной системе координат (корпусу прибора).

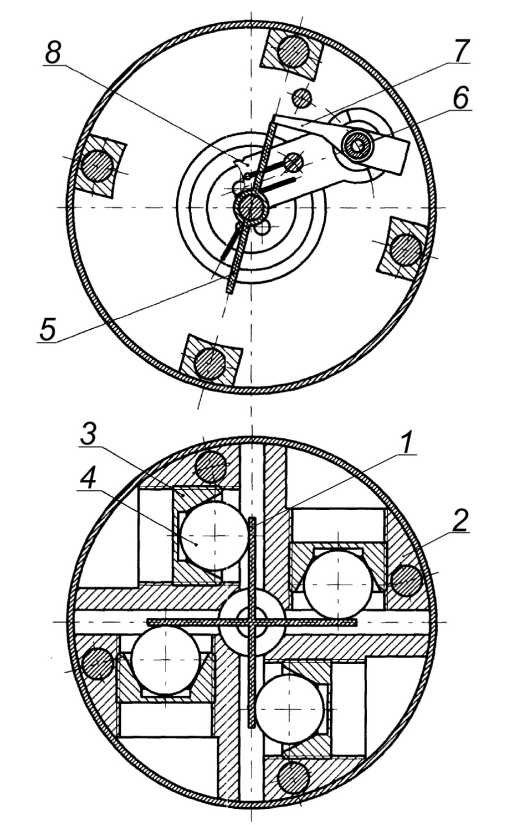
Рис. 1. Основные элементы конструкции порогового датчика: 1 — крестовина, 2 — корпус, 3 — конус, 4 —инерционное тело, 5 — фиксатор, 6 — вал, 7 — рычаг, 8 — перемыкатель

Анализируемый ПДУ имеет следующую конструкцию (рис. 1). Чувствительный элемент состоит из крестовины 1, установленной в корпусе 2 на двух шарикоподшипниках, и спиральной пружины, жестко закрепленной в корпус через обойму, четырех конусов 3 и четырех инерционных тел 4. Свободные осевые перемещения крестовины устраняются тарельчатой пружиной. Крестовина за счет усилия спиральной пружины поджимает инерционные тела к конусам. Механизм освобождения контактной системы состоит из фиксатора 5, установленного на крестовине 1 и удерживающего от поворота вал 6 через установленный на вал рычаг 7. Поворот вала обеспечивается спиральной пружиной. Контактная система состоит из перемыкате-ля 8, установленного на валу 6, и трех контактов.

Работа ПДУ осуществляется следующим образом: при действии ускорения в любом направлении инерционные тела 4 выкатываются из конусов 3 и поворачивают крестовину 1. Установленный на крестовине фиксатор 5 поворачивается, освобождая рычаг 7 и связанный с ним вал 6. Установленный на валу перемыкатель 8 замыкает требуемые контакты.

РАСЧЕТНАЯ СХЕМА

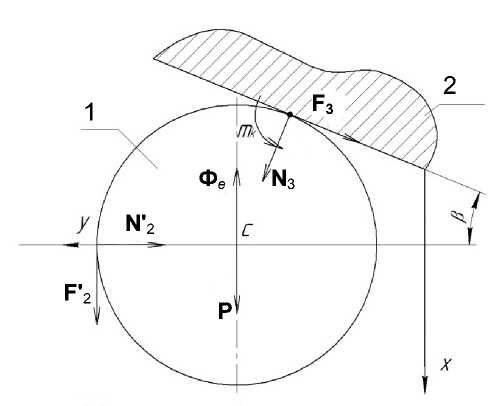
Расчетные схемы для момента отрыва приведены на рис. 2, 3. На расчетной схеме I: Р — сила тяжести; N' 2 , N 3 — нормальные составляющие реакции поверхности; F' 2 , F 3 — силы трения скольжения; m k — момент трения качения; Ф е — переносная сила инерции.

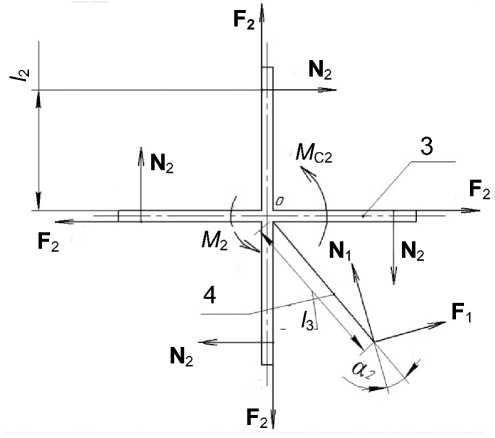
На схеме II: N 1 , N 2 — давление фиксатора и инерционного тела на крестовину; F 1 , F 2 — силы трения скольжения, выражаемые через нормальные реакции с помощью закона Кулона; М 2 — момент упругости спиральной пружины; М С2 — момент сопротивления в подшипниках.

МЕТОДИКА РАСЧЕТА

Установлено, что расчет можно разделить на две задачи: статическую и динамическую (относительное равновесие и относительное движение), что позволяет определить ускорение поступательно движущейся подвижной системы координат, при котором начинается движение инерционного тела.

I

II

Рис. 2. Расчетные схемы.

Расчетная схема I для момента отрыва:1 — инерционное тело, 2 — конус; расчетная схема II: 3 — крестовина, 4 — фиксатор механизма коммутации

Полученные результаты базируются на комплексном применении основных положений теоретической механики [6], математических методах анализа [7], а также натурном и математическом моделировании.

Вращательное движение крестовины 3 и плоское движение инерционного тела 1 (рис. 2) описываются дифференциальными уравнениями движения. Уравнения относительного покоя для определения величины [ a_e ] получаются из системы (1) - (4) при условии, что относительная скорость и ускорение равны нулю, при этом к действующим на тела силам добавлена переносная сила инерции.

В динамическом режиме работы уравнение движения для крестовины имеет вид

Ф 2 * J p = - M 2 ( Ф 2 ) - M C2 - N 1 * 1 3 sin а 2 -

— F * l3 cos а 2 + 4 * N2 * l2;

для инерционного тела:

Х * m = F 2 + P - K 1 * t * т ш - [ a e ] * т ш +

+ N3 cos в + F3sin в;(2)

Y * тш =-N2 + N3sinp - F3cosв;(3)

ф1 * Ju. =- F2 * r - mk + F3 * r, где mш , Jш , r — масса, момент инерции и радиус инерционного тела, Jкр — момент инерции крестовины.

Сила Ф„ имеет вид Ф„ = K. * t * т,„ + [ a, ] * m „,, где е е 1 ш еш

K ₁ — коэффициент нарастания ускорения. Решая систему (1) - (4) для обобщенной координаты ф₂, выполняя линеаризацию для малых значений параметров ( ф ₁ ~ 0 ° ...5 ° , ф₂ « 0 ° ...4 ° , Х ~ 0^1 мм, Y ≈ 0…0.6 мм) вблизи устойчивого положения равновесия, получаем уравнение второго порядка

Ф 2 + ( 0 0 * Ф 2 = D * K 1 * t + D * [ a e ] + E , (5)

где D , E — коэффициенты, полученные при алгебраических преобразованиях системы (1) - (4); ω ₀ — циклическая частота.

Общее решение уравнения (5) имеет вид:

Ф 2⁽ t ) =

= C₁₁ * cos( o ₀ 1 ) + C ₁₂ * sin( o ₀ 1 ) + H ₀₁ + H ₁₁ * t , (6)

где C ₁₁ , C ₁₂ — постоянные, определяемые из начальных условий. При значениях C ₁₁ = = 5.2 * 10^-5рад, C ₁₂ = 1.64 * 10^-5рад частное решение (5) представлено на рис. 3.

Задавая значения угла срабатывания, получаем время, соответствующее этому углу, и соответствующее ускорение срабатывания.

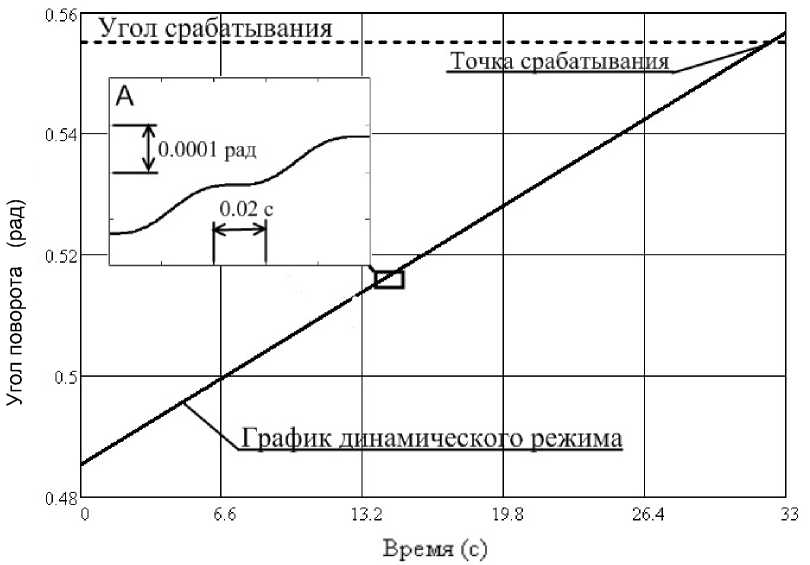
Рис. 3. График динамического режима ПДУ.

На фрагменте А показан в более крупном масштабе закон движения крестовины

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

• 1.    С помощью разработанной модели исследованы два варианта движения инерционного тела, определяющие получение требуемых функциональных характеристик: первый — качение без проскальзывания по конусу и проскальзывание по крестовине, второй — проскальзывание по конусу и качение без скольжения по крестовине. При качении инерционного тела без скольжения по поверхности конуса (нормальный режим работы) сила трения скольжения является неизвестной величиной, а при скольжении инерционного тела по крестовине — определяется с помощью закона Кулона. Соответственно для данного варианта кинематической схемы должно выполняться условие

• 2.    Параметры шероховатостей поверхностей конуса и крестовины влияют на ускорение срабатывания прибора за счет возникновения различных видов кинематических связей при движении инерционного тела по поверхности конуса и крестовины.

• 3.    При создании математического описания ПДУ использованы программы Ansys v. 12, Pro/ENGINEER Wildfire 3.0, с помощью которых а) проведен расчет зависимости момента, развиваемого плоской спиральной пружиной, от угла ее взведения (деформации пружины) при различных допусках на геометрические размеры; б) выполнен анализ влияния параметров закрепления концов спиральной пружины на момент упругости (см. таблицу); в) с помощью трехмерных моделей выполнен расчет моментов инерции и положение центра тяжести геометрически сложных элементов ПДУ, используемых при решении уравнений (1) - (4).

f 3 ≥ _N ^{F 3}₃ ,                     (7)

где f 3 — коэффициент трения скольжения.

Влияние параметров закрепления концов спиральной пружины на погрешность срабатывания ПДУ

Функциональная характеристика	Параметр
	l 1 — величина смещения пружины относительно вала в направлении стрелки	l 2 — величина смещения пружины относительно вала в направлении стрелки	l 3 — величина смещения пружины относительно вала в направлении стрелки
s g « q S g о и Ш Ш S3 в a s сз и й § о	Δ max = 0.8147 g	Δ max = 0.4541 g	Δ max = 0.0147 g

АНАЛИЗ

Для ПДУ проведенный анализ позволил определить степень влияния параметров начальной настройки на погрешность срабатывания при следующих значениях параметров, учитывая область значений ускорения срабатывания (25 g ≤ ≤ a_{сраб .} ≤ 30 g ) :

M 1 = 9.5∙10^–3 H·м — момент упругости, приложенный к рычагу;

M С1 = 0.4∙10^-3 H·м — момент трения в подшипниках рычага;

• α 2 = 0º;

• f 1 = 0.15 — - коэффициент трения кинематической пары (рычаг—фиксатор);

M 2 = 44.93∙10^–3 H·м — момент упругости, приложенный к крестовине;

M С2 = 0.4∙10^–3 Hм — момент трения в подшипниках крестовины;

k = 0.0015∙10^-2м — коэффициент трения качения пары (конус—инерционное тело);

• f 2 = 0.15 — коэффициент трения пары (поверхность крестовины—инерционное тело).

Области изменения параметров и соответствующие им погрешности батывания:

коэффициент трения f 2 пары (поверхность крестовины—инерци-онное тело)

коэффициент трения f 1 кинематической пары (рычаг—фиксатор)

угол α2 отклонения от 90º рычага к фиксатору начальный угол взведения пружины при определении ускорения сра- от 0.099 до 0.13, погрешность = 1.35 g;

от 0.099 до 0.13, погрешность = 0.134 g;

от 0 до 1.5 град, погрешность = 0.118 g;

от 27.323 до 30.032 град, погрешность = 2.31 g.

Согласно данным расчетам, можно сделать следующие выводы:

• - при большой жесткости спиральной пружины незначительные изменения угла взведения приводят к существенному изменению ускорения срабатывания;

• - максимальные изменения остальных технологических параметров приводят к изменениям погрешности срабатывания, значительно меньшим чем при изменениях угла взведения пружины.

Экспериментальное подтверждение разработанных математических описаний ПДУ проведено в процессе настройки партий выпускаемых датчиков в производственных условиях. В процессе работы было рассмотрено более ста ПДУ, накоплен значительный статистический материал. При настройке варьировались угол начального взведения плоской спиральной пружины, допуски на геометрические размеры и параметры шероховатостей контактирующих поверхностей. Коэффициент корреляции вектора данных, полученных экспериментальным путем, и вектора соответствующих расчетных данных составляет 0.966.

ВЫВОДЫ

• 1.    Полученные математические описания пороговых датчиков ускорения позволяют упростить

• 2.    Основным фактором, влияющим на начальную настройку порогового датчика, является начальный угол взведения плоской спиральной пружины, момент которой приложен непосредственно к крестовине. Все остальные факторы имеют меньшее влияние, их можно компенсировать корректировкой угла начальной деформации пружины.

процесс настройки путем выбора соответствующих параметров.