Использование методов прогнозирования для решения задач информационно-статистического анализа деятельности предприятия в условиях риска

Менеджменту предприятия любой организационно-правовой формы и сферы деятельности для определения конкретных перспектив развития предприятия необходимо уметь предвидеть его вероятное будущее, а также состояние среды, в которой оно действует. Многообразие проблем, возни кающих в процессах развития и являющихся предметом прогнозирования, приводит к появлению большого количества прогнозов, разрабатываемых на основе определенных методов прогнозирования, что требует формирования необходимой методической базы прогнозирования.

Известно, что все методы прогнозирования можно разделить на два больших класса: фактографические и экспертные.

Экспертные методы прогнозирования являются наиболее распространенными методами научно-технического прогнозирования. Они отражают индивидуальное суждение специалистов относительно перспектив развития объекта и основаны на мобилизации профессионального опыта и интуиции. Суждение о прогнозе возникает после соответствующей обработки ответов экспертов.

Экспертные методы прогнозирования используются для анализа объектов и проблем, развитие которых либо полностью, либо частично не поддается математической формализации, то есть для которых трудно разработать адекватную модель. Например, методы, основанные на экспертных оценках и заключениях, широко используются для оценивания риска инвестиционного решения в финансируемом проекте: вначале выделяются все негативные факторы, влияющие на возможное невыполнение проекта, а затем оценивается количественно их степень влияния и их объективная возможность проявления.

Заметим, что выбор экспертной группы является одним из наиболее важных и сложных вопросов. Эксперт должен удовлетворять следующим требованиям [2; 3]: оценки эксперта должны быть стабильны во времени, то есть не должны меняться в течение экспертизы без дополнительной информации; эксперт должен быть компетентным в данной области знаний, то есть должен быть признанным специалистом по исследуемым вопросам; оценка эксперта при наличии дополнительной информации может быть только улучшена.

Очевидно, что в практике проведения экспертиз всегда стремятся к минимально возможному числу экспертов в группе. В настоящее время нет достаточно обоснованной методики расчета необходимого числа экспертов в группе. Для расчета численности группы экспертов можно, например, воспользоваться известным соотношением математической статистики, которое используется обычно при вычислении погрешности на блюдений [2]: У\' =

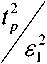
где N - число экспер-

Е тов в группе; ех=— - предельно допустимая относительная ошибка экспертной оценки, задаваемая из соображений точности; г- предельно допустимая величина абсолютной погрешности оценки; S - среднеквадратическое отклонение в распределении оценок какой-либо величины; t - коэффициент Стьюдента, определяющий ширину доверительного интервала и зависящий от величины вероятно сти оценки р.

В зависимости от заданной погрешности экспертной оценки и выбранной величины вероятности р может быть рассчитано минимально возможное количество экспертов в группе N.

Не менее важным вопросом, чем определение минимального объема экспертной группы, является оценка компетентности экспертов. Очевидно, что в зависимости от характера и вида продукции величина коэффициента компетентности у одного и того же эксперта может меняться и принимать значения от нуля (полностью некомпетентен) до единицы (наивысшее значение весового коэффициента).

Следует отметить, что в настоящее время объективные способы оценки экспертов практически труднореализуемы, и в основном используются достаточно субъективные способы - самооценка, взаимооценка и оценка на основании документов о квалификации.

В первом приближении можно оценить качество эксперта, используя формализованный подход к оценке его профессиональной компетентности [2].

Профессиональную компетентность, во-первых, определяют уровнем научной квалификации эксперта К, во-вторых, компетентность эксперта определяется структурой аргументов, послуживших ему основанием для оценки (коэффициент К), и степенью его знакомства с исследуемым вопросом (коэффициент К).

Степень влияния на мнение эксперта всех перечисленных источников аргументации

(К = 1 - высокая, К = 0,8 - средняя, К = 0,5 -низкая) определяется, как уже отмечалось, самим экспертом. Аналогично оценивается степень знакомства эксперта с проблемой.

Комплексный показатель компетентности z-ro эксперта можно вычислить по формуле К I К I к

К, _—к----а ----с [21 Величина К. лежит в

'              3

пределах от 0,05 до 1,0.

Стоит заметить, что, как правило, коэффициент профессиональной компетентности эксперта учитывается в виде множителя при соответствующей оценке, то есть служит коэффициентом значимости (весомости) мнения данного эксперта.

Показателями обобщенного мнения группы экспертов в этом случае являются показатели относительной важности определенного пункта: F -среднеарифметическое значение оценки у-го варианта (в баллах); f - частота максимально возможных оценок, получен-ныху-м вариантом.

Для вычисления среднеарифметического значения оценки может быть использована формула

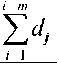
Wj где F - определяется для каждого варианта разработок; d - оценка относительной важности (в баллах), данная z-м экспертом у-му варианту (из 100 баллов); т - количество экспертов, оценивших у-й вариант.

Частота максимально возможных оценок, полученных у'-м направлением, вычисляется по зависимости fj =

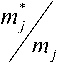
где т* - количе ство максимально возможных оценок, полу-ченныху-м вариантом разработок.

При принятии решения также важно учитывать, достаточно ли согласованы эти оценки, не является ли результат экспертизы усреднением диаметрально противоположных мнений.

Степень согласованности мнений экспертов может быть оценена с помощью коэффициента координации по формуле W = D / D^max

[2], где D - оценка дисперсии (разброса) мнений экспертов; D^max = ^т²(п³ - и) - максимально возможная величина дисперсии; у = 1,2,...,и - число факторов (вариантов), оцениваемых экспертами; 1 = 1,2,.. ,,т - число экспертов, участвовавших в оценке; d - оценка (баллы)у-го фактора (варианта) z-м экспертом.

Дисперсия достигает наибольшей величины (О = О™”) при полном совпадении мнений всех экспертов (присвоение одинаковых баллов, рангов, «коэффициентов весомости» и др.). Следует считать, что при W < 0,3 - согласованность экспертов плохая; при 0,3< W < 0,7- средняя; при W > 0,7 - высокая, W = 1 - полная согласованность мнений всех экспертов [2; 3].

Последовательность процедуры экспертного оценивания, например, функции риска, состоит из 4-х этапов, один из которых связан с вычислением степени влияния каждого из выбранных негативных факторов на получение желаемого дохода от проекта, полностью покрывающего кредитную задолженность.

Рассмотрим некоторую формальную модель расчета весовых коэффициентов [3]: пусть имеется п ранговых последовательностей R(j = 1,...щ), для которых может быть введена в рассмотрение одна из мер детализации учета соответствующих факторов по системе расчетных случаев Р (j = l,...,m):

А= max /?. - min /?.. (1)

Очевидно, что Д_у = max 7?,. -1, 1 < A_y<  m.

Заметим, что введение меры (1) не является однозначным. Степень детализации учета того или иного фактора может характеризовать и сумма рангов

8,=ТЛ (2) 1=1

и другие меры. Для рассмотрения данной схемы расчета выбор меры, как видно, не имеет принципиального значения. Если для рассматриваемых мер справедливо А, > А2 >...> А. >...> А„, то этим неравенствам можно поставить в соответствие простое отношение порядка предпочтения

В^В₂^...^В^...^В„. (3)

Символическая запись (3) означает, что первый фактор ранжирования расчетных случаев имеет больший ранг важности, чем второй, и т. д.

Количественную оценку степени предпочтения (3) дают так называемые оценки Фишборна

- 2(и-2+1) . ] 7      77(77 + 1)

И .

Очевидно, что эти оценки можно рассматривать в качестве весовых коэффициентов. Однако заметим, что для общего случая упорядочения ранговых последовательностей модели расчета весовых коэффициентов определяются следующим образом.

Пусть имеется и ранговых последовательностей R..(j = 1,...,и), характеризуемых мерой

Ау ^max/y -1. Пусть для рассматриваемых мер справедливо следующее соотношение:

^7-1 — ^1 ⁼ ^7+1 ⁼ ••• ⁼ ^j+k — ^7+t+l ’ (5) где к - степень кратности ранговых последовательностей при их упорядочении по мере А.

Тогда совокупности мер А. можно поставить в соответствие упорядоченную по степени предпочтения систему ранговых последовательностей

Д...в, -1) >- В^в^в^ ^- В^в_№у.

Такая символическая запись означает, что j, ;+1,... ,j+k факторы при ранжировании расчетных случаев имеют одинаковый ранг важности и больший, чем J+A+1 и т. д., и меньший, чем J-1 и т. д. Можно показать, что количественная оценка степени предпочтения (6), определяемая на основе использования принципа максимума неопределенности, имеет вид

» - У +1 А

где А = ^кДп - j +1) / = 7? -^kj -1). 7=1                             7=1

Можно заметить, что зависимость (7) является обобщением (модификацией) зависимости (4) и вырождается в нее при к = 1, j = 1,...,77.

Находим весовые коэффициенты [1]:

А2 = А4 = А5 = А15 = Alg = А20 = А31 = 1,

^8 = ^21 = ^23 = ^27 = ^32 = 2»

А3 = А6 = А? = Д9 = А10 = Ап = А12 =

= А13 = А14 = А16 = А17 = А19 = А22 =

= Д24 = Д25 = А26 = А33 = 3-му уровню значимости.

Следовательно, упорядочение ранговых последовательностей имеет следующий вид:

В₂(В₄,В₅,В_Ъ,В_Х%,В₂₀ , 5₃₁) >

> В_% (5₂₁, В ₂₃, 5₂₇, В₃₂) >

> В_х(В₃,B₆,B_n,В_Хй,В_и,В_Х2,В_Хз,В_Х4,В_Х6, В_Х1, В_Х9, В₂2, В₂₄, В₂₅ , S₂₆, S₂₈, S_2q,5₃₀, В33)

а сумма 5 определяется следующим образом:

5 = ^K>-j^,

7=1

где и = 33, К, = 7, К₂ = 5, К₃ = 21;

/ = w-^(^-1) = 33-[(7-1)+ (5-1) + (21-1)] = 3.

7=1

Таким образом 5 = 7(33 - 1 + 1) + 5(33 - 3 + 1) = =1042.

Тогда р - Р - Р - Р - р - р - р = '2    1 4    1 5    1 15    1 18    1 20

р = р = р = р = р = __ ^ + 1 = о 0307

Cl Сз С7 С2 1042+ р-р-р-р-р-р - р -р = 1 1    1 3    1 6    1 7     1 9    1 10 1 11

= Р - Р - Р - Р - Р - Р - Р - Р=

^П 1 16    1 17    210    1 77 1 7Д    1 75

= Р_7% = Р„ = Р₃„ = Р₃₃ =          = 0,0298.

Зная веса негативных событий (Р., j = = 1,...,33) и экспертные оценки вероятности каждого события (g., z = 1,2,3), функцию риска можно вычислить по формуле [4]:

3                               1 3

Rc =Y^j -Pj’ ^гД^е ^7

7=1                          -J /=1

В нашем случае суммарное значение риска R_c = 52,18. Но для того, чтобы оценка была более точной, необходимо вычислить доверительные интервалы, для этого вычислим дисперсию:

oi+j^E+л2.

7=1

где Р_к - вес к-го фактора (события);

В результате получим, что D[R(] ~ 13,76.

Тогда 38,42 <М[АС]< 65,94.

Заметим, что риск можно рассматривать как взвешенную по типовым частям проекта среднюю вероятность проявления негативных тенденций. Риск более 50 говорит о до статочно высокой степени проявления таких тенденций.

Таким образом, описание экономических процессов и решение экономических задач сегодня невозможно без использования методов системного анализа и прогнозирования. Они являются необходимым инструментарием менеджера-аналитика и активно используются в исследовательской практике организаций и предприятий различной направленности и структуры.