Использование методов стохастического программирования для моделирования таможенно-логистических каналов

Развитие интеграционных процессов в формате Евразийского экономического союза (далее – ЕАЭС) неизбежно оказывает влияние на осуществление внешнеэкономической деятельности (далее – ВЭД), и, в частности, в немалой степени воздействует на построение таможенно-логистических каналов.

В этой связи необходимо отметить существование противоречий в существующей системе таможенного регулирования и администрирования в рамках ЕАЭС. Так, несмотря на сближение (но еще не единство) подходов стран-членов ЕАЭС в области таможеннотарифного регулирования, между ними сохраняются существенные отличия в подходах к управлению рисками [2]. Различие в охвате системой управления рисками (далее – СУР) и жесткостью принимаемых мер по минимизации рисков, обуславливает наличие предпочтений участников ВЭД к осуществлению таможенных операций в том или ином государстве, входящем в ЕАЭС. Так, по свидетельству участников ВЭД, «жесткий фискальный характер» одного государства-члена ЕАЭС нередко вынуждает многих из них перестраивать логистические каналы с целью осуществления таможенных операций в таможенных органах иных государств-членов ЕАЭС [2]. При построении новой конфигурации логистического канала производится сопоставление затрат, вызываемых изменением маршрута, с затратами, связанными с избыточным, по мнению участников ВЭД, таможенным администрированием. Причем, данные затраты обладают неопределенным характером.

Т.о., предварительная рабочая задача на данном этапе может быть сформулирована следующим образом: нахождение минимального уровня затрат, связанных с перемещением

А.А. Дмитриев фирмой-перевозчиком товара через таможенную границу ЕАЭС, с учетом фактора неопределенности, при наличии возможности осуществлять таможенные операции в таможенных органах различных государств-членов ЕАЭС. Данная задача может быть решена методами стохастической оптимизации.

Перед формулировкой задачи в формализованном виде, введем следующие обозначения: x 1 и x 2 – количество товара, с которым осуществляются таможенные операции в таможенных органах государства-члена ЕАЭС №1 и ЕАЭС №2, соответственно, обе величины выражены в кг (вес брутто). T 1 и T 2 – удельное нормативное время осуществления таможенных операций с товарами в таможенных органах государства-члена ЕАЭС №1 и ЕАЭС №2, соответственно. Обе величины выражены в часах. Нормативное время определяется, исходя из нормативов перемещения товаров на определенное расстояние, и в общем случае являются предметом договоренности между фирмой-перевозчиком и заказчиком услуг по перевозке. В нормативном времени не учитывается время, затрачиваемое на временное хранение в соответствии с главой 25 ТК ТС.

На данном этапе следует отметить некоторые вычислительные трудности, возникающие при определении удельной величины времени, затрачиваемого при перемещении 1-го кг товара. На самом деле, временные затраты при увеличении количества перемещаемого товара возрастают скачкообразно, как примерно показано на рис.1.

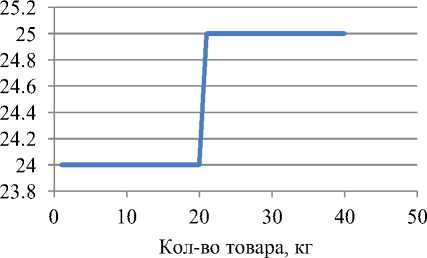
Рисунок 1 – Модель перемещения товара на двух прицепах

На рис. 1 показан график ступенчатой функции. График моделирует ситуацию перемещения товара в 2-х прицепах седельного тягача грузоподъемностью 20 т. Каждое транспортное средство полностью загружено. Общее нормативное перемещение первого прицепа составляет 24 часа. Если вслед за ним отправляется второй полностью загруженный прицеп с такой же грузоподъемностью, то общее нор- мативное время увеличится на час – приращение времени обусловлено интервалом между грузовиками, различием дорожных условий и другими факторами. Очевидно, что увеличение количества товара в пределах вместимости грузовика не вызывает линейного роста временных затрат – ведь на время пути грузовика существенно не повлияет, сколько товара в него загружено – 1 тонна или 20 тонн. Но для решения поставленной задачи необходимо найти значение коэффициента, выражающего линейную зависимость между количеством товара и временными затратами. С этой целью необходимо будет осуществить аппроксимацию ступенчатой функции [4]. Решение этой вспомогательной задачи выходит за рамки данной статьи, и может быть рассмотрено в отдельной работе.

M 1 = F 1 – Т 1 и M 2 = F 2 – Т 2 – превышение удельного фактического времени (F₁ и F₂) осуществления таможенных операций над удельными нормативными временными затратами в таможенных органах государства-члена ЕЭАС № 1 и 2, соответственно. Все величины выражены в часах.

Превышение может быть обусловлено:

• -    функционированием СУР. В частности, таможенный досмотр может увеличить время перемещения товара в диапазоне от 3 часов до 9-ти суток.

• -    нарушением пропускной способности пунктов пропусков на государственной границе.

Обозначим с 1 и с 2 – стандартные издержки, связанные с превышением удельного фактического времени осуществления таможенных операций над удельными нормативными временными затратами в таможенных органах государства-члена ЕЭАС № 1 и 2, соответственно. Выражаются в рублях за 1 час.

Издержки вычисляются, в частности, как расходы на временное хранение товара вследствие применения СУР, а также как упущенная выгода от несвоевременного поступления товара на прилавки магазинов. В отношении упущенной выгоды стоит отметить, что хоть заказчики и не штрафуют перевозчиков за задержки, обусловленные таможенным администрированием, впоследствии эти издержки снижают цену на услуги по перевозке, и штраф за задержку накладывается на перевозчика косвенно.

Не все партии товаров «простаивают» на границе. Выразим долю товаров, фактическое время перемещения которых через таможенную границу превышает нормативное, в общей доле товаров, как P1 и P2, для государст- ва-члена ЕАЭС № 1 и № 2, соответственно. Допустим, эти доли характеризуют вероятности сверхнормативной задержки на таможенной границе.

Величина превышения фактического времени над нормативным временем также носит случайный характер. Поэтому для корректного выражения удельных (то есть в расчете за 1 кг брутто веса товара) издержек превышения (M 1 с 1 и M 2 с 2 ) автор предлагает использовать математическое ожидание удельных издержек превышения:

nnn

E(c 1 M 1 )=с 1 P 1 ∑ pM 1 ,             (1)

n где p – вероятности того, что величина пре- 1

вышения примет соответствующие значения n

M ₁ , где верхний индекс n отражает количество 1

значений, которые принимает M 1 .

Аналогично для государства-члена ЕАЭС №2:

nnn

E(c 2 M 2 )=с 2 P 2 ∑ pM 2            (2)

Пусть f 1 и f 2 – удельные нормативные издержки доставки товара (транспортировка, перегрузка и т.д.) с пересечением таможенной границы государств-членов ЕАЭС № 1 и № 2, соответственно. Издержки фирмы-перевозчика могут быть получены расчетным путем по данным учета расходов организации. Если же вычисляются расходы транспортно-экспедиторской компании, то для расчета удельных издержек могут быть использованы коммерческие предложения фирм-перевозчиков. К примеру, предложение Shenker устанавливает тарифы на доставку для сочетаний диапазонов расстояний и диапазонов количества товара. В таком случае для получения линейного коэффициента затрат по перевозке 1 кг товара, возможно потребуется построить ступенчатую функцию с последующей аппроксимацией.

Примем с 1 и с 2 – предельно допустимые суммы нормативных затрат на доставку товара с пересечением таможенной границы государств-членов ЕАЭС № 1 и № 2, соответственно.

Сформулируем исходную задачу в формализованном виде [2]:

E(c1 M1)x1 + E(c2 M2)x2 -> min;(3)

P [f1 x1≤ C1] ≥ β1;(4)

P [f2 x2≤ C2] ≥ β2.(5)

Выражения (4) и (5) представляют собой вероятностные ограничения, и могут быть сформулированы следующим образом: «общие нормативные издержки перемещения товара не должны превысить предельно допустимой суммы С 1 иС 2 с вероятностью, не меньшей β 1 и β₂, соответственно».

Рассмотрим применение метода на конкретном примере. Для этого используем условные данные, представленные в таблице 1.

В соответствии с условными данными в указанной выше таблице запишем целевую функцию и вероятностные ограничения [2]:

1530 x1+312 x2 ^ min;(6)

P [24 x1≤ C1] ≥ β1;(7)

P [85 x2≤ C2] ≥ β2.(8)

Определим для вероятностных ограничений (7) и (8) их детерминистические эквиваленты [2]:

24 x1≤ В1;(9)

85 x2≤ В2.

Используя безусловное распределение величины С из таблицы 1 (строки 8 и 9), определим значения В 1 и В 2 . С этой целью сначала определим зависимость P[C≤B] от B 1 [2]. Зависимость представлена на следующем графике (рис. 2), где: В 1 = 160000 рублей при условии, что 0,8 ˂ β 1 ≤ 1,0, В 1 = 200000 рублей при условии, что 0,2 ˂ β 1 ≤ 0,8, В 1 = 250000 рублей при условии, что 0 ˂ β 1 ≤ 0,2.

i,o

0,8

160        200      250

Bl (в тыс.рублей)

Рисунок 2 – Зависимость P[C≤B] от B 1

Аналогично, В 2 = 540000 рублей при условии, что 0,8 ˂ β 2 ≤ 1,0, В 2 = 600000 рублей при условии, что 0,2 ˂ β 2 ≤ 0,8, В 2 = 670000 рублей при условии, что 0 ˂ β 2 ≤ 0,2.

Условимся, что ограничения затрат будут иметь значение при 0,2 ˂ β 1 ≤ 0,8 и 0,2 ˂ β 2 ≤ 0,8. Тогда с учетом изменений в правой части

А.А. Дмитриев

(9) и (10), задачу оптимизации можно переписать в виде [2]: 1530 x 1 +312 x 2 -> min;               (11) 24 x 1 ≥ 200000;                       (12) 85 x 2 ≥ 600000 .                         (13) Решим ее с помощью симпекс-метода. Опуская подробности расчетов, выводим результат: Сверхнормативные затраты будут минимальны при x 1 = 8333, x 2 = 7059.

Таким образом, несмотря на то, что удельные сверхнормативные расходы при транспортировке по Маршруту 1 значительно выше по сравнению с Маршрутом 2, по Маршруту 1 можно отправить большую часть груза. В то же время это превышение обусловлено тем, что ограничения на совокупные нормативные расходы для Маршрута 2 (выражение (13)) в три раза превышают аналогичную величину для Маршрута 1 (выражение (12)).

Таблица 1 – Сведения для расчета логистических издержек

№ п	Исходные данные	Условные обозначения исходных данных	Маршрут 1 (через таможенную границу Белоруссии и Польши)			Маршрут 1 (через таможенную границу Казахстана и Китая)
1	Удельное нормативное время осуществления таможенных операций, в час	Т	4			3
2	Значения превышения удельного фактического времени осуществления таможенных операций над удельными нормативными временными затратами (Удельное время простоя)	M	8	25	36	2	10	22
3	Вероятности соответствующих значений M	p	0,1	0,7	0,2	0,1	0,8	0,1
4	Вероятность "простоя на таможенной границе"	P	0,3			0,2
5	Издержки "простоя на таможенной границе", рублей в час	c	200			150
6	Величина удельных издержек "простоя на границе" - рублей за 1 кг веса брутто товара	E(cM) = (8*0,1+25*0,7+ 36*0,2)*0,3*20 00	1530			312
7	Удельные нормативные издержки доставки товара (транспортировка, перегрузка и т.д.) с пересечением таможенной границы, рубл за кг	f	24			85
8	Предельно допустимая сумма нормативных затрат на доставку товара, в рублях	C	160000	200000	250000	540000	600000	670000
9	Вероятность соответствующих значений спроса	P c	0,2	0,6	0,2	0,2	0,6	0,2

А значения удельных сверхнормативных затрат влияют на минимальную величину сверхнормативных издержек.

Таким образом, в соответствии с приведенным выше подходом можно определить, как различия в подходах к таможенному администрированию, реализуемому таможенными органами различных государств-членов ЕАЭС, существенным образом влияют на общую величину сверхнормативных логистических издержек. Осталось найти ответ на вопрос о том, как влияет величина удельных сверхнормативных издержек на целесообразность выбора того или иного маршрута.

Для этого переформулируем исходную задачу следующим образом [1]:

x 1 + x 2 -> max; (14) 1530 x 1 ≤ 3000000; (15) 312 x 2 ≤ 3000000. (16)

В этой задаче на максимизацию коэффициенты при ограничениях (15) и (16) взяты из таблицы 1 и выражают величину удельных сверхнормативных расходов, а константы в правых частях ограничений – величину активов, резервируемых на покрытие сверхнормативных затрат. Мы опустили здесь подробности преобразования вероятностных ограничений в их детерминистический эквивалент.

Решением будут значения переменных: x 1 = 1961 и x 2 = 9615. Таким образом, более выгодным будет перемещение товара по Маршруту 2 – через территорию государства-члена ЕАЭС, в котором СУР издержки, связанные с таможенным администрированием, не столь обременительны для участников ВЭД.

Подводя итоги, можно отметить следующее:

• -    Издержки, связанные с таможенным администрированием товаров, перемещаемых через таможенную границу ЕАЭС, существенно различаются у государств-членов ЕАЭС, и носят неопределенный характер. Для корректной оценки этих издержек целесообразно использовать вероятностные характеристики, такие как математическое ожидание;

• -    Для расчета оптимальной величины расходов на доставку и распределения количества товара, перемещаемого через территорию различных государств-членов ЕАЭС, допустимо использование стохастических оптимизаци-

• онных моделей. В том числе возможно использование моделей с вероятностными ограничениями.

• -    Требуется дальнейшая проработка вопроса о корректном аналитическом представлении зависимости транспортных расходов от количества товара и расстояния, на которое перемещаются товары. Как вариант - построение ступенчатой функции с возможностью последующего сглаживания. Решение это вопроса необходимо для адекватной оценки удельных расходов по доставке, используемых в моделях оптимизации;

• -    Практическое использование стохастических оптимизационных методов при моделировании процессов таможенно-логистического сервиса возможно только при наличии эффективной автоматизированной системы сбора и обработки информации о сроках перемещения товаров через таможенную границу. В свою очередь программные средства, позволяющие оценить оптимальные показатели таможенной логистики, целесообразно интегрировать со средствами сбора информации, и уже в рамках данного контура, по мере обновления информации о временных и иных затратах, автоматически корректировать оценки оптимальных значений.

Все эти факторы в совокупности предопределяют дальнейшие пути теоретических и практических разработок в области оптимизации таможенно-логистического сервиса.