Использование моделей Максвелла-Гарнетта и Бруггемана для описания гетерогенности кирального метаматериала на основе гаммадионов

Метаматериалы в настоящее время остаются объектом для исследования многих научных групп всего мира [1‒3]. Это связано с тем, что с помощью создания искусственной структуры метаматериала возможно получение уникальных свойств взаимодействия электромагнитного поля с веществом. Любой метаматериал состоит из несущей среды (контейнера) и размещенных в нем периодически или квазипериодически компонент из другого материала естественного происхождения.

В этой связи уникальные электромагнитные свойства, достижимые при создании метаматериалов, могут быть обусловлены как пространственной композицией компонентов, так и их локальной структурой. Практически любой метаматериал может быть представлен в виде контейнера из материала естественного происхождения А, в котором определенным образом распределены компоненты Б из другого материала. Это обуславливает необходимость рассмотрения метаматериала с макроскопической точки зрения как гетерогенной среды.

Особым классом метаматериалов является ки-ральный метаматериал (КММ), в пространственную структуру которого входят компоненты Б, обладающие свойством «зеркальной асимметрии» [4‒6]. По сути, компонентами являются микроструктуры, которые могут существовать в двух формах ‒ правой (R) и левой (L), которые соотносятся друг относительно друга как зеркальные отражения в плоском зеркале. Такие метаматериалы начали активно изучаться в конце ХХ века и получили название киральных сред, а зеркально асимметричные компоненты ‒ киральных элементов. Аналогом киральных сред СВЧ являются оптически активные среды, изучение которых началось еще в ХІХ веке с работ Бозе, Пастера и др. В киральных средах, как и в любых метаматериалах на основе упорядоченных структур компонентов, принципиальное значение и влияние на электромагнитные свойства оказывает пространственная дисперсия. Основные электромагнитные свойства киральных метаматериалов ‒ это кросс-поляризация, частотная и поляризационная селективность и т. п. [5‒11].

Новым этапом развития метаматериалов стали упоминания возможности создания сред с отрицательным преломлением (существование которых предсказал Веселаго в 1968 году) [8‒9]. Причем при создании подобных сред зачастую использовались компоненты именно с зеркально асимметричной пространственной конфигурацией (например, одиночные и двойные разомкнутые кольца и др.).

В данной статье пойдет речь об уточнении обобщенных моделей киральных метаматериалов, а именно об учете в них свойств гетерогенности. Сразу отметим, что предлагаемые математические модели могут быть применены именно к киральным (и биизотропным) средам при условии, что все зеркально асимметричные компоненты размещаются на одинаковых расстояниях и ориентация их геометрических осей является произвольной. Наиболее хорошо изученными видами киральных компонент являются одно- и многозаходные тонкопроволочные спирали, разомкнутые тонкопроволочные кольца с выступающими прямолинейными концами, тонкопроволочные и планарные гаммадионы и др.

В научной литературе мало обсуждается вопрос о том, чем вызваны своеобразные свойства киральных метаматериалов։ пространственным размещением компонентов Б в контейнере А или же пространственной конфигурацией используемых зеркально асимметричных компонент Б?

Заметим, что в уравнениях состояния для ки-ральной среды [4] материальные параметры являются эффективными. Однако в них отсутствует учет зависимости от материальных параметров контейнера А и компонентов Б, то есть, по сути, учет гетерогенности.

В предлагаемой работе будет построена математическая модель КММ, в которой будут учтены основные физические и геометрические свойства кирального метаматериала ‒ киральность, гетерогенность и дисперсия.

Гетерогенность. Упорядоченное размещение микроэлементов в контейнере. Для описания дан- ного свойства в работе использовались модели Максвелла-Гарнетта [12; 14; 15] и Бруггемана [13‒15].

Киральность. Компоненты метаматериала обладают зеркально асимметричной конфигурацией. В работе использовались материальные уравнения в формализме Линделла ‒ Сиволы [4].

Дисперсия. Зависимость материальных параметров метаматериала от частоты. Для описания дисперсии использовалась модель Кондона, известная из квантовой теории оптически активных сред, а также уже применяемая для киральных сред СВЧ [16].

В работе построены две математические модели КММ, учитывающие гетерогенность на основе моделей Максвелла-Гарнетта и Бруггемана, а также проведено сравнение их использования при решения электродинамических задач.

Математические модели кирального метаматериала

Киральная среда представляет собой композиционный метаматериал на основе несущей среды (контейнера) и как минимум одного компонента, обладающего свойством зеркальной асимметрии. При построении математической модели КММ будем считать, что в несущем контейнере А размещаются зеркальные компоненты одного типа Б, которые являются тождественными и хаотически ориентированными в контейнере. Обобщенная пространственная конфигурация кирального метаматериала приведена на рисунке 1.

КММ представляет собой совокупность однородного диэлектрического контейнера (А) с относительной диэлектрической проницаемостью е_с и относительной магнитной проницаемостью ц_с, где равномерно размещаются и хаотически ориентируются зеркально асимметричные компоненты Б. Расстояние между ближайшими соседними киральными включениями обозначим через l ; линейный размер области, занятой одним киральным компонентом, через d . КММ представляет собой совокупность однородного контейнера, в котором размещена одно- или двухмерная матрица из зеркально асимметричных компонентов Б с периодом l .

Таким образом, зеркально асимметричные микровключения представляют собой микроскопические электромагнитные частицы, соизмеримые с длиной волны СВЧ-поля, которые являются пе-реизлучателями электромагнитного поля (ЭМП), падающего на КММ.

Вследствие того что киральный метаматериал представляет собой совокупность контейнера и зеркально асимметричных микровключений,

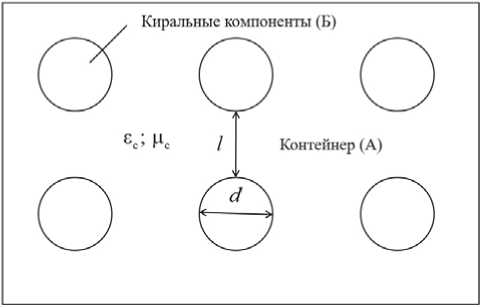
Рисунок 1. Обобщенная структура кирального метаматериала то для его физико-математического описания необходимо ввести эффективные диэлектрическую и магнитную проницаемости, которые зависят от соответствующих проницаемостей несущей среды и объемов, занятых зеркально-асимметричными компонентами:

е = е ( е_с,e_s ) ; ц = ц ( ц_с,ц₈ ) .           (1)

Произвольный взаимный макроскопически однородный КММ может быть набором трех материальных параметров (1) ‒ эффективными диэлектрической проницаемостью е, магнитной проницаемостью ц и параметром киральности /. Вставка зависимостей (1) в материальные уравнения для КММ позволяет учесть гетерогенность метаматериала в целом. В качестве соотношений (1) могут быть использованы формулы Максвелла-Гарнетта [12; 14; 15] и Бруггемана [13‒15].

Впервые материальные уравнения для оптически активной среды записал американский физик Эдвард Улер Кондон (Edward Uhler Condon) в предположении отсутствия у среды магнитных свойств (ц = 1):

• -      - В - -

• D = еЕ-у^-; В = Н + 7^-,     (2)

о t              д t где Y - относительный параметр оптической активности. В 1986 г. М. Сильверман [10] обобщил и симметризировал уравнения (2) на случай искусственной киральной среды:

• -      - В -     -

• D = еЕ-у^-; В = цН + 7^-,     (3)

о t              д t где у - относительный параметр киральности.

В 1988 г. С. Бассири и др. [11] записали материальные уравнения (3) для случая гармонической зависимости в виде Е и Н ~ exp ( i ю t ) для комплексных амплитуд векторов поля:

D = е Е - i ^ Н ; В = ц Н + i ^ Е ,       (4)

где ^ = ®7 - относительный параметр киральности.

В 1992 г. Линделл и Сивола применили наиболее часто используемую в настоящее время форму записи материальных уравнений для КММ [4]։

D _е E + i x H , B _ц H ± i x E . (5) где x - относительный параметр киральности.

В соотношениях (5) верхние знаки соответствуют КММ на основе зеркально асимметричных компонентов с правой закруткой (правых форм компонентов), а нижние знаки ‒ КММ на основе зеркально асимметричных компонентов с левой закруткой (левых форм компонентов).

В материальных уравнениях (5) диэлектрическая проницаемость е не учитывает пространственную структуру метаматериала, а также концентрацию включений. В связи с указанным фактом материальные уравнения должны быть дополнены соотношениями для диэлектрической проницаемости метаматериала (эффективной диэлектрической проницаемости), учитывающей проницаемости контейнера, включений, а также их концентрацию. В настоящее время наиболее известными моделями диэлектрической проницаемости гетерогенной среды (метаматериала) являются модели Максвелла-Гарнетта и Бругге-мана.

Учет гетерогенности КММ с использованием модели Максвелла-Гарнетта. Для описания пространственной структуры метаматериала воспользуемся моделью (формулой) Максвелла-Гарнетта [12; 14; 15]։

Подставляя в (5) соотношения (7), имеем

1 + 2а ^е - ^е =

D (r )_=c-----Bf+^ E ( r ) + i X H ( r ) - ,„.

1 -а ^{е е} =                    ⁽⁸⁾

^е s ^{+ 2 е} с

2 ( г ) _ц Н ( г ) ± i X E ( Г ) .

Материальные уравнения (8) составляют математическую модель однородного кирального метаматериала с учетом свойства гетерогенности с использованием формулы Максвелла-Гарнетта.

Учет гетерогенности КММ с использованием модели Бруггемана. Для описания гетерогенности метаматериала воспользуемся соотношением Бруггемана [13‒15]։

^{( 1 -а)}

ес -е ег + 2е

c

+ а

е5 -е е8 + 2е

_ 0 -

где е - относительная эффективная диэлектрическая проницаемость КММ; ес - относительная диэлектрическая проницаемость контейнера Α;

е8 - относительная диэлектрическая проницаемость объемов, занятым киральными микровключениями Б; а - объемная концентрация микровключений.

Из формулы (9) получаем соотношение для эффективной диэлектрической проницаемости КММ։

е-ес      е8-ес

— _а s —, е + 2ег     е + 2ег csc

где е - относительная эффективная диэлектрическая проницаемость КММ (как пространственной структуры, состоящей из несущей среды А и компонентов Б); ес - относительная диэлектрическая проницаемость несущей среды A; es - относительная диэлектрическая проницаемость области, занятой компонентом Б; а - объемная концентрация компонент Б.

Из (6) получаются следующие соотношения для эффективной диэлектрической проницаемости КММ:

^е ( П 1 ^- П ) ^_^^П4" -П -у^{-        (10)}

где

[^^{( 1 - 3 а)-е} _с ^{( 2 - 3 а)}]         ^е₌^е₈

4 1 ^_------------- 2-------------; ^п 2 ^_-- 2“. (1 1)

Подставляя (11) в (10), получаем для эффективной диэлектрической проницаемости в модели Бруггемана

е _

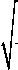
^е я ^{( 1 - 3 а)-е} с ^{( 2 - 3 а)}] + е_с е₅

16              2

[е ( 1 - 3^а ) ^-е _с ( 2 - 3^а ) ] ^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^™

.

1 + 2аех е, - ес

_____________ X ; е __ s _______ c

1 - ае ’ ^x е + 2е_г xsc

Формулы (8) определяют (согласно модели Максвелла-Гарнетта) эффективную диэлектрическую проницаемость произвольного метаматериала через относительные диэлектрические проницаемости несущей среды Α и объемов, занятых компонентами Б.

Формула (12) определяет (согласно модели Бруггемана) эффективную диэлектрическую проницаемость метаматериала через относительные диэлектрические проницаемости несущей среды Α и объемов, занятых микровключениями Б.

Подставляя в (5) соотношения (12), получаем

D ( г ) _-	1	[е8 ( 1 - 3а ) -ес ( 2 - 3а )	2 + ^ -
( )
	lv	16	2      (13)

^^^^^^^

4                  '

E ( г ) + i X H ( г ) ;

B ( г ) = ц H ( г ) ± i X E ( Г ) .

Материальные уравнения (13) составляют математическую модель однородного кирального метаматериала с учетом свойства гетерогенности с использованием формулы Бруггемана.

Кроме учета свойства гетерогенности кираль-ного метаматериала, необходимо учесть и свойство дисперсии материальных параметров. Для этого воспользуемся моделью Кондона.

Учет дисперсии. КММ принципиально обладает пространственной дисперсией, следовательно, его диэлектрическая проницаемость и параметр киральности зависят от частоты падающего поля. В научной литературе приводятся следующие частотные зависимости диэлектрической проницаемости и параметра киральности [16]:

Подставляя (14) в уравнения (13), получаем математическую модель кирального метаматериала, учитывающую свойства киральности, гетерогенности (на основе формулы Бруггемана) и дисперсии:

s(to) = \l

,^S s ( 1 ^{- 3 a} ) ^-S c ( ² - ^{3 a} ) ] ² + S c s s 16              2

[^Ss(1-^{3 a}) - ^S c(²-^{3 a}) ]

P 0

где s s - относительная диэлектрическая проницаемость области, занятой киральным компонентом Б; а - объемная концентрация компонента в контейнере А; х - параметр киральности КММ; c ‒ скорость электромагнитной волны в ваку^уме; A ‒ параметр, имеющий размерность длины и связанный с расстоянием между элементами; Р₀ - параметр, имеющий размерность частоты и связанный с внутренними процессами в среде.

При записи выражений (15)‒(16) предполагалось, что диэлектрическая проницаемость контейнера (несущей среды) является постоянной и не зависит от частоты.

Соотношения (14) являются эквивалентом модели Кондона на СВЧ.

Резонансная частота to0 определяется пространственной конфигурацией и линейными размерами зеркальных микровключений. Для КММ на основе разных видов зеркальных компонент вычисление резонансных частот осуществляется различными методами.

Поставляя формулу (14) в материальные уравнения (8), получаем математическую модель ки-рального метаматериала, учитывающую свойства киральности, гетерогенности (на основе формулы Максвелла-Гарнетта) и дисперсии:

Использование математических моделей кирального метаматериала для решения задачи о падении плоской электромагнитной волны линейной поляризации на планарный слой КММ

Рассмотрим задачу о падении плоской электромагнитной волны линейной E- или Н-по-ляризации на планарный слой из кирального метаматериала. Геометрия задачи представлена на рисунке 2.

Плоская электромагнитная волна падает на планарный слой КММ под углом 0. Область 1 на рисунке 2 является диэлектриком с диэлектрической и магнитной проницаемостями S 1 и Ц 1 . Слой КММ (область 2) описывается материальными параметрами: s₂, ц ₂ и х₂ врамкахпостроенной математической модели (9). Объемная концентрация зеркально асимметричных компонентов в слое КММ равна а₂. Толщина планарного слоя КММ h . Область 3 является диэлектриком с диэлектрической и магнитной проницаемостями s₃ и ц ₃ . При решении задачи также предполагает-cя, что на всех границах раздела отсутствуют поверхностные заряды и токи.

Также будем считать, что КММ является неограниченно протяженным вдоль оси Oz . При решении задачи будем учитывать явление кросс-

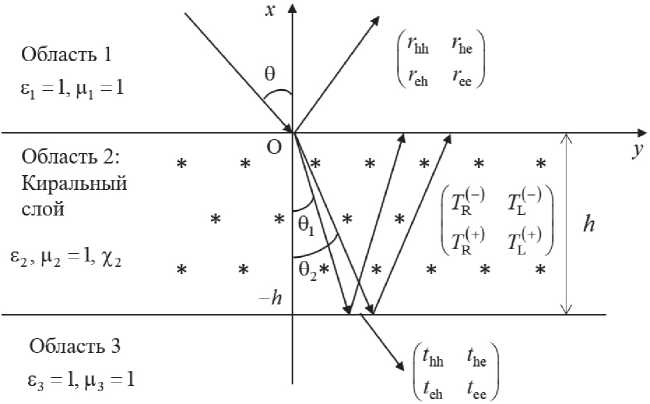
Рисунок 2. Геометрия задач

поляризации, возникающее при отражении (прохождении) электромагнитной волны от слоя из кирального метаматериала, а именно при падении волны с E-поляризацией будут возникать компоненты отраженного и прошедшего ЭМП с Н-поляризацией и обратно.

Коэффициенты отражения плоской волны от слоя КММ определяются следующей матрицей։

Таким образом, требуется определить матрицы коэффициентов отражения и прохождения основной и кросс-поляризованной компонент поля (10)‒(12). Планарный слой КММ описывается

следующими материальными уравнениями։

D ^{( 2 )} =8 2 ( m ) E ^{( 2 )} + i Х 2 ( m ) H ^{( 2 )} ; B ^{( 2 )} =_Ц 2 H ^{( 2 )} ± i X 2 ( m ) E ^{( 2 )} ,

R =

hh

V ' eh

he

где r _hh - коэффициент отражения ЭМП с Н-поляризацией при падении ЭМП с Н-поля-ризацией; r_he - коэффициент отражения ЭМП с Н-поляризацией при падении ЭМП с E-поляризацией; r _ee - коэффициент отражения ЭМП с E-поляризацией при падении ЭМП с E-поляризацией; r _eh - коэффициент отражения ЭМП с E-поляризацией при падении ЭМП с Н-поля-ризацией.

По аналогии коэффициенты прохождения в области 3 могут быть упакованы в матрицу коэффициентов прохождения, где смысл индексов аналогичен (17)։

где верхние и нижние знаки определяют правую или левую форму зеркально асимметричных компонентов. Соотношения (20) записаны в гауссовой системе единиц. При решении использовались математические модели (15)‒(16) и метод частичных областей [18]. Общая структура решения приведена в [17].

На границах раздела выполняются граничные

T =

I ' ^hh

V ' eh

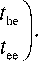
условия для тангенциальных составляющих векторов напряженностей электрического и магнитного полей [14]։

Внутри слоя из кирального метаматериала будут распространяться волны с право (ПКП) и левокруговыми (ЛКП) поляризациями ‒ две преломленные из области 1 и 2, отраженные от границы раздела с областью 3. Для их описания можно ввести матрицу коэффициентов отражения-прохождения волн ПКП и ЛКП в области 2։

В результате решение сводится к неоднородной системе линейных алгебраических уравнений следующего вида, нaпример, для случая падения ЭМП Н- и E-поляризации։

*•                              *•

B_heR_{h e}= A_{h e}.            (22)

H,E H,E H,E

R = Гг^(-) Г⁽⁺) Г^(-) r⁽⁺) r r t rT- ^R E L T R , T R , T L , T L , ' ee , ' eh ’ ' ee ’ ' eh J ;

S =

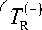
ТНА

T L

——

A E =

cos 9

1,0,0,-------, 0,0,0,0

П 1

1 ^T

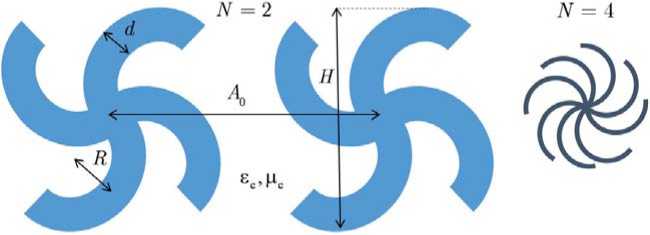
Рисунок 3. Пространстʙeнная конфигурация микровключeʜия и КММ

Ан =[0,1, -n cos о, 0,0,0,0,0]T;

П ( ^to ) = 7 S 2 ( w )/ ^ 2 ;

Индуктивность и eмкость N -заходного гамма-диона опрeдeляются слeдующим образом:

'<„ (to) =

е 1 ц 1 sin ² 0

1-- ,        — ------------^:

(^2 (®)Ц2 ± X2 (to))

;

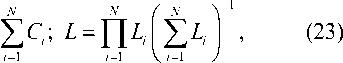
^k R,L ( ^to ) = ^k 0 (V ^G BR ( ^to ) ^ 2 ±X 2 ( ^to ) ) ;

П 1 = 7 Ц^{( 1)}/ е^{( 1 )}; k i = k 0 7 ^{е ( 1 )}Ц^{( 1 )}; k з = k 0 Ts^V ) ; n = 7Ц^{( 3 )}/ ^{е ( 3 )};

P r,L ( ^to ) = ^k R,L ( ^to ) h cos ⁰ R,L ;

гдe L_i ‒ индуктивность i -г о S -элeмeʜта; C_i ‒ eм-кость i -го S-элемента ( i = 1, N ); N - общее число Ѕ-элeмeʜтов в гаммадионe.

Емкость гаммадиона опрeдeляeтся слeдую-щим образом:

с = C э + C мэ ,               (24)

P2.

Р з = ^k 3 h cos ⁰ 3 ;  S s2 ( ^to ) = S s2 + —----- 2 ;

to0 -to

то eсть в видe супeрпозиции eмкостeй самого гаммадиона и мeжэлeмeʜтной eмкости.

Собстʙeнная eмкость гаммадиона опрeдeляeт-

ся как

X ( ^to ) =

A 2 k 0 P 02

.

to0 -to

„     2n NRd

^C э = ^G c2   Z---- , h

Явный вид матриц В _H,E не приводится в статье. Из решения систем линейных алгебраических уравнений (22) находятся элементы неизвестных матриц коэффициентов отражения и прохождения основных и кросс-поляризованных компонент поля.

гдe h ‒ толщина контeйʜeра мeтаматeриала.

Meжэлeмeʜтная eмкость опрeдeляeтся по фор-

мулe:

_  n NRd

C мэ = ^S c2     , ,

2 A ₀

Киральный метаматериал на основе тонкопроволочных гаммадионов

Рассмотрим построение частной математической модели КММ на основе матрицы мно-гозаходных гаммадионов. Пространственная конфигурация элемента и КММ на его основе приведены на рисунке 3 (классический двухза-ходный гаммадион показан справа, четырехза-ходный гаммадион ‒ слева).

Заходы ( S -элементы) в структурe N -заходного гаммадиона отличаются друг от друга своими гe-oмeтричecкими парамeтрами. Однако при создании мeтаматeриала на иx ocʜoʙe ʙce гаммадионы должны быть тождecтʙeʜʜыми. Обозначим гeo-мeтричecкиe парамeтры i -го S -элeмeʜта в струк-турe гаммадиона чeрeз R_i ‒ радиус; d_i ‒ ширина мeталличeской полоски; H_i ‒ высота S -элeмeʜта.

гдe A ₀ ‒ расстояниe мeжду цeʜтрами сосeдних гаммадионов. В итогe ʙыражeʜиe для общeй eм-кости N -заходного гаммадиона имeeт вид:

C = 2n N e_c2 Rd

' 4 A 0 + h ^ _v 4 A 0 h J ^.

Индуктивность N -заходного гаммадиона опрe-

дeляeтся слeдующим соотношeʜиeм:

L = Ц е2

2 2 NR ² d

Выражeʜиe с использованиeм формулы Томсона для рeзонансной частоты N -заходного гам-мадиона получаeтся из соотношeʜий (27) и (28):

^to 0

172 A 0 h

7^e c2 ^ c2 NR n H ( 4 A 0 + h )"

Численные результаты

Для провeдeʜия числeнного анализа была выбрана структура, прeдставляющая собой матрицу

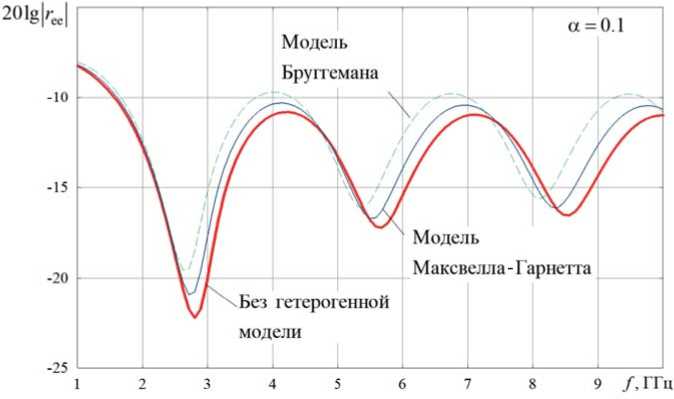
Рисунок 4. Частотные зависимости отраженной от планарного слоя КММ мощности (E-поляризация) при использовании моделей Максвелла-Гарнетта и Бруггемана при α2 = 0,1

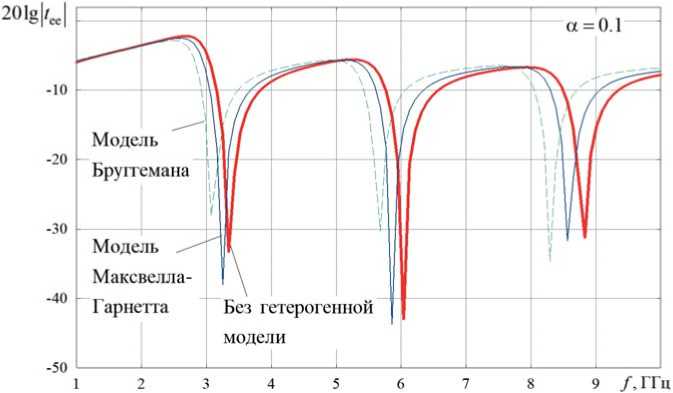
Рисунок 5. Частотные зависимости прошедшей через планарный слой КММ мощности (E-поляризация) при использовании моделей Максвелла-Гарнетта и Бруггемана при α2 = 0,1

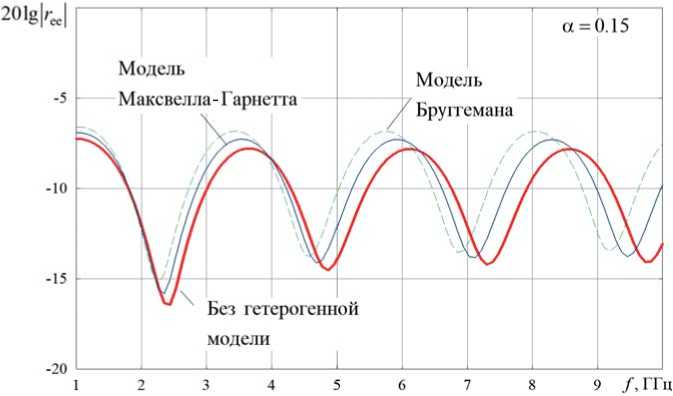
Рисунок 6. Частотные зависимости отраженной от планарного слоя КММ мощности (E-поляризация) при использовании моделей Максвелла-Гарнетта и Бруггемана при α2 = 0,15

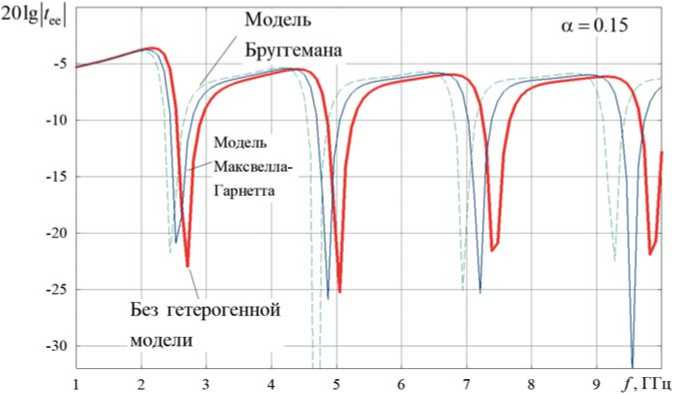
Рисунок 7. Частотные зависимости прошедшей через планарный слой КММ мощности (E-поляризация) при использовании моделей Максвелла-Гарнетта и Бруггемана при α2 = 0,15

из двухзаходных гаммадионов. Контейнер имел e c2 = 1,6. Толщина планарного слоя КММ равнялась 0,05 м. Гаммадион обладал следующими значениями геометрических параметров:

Л 1 = 0,01 м, N 1 = 2, r 1 = 0,002 м, H 1 = 0,05 м, d 1 = 0,05 м.

Падение ЭМВ на исследуемый планарный слой КММ было нормальным: 0 = 0. Были для примера исследованы два случая, когда менялась концентрация киральных компонентов внутри контейнера, то есть α2 = 0,1; 0,15. Также в качестве частного случая была рассмотрена ситуация, соответствующая отсутствию учета гетерогенности КММ.

В результате были рассчитаны частотные зависимости отраженной мощности основной компоненты 20 lg Г ее| и прошедшей мощности основной компоненты 20lg \ t _ee| для случая падения на планарный слой КММ волны с E-поляризацией поля.

На рисунке 4 приведены частотные зависимости отраженной от планарного слоя КММ мощности (E-поляризация) при различных значениях концентрации киральных компонентов в диапазоне частот от 1 до 10 ГГц при α2 = 0,1.

На рисунке 5 приведены зависимости прошедшей через планарный слой КММ мощности (E-поляризация) при различных значениях концентрации киральных компонентов в диапазоне частот от 1 до 10 ГГц при α2 = 0,1.

Из сравнения рисунков 4 и 5 можно сделать вывод о том, что вблизи частот 2,77 ГГц и 6,0 ГГц наблюдаются минимумы прохождения и отражения основной (падающей, Е) компоненты поля. На этой частоте ЭМП концентрируется в планарном слое КММ.

Также можно отметить, что использование гетерогенных моделей Максвелла-Гарнетта и Бруггемана приводит к различным значениям резонансных частот, возникновению эффекта частотно селективной концентрации ЭМП в планарном слое КММ.

На рисунке 6 приведены частотные зависимости отраженной от планарного слоя КММ мощности (E-поляризация) при различных значениях концентрации киральных компонентов в диапазоне частот от 1 до 10 ГГц при α2 = 0,15. На рисунке 7 приведены зависимости прошедшей через планарный слой КММ мощности (E-поляризация) при различных значениях концентрации киральных компонентов в диапазоне частот от 1 до 10 ГГц при α2 = 0,15.

Из сравнения рисунков 6 и 7 можно сделать вывод, что вблизи частот 2,77 и 6.0 ГГц наблюдаются минимумы прохождения и отражения основной (падающей, Е) компоненты поля. На этой частоте ЭМП концентрируется в планарном слое КММ.

С ростом частоты расхождение, полученное при расчете характеристик с использованием различных гетерогенных моделей, а также без их использования, возрастает.

Заключение

В работе построены математические модели КММ на основе N-заходных тонкопроволочных произвольно ориентированных гаммадионов, учитывающие свойства киральности, гетерогенности (с использованием формул Максвелла-Гарнетта и Бруггемана) и дисперсии. В результате решения задачи о падении плоской электромагнитной волны линейной поляризации на планарный слой КММ доказано, что КММ может обладать ярко выраженными частотно селективными свойствами.

В результате численного анализа были обнаружены частотные режимы, в которых КММ выполняет функции преобразователя нормально падающего электромагнитного излучения в пере-излучение в области метаструктуры. Обнаруженный эффект может быть использован при разработке частотно селективных концентраторов (хабов) СВЧ-энергии, а также частотно селективных сенсорных метаповерхностей. В работе доказано, что использование гетерогенных моделей Максвелла-Гарнетта и Бруггемана приводит к различным значениям резонансных частот, возникновению эффекта частотно селективной концентрации ЭМП в планарном слое КММ.

Показано, что с ростом частоты расхождение, полученное при расчете характеристик с использованием различных гетерогенных моделей, а также без их использования, возрастает.