Использование моделей упругого основания для анализа распределения локальных напряжений в стенке стальных составных балок

Подкрановые пути одноэтажных производственных зданий представляют собой сложную систему конструктивных элементов, воспринимающих подвижные нагрузки от мостовых кранов. Основным несущим элементом этой системы являются подкрановые балки, эксплуатационная надежность которых в первую очередь зависит от уровня локальных напряжений в верхней зоне стенки, определяющих ее усталостную прочность и долговечность.

Конструктивная форма подкрановых балок – составные двутавры, которые до середины 50-х годов прошлого века изготавливались под краны тяжелых режимов работы с использованием клепаных поясных соединений (рис. 1, а, б).Для таких балок характерна многоэлементность верхней зоны стенки. Известно [1], что при эксплуатации заклепочные поясные соединения проходят через три стадии работы под нагрузкой, обусловленной их податливостью. Отмеченные конструктивные и технологические факторы клепаных балок обеспе-чиваютих высокую усталостную долговечность.

В сварных балках, как видно из рис. 1, в, отсутствует многоэлементность верхней зоны. Поэтому единственным регулятором местного на- пряженного состояния стенки сварной балки и поясного шва является крановый рельс. Неслучайно отечественная металлургическая промышленность приступила к прокатке специальных крановых рельсов типа КР(ГОСТ 4121–48) в 50-е годы прошлого века при массовом переходе от клепаных балок к сварным [2]. В клепаных балках для перемещения колес мостовых кранов достаточно было использовать брусковые крановые рельсы.

Однако для обеспечения усталостной прочности верхней зоны стенки сварных балок применения специальных крановых рельсов оказалось недостаточным и потребовалось введение между рельсом и поясом балки прокладки из материала с низким модулем упругости [3]. Это позволило значительно снизить местные напряжения сжатия σ _loc,y и изгиба σ f _,y в стенке балки за счет распределения сосредоточенного давления колеса крана на бóльшую длину стенки (рис. 2, а) и поворота рельса на прокладке (рис. 2, б). Подрельсовые низкомодульные подкладки позволяют также ликвидировать неблагоприятное влияние на усталостную прочность стенки неровностей на контактных поверхностях подошвы рельса и верхнего пояса [4].

Согласно [5], деформативность клепаного по-

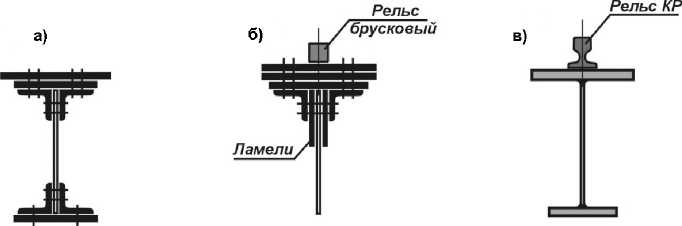
Рис. 1. Типы сечений подкрановых балок: а – сечение клёпаной балки; б – верхняя зона стенки балки с ламелями; в – сечение сварной подкрановой балки

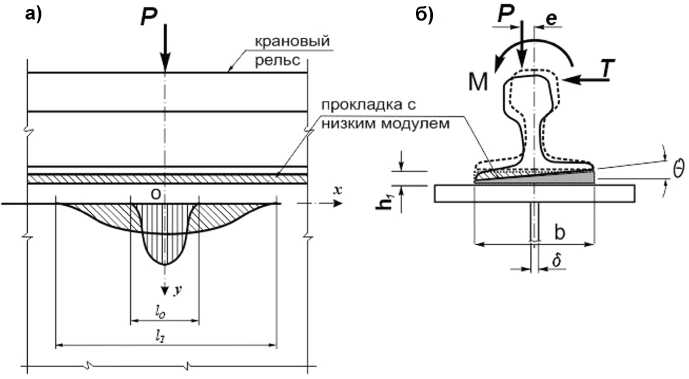
Рис. 2. Распределение напряжений о _1ос ^ в стенке балки (а) и деформация рельса на прокладке при действии локального момента (б)

ясного соединения стенки определяется коэффициентом податливости k = G₃ ( п d2aa ) , где d и а - соответственно диаметр и шаг заклепок в верхней зоне стенки; G _з = (0,8…2,0)·10⁶ кг/см²– модуль сдвига заклепочного соединения [1]. Для изготовления балок наиболее часто использовали заклепки диаметром d= 22 мм и шагом а = 100 мм.

При данных входных параметрах коэффициент податливости k изменяется в диапазоне (0,7…0,28)·10⁶ кг/см² в зависимости от стадии работы заклепочного соединения. Для вывода расчетной формулы l_e f в [5] коэффициент податливости принят равным k = 0,3·10⁶ кг/см², что соответствует работе соединений в балках, эксплуатируемых длительное время. Следовательно, поясное соединение на дискретных связях (в данном случае заклепках) также представляет собой некоторую область стенки с низким модулем упругости по сравнению с материалом стенки.

Эффективность различных конструктивных решений поясных соединений в подкрановых балках сводится к изучению напряженно-деформированного состояния упругого основания, на которое опирается крановый рельс, загруженный локальными воздействиями колес крана. В случае использования низкомодульной прокладки в сварных балках или наличия податливой зоны в балках с дискретными поясными соединениями стенку балки можно представить в виде двухслойного упругого основания (рис. 3), в котором слой h ₁ моделирует прокладку или податливое поясное соединение, а слой h ₂ – упругую полуплоскость (стенку балки). Каждый слой имеет свои упругие константы – модуль упругости и коэффициент Пуассона E 1 , V 1 и E ₂, v ₂ соответственно (рис. 3).

Задача о распределении напряжений σ loc,y в стенке балки при однослойном упругом основании рассмотрена в [6] и показала хорошую сходимость с экспериментальными данными.

Рассматриваемая задача представляет собой плоскую задачу теории упругости в перемещениях, связь между напряжениями и деформациями в которой выражается зависимостями:

°х = 2^ (ех + Ve у);

° у = TE2 (е у +Ve х ) ;

E

Т ху = 2(1+v) Y ху,

где v - коэффициент Пуассона; е _х = —; е y = —; д х       д у

( д и д v )

Y х , у = I        ⁺ I ■

^д у д х )

Основываясь на физическом смысле задачи, считаем, что в упругих основаниях h1 и h2 гори- зонтальные перемещения u отсутствуют, u (x, у ) = 0 .

Тогда система уравнений (1) примет вид:

E   (д v )

т. е.

^{Т ху} 2 ( 1 + v ) (д х ) •

Перемещения произвольной точки упругой полуплоскости будут происходить только в направлении оси y и примут вид:

^v ( ^х , у ) = V I ( у ) v i ( у ) ⁺ V 2 ( у ) v 2 ( у ) ,     ⁽³⁾

где Vi (у) и v2 (у) — функции распределения перемещений по высоте упругих слоев; V1 (у) и V2 (у) - вертикальные перемещения поверхности упругого слоя h1 и h2 соответственно (рис. 3, а).

Выбор функций распределения перемещений по высоте упругого слоя зависит от мощности это-

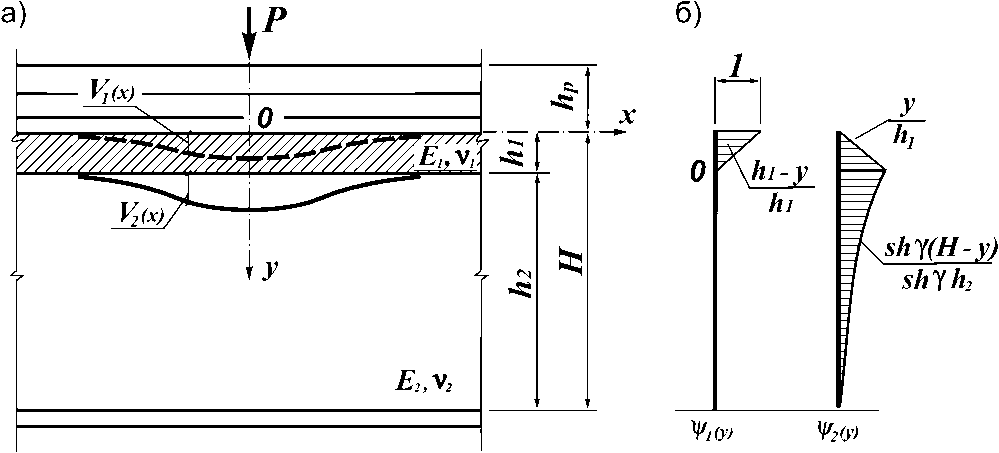
Рис. 3. Расчетная схема стенки балки как двухслойного упругого основания

го слоя, а также от характера распределения напряжений по высоте. Так, для слоя h ₁ , работающего на сжатие и имеющего небольшую высоту по сравнению с h ₂ , можно принять, что перемещения

изменяются по закону:

V i ( У ) = ⁽ h i ^- У )/ h i •

Функция V2 (У) для второго слоя может быть принята в виде [6]:

shY( H - у)

V 2 ( У ) =--------- ,                          (5)

sh y h 2

что соответствует физическому содержанию задачи и подтверждается экспериментами. Коэффициент y в формуле (5) характеризует затухание пе-

ремещений по высоте слоя h ₂ и равен γ = 0,25–

0,30 [7].

где E ‘ = E i Ь - относительный модуль податливости первого слоя, b – ширина подошвы рельса; δ – толщина упругой полуплоскости.

Коэффициенты k ₁ и k ₂ характеризуют соответственно работу верхнего и нижнего слоев на сжатие, коэффициенты t ₁ и t ₂ – на сдвиг.

Для решения системы дифференциальных уравнений (7) введем новую функцию F ( x ) и выразим через эту функцию и ее производные искомые перемещения V_i ( x ) и V ₂ ( x ) так, чтобы второе уравнение системы (7) удовлетворялось тождественно при любом выборе функции F ( x ) . Исходя из этого получим

V i ( x ) = ( k i + k 2 ) F ( x ) - 2 ( t i + 1 2 ) F' ' xx ) ;

V 2 ( x ) = k _i F ( x ) + t _i F' ‘ ( x ) .

Таким образом, функции распределения пе-

ремещений по высоте слоев будут иметь следующие значения (рис. 3, б)

0 <  у <  h ; V i = h^y ; V 2 = y- ; ¹                h ₁                 h ₁

sh Y ( H - у )

hi < у < H; Vi = 0; V2 = shYh 2

Используя выражения (4) и (6) и на основании решения, полученного в [7], будем иметь систему двух дифференциальных уравнений

2 t_iV { '- k V + t _i V 2 + k_iV 2 + q = 0;      ]

2 tV ‘+ kV + 2 ( t _i + t ₂ ) V 2 - ( k_i + k ₂ ) V 2 = 0,⁽⁷⁾

где k _i =

E 5

k ₂

h i ( ^{i -v} i2 )

E ₂ 5

.    ₌ E h i 5   .

; ⁱ = i2 ( i + v i ) ;

^h 2 ( ^{i -v 2} )

Eh 5

V k ^; 1 2 =     2 J \ V t ^;

ⁱ² ( ^{i + v} 2 )

_ y H sh Y H ch Y H - y H

• ^V k = ~7            Tj ^;

• 2 sh y H

= 3 i shYH chYH -yH t 2 yH     sh2yH     '

Подставив формулы (11) в (7), убеждаемся, что второе уравнение обращается в тождество, а первое примет вид tx (3tx + 412) FIV - 2 (3tikx + txk2 +12kx) F'‘ +

+ k , k 2 F = q ( x ) , (i2) где q ( x ) - нагрузка на упругое основание.

Дифференциальным уравнением (12) полностью описывается напряженное и деформированное состояние двухслойного упругого основания. Выбирая характеристики k ₁ , k ₂ , t ₁ , t ₂ можно получить ряд различных расчетных схем упругого основания и рассматривать эффективность подрельсовых устройств, выполненных из разных материалов и имеющих различные конструктивные исполнения.

Для отыскания неизвестной функции перемещения F ( x ) , удовлетворяющей дифференциальному уравнению (12) и конкретным граничным условиям, примем несколько предпосылок:

• i.    Осадка верхнего слоя V , ( x ) равна прогибу кранового рельса, лежащего на этом основании.

• 2.    Ввиду малой толщины слоя й_г верхний слой работает только на сжатие и представляет

• 3.    Деформации первого и второго слоев происходят в упругой области работы материала этих оснований.

собой винклеровское упругое основание. Для такого слоя можно принять

1 1 = 0; k i = k o ,                                (13)

где k ₀ –коэффициент постели упругого основания h ₁ .

С учетом (13) уравнения системы (11) примут

вид

^V 2 ( x ) = k 0 ^F ( x ) , а дифференциальное уравнение (12) перепишется при этом в виде

- 2 k ₀ 1 ₂ F " + k ₂ k 0 F = q ( x ) .                 (15)

Дифференциальное уравнение (15) позволяет рассмотреть работу двухслойного упругого основания с верхним винклеровским слоем.

Для балки, лежащей на винклеровском упругом основании, дифференциальное уравнение изогнутой оси имеет вид:

EIV₁ ^IV ( x ) = p ( x ) - q ( x ) , (16)

где V - упругий прогиб балки; p (x) - нагрузка на балку; q (x) - нагрузка на основание (реактивное давление).

Вследствие того, что прогиб балки по условию нашей задачи совпадает с осадкой поверхности упругого слоя основания V1 , первое из уравнений системы (14) может быть внесено в выражении (16). Для определения основной функции F (x) получим при этом систему двух дифферен- циальных уравнений:

EI [- 2 1 2 F^V + ( k о + k 2 ) F IV ] = p ( x ) - q ( x ) ; ' - 2 k 0 1 ₂ F " + k₂ k , ₀ F = q ( x ) .

неизвестную функцию q ( x ) , для чего сложим почленно первое и второе уравнение и получим выражение

• - 2 EI -2- F V + Ei ^k0U^kL F IV —

k ₀              k ₀

p ( x )

• -2 1₂F " + k₂P = ^A                 (18)

k 0

которое является основным уравнением задачи и представляет собой обыкновенное дифференциальное уравнение шестого порядка с постоянными коэффициентами.

Рассмотрим бесконечно длинную балку на упругом основании, подчиняющемся гипотезе Винклера, и загруженную сосредоточенной силой Р . Исходя из предпосылки 1, прогиб балки и вертикальные перемещения поверхности упругого слоя к _г одинаковы и равны [8]:

y ( x ) = V ₁ ( x ) = в е. e ^{e x} (cos p x + sin P x )], (19)

где в = 4 k₀-bj 4 EI – упругая характеристика основания; k ₀ – коэффициент постели упругого основания; b – ширина подошвы рельса; ЕI – жесткость рельса на изгиб. Эпюра прогиба бесконечно длинной балки, загруженной сосредоточенной силой, представлена на рис. 4, а.

Для балок с низкомодульной прокладкой коэффициент постели упругого основания может быть представлен в виде k ₀ = E ₁ /h₁ . Таким образом, верхний слой с упругими характеристиками E ₁ и v ₁ преобразован в упругий слой, свойства которого характеризует коэффициент k ₀ .

Для выявления закономерностей распределения местных напряжений в стенке рассмотрим задачу о распределении давления под подошвой рельса или в уровне поясных заклепок (болтов) стенки. Для винклеровского основания давление

Исключим из полученной системы уравнений

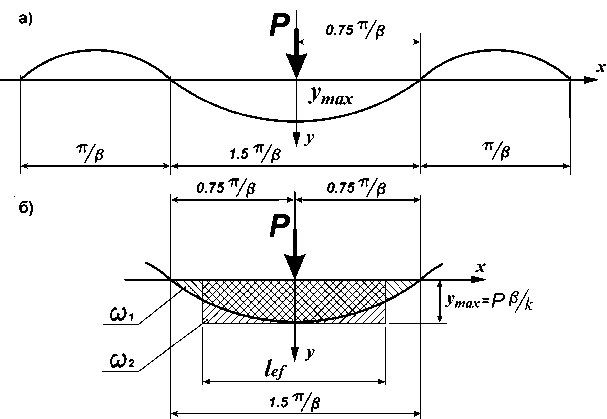
Рис. 4. Эпюры прогибов рельса как балки на сплошном упругом основании

пропорционально осадке поверхности основания, равного прогибу балки [7]:

q ( x ) = ky ⁽ x ) •                                   ⁽²⁰⁾

С учетом (19) выражение (20) примет вид:

q ( x ) = 0,5 P p^ e ^{- в x} ( cos в x + sin в x ) ] .       (21)

Из рис. 4, а видно, что график функции (21) представляет собой волнообразную кривую с постепенно уменьшающейся амплитудой , определяемой периодом функций cos в x и sin в x . Рассмотрим только ту часть кривой, которая ограничена нулевыми точками на расстоянии 1,5 п/в (рис. 4, б).

Из выражения (19) следует, что при x = 0 (начало координат) прогиб балки и перемещение основания достигает своей наибольшей величины V ( 0 ) = P в/ к .

Упругий прогиб рельса и перемещения основания будут равны нулю, когда cos вx и sin вx в уравнении (19) будут равны по величине, но противоположны по знаку. Это достигается тогда, когда вx = 0,75п и далее с добавлением числа п . Таким образом, упругий прогиб балки равен нулю п п при расстоянии x1 = 0,75 — ; x2 = 1,75 — и т. д.

Для простоты расчетов перейдем от криволинейной эпюры давления на упругую полуплоскость к равномерно распределенной на длине lef нагрузке q = 0,5Рв (рис. 4, б). Условную длину распределения найдем из равенства площадей криволинейной М| и прямолинейной М2 эпюр давления (рис. 4, б).

Площадь криволинейной эпюры равна:

0,75 п

Ю1= ®1 = 2 k J 0 75п в e в x (cos вx + sin вx) dx.

После интегрирования получим: м 1 = 1,0675 Рк .

Площадь прямолинейной эпюры ω₂равна: м = Р в l ef /2 к .

Из равенства ω 1 = ω 2 имеем:

l ef = 34/ Elpjk .                            (22)

Формула (22) позволяет оценить эффективность различных подрельсовых оснований для снижения уровня локальных напряжений в стенке подкрановых балок, которые вычисляются по формуле:

^ loc , y = Pj ^l ef ' ^ .

В качестве примера рассмотрим крановый путь, состоящий из сварной балки с толщиной стенки δ = 8 мм и рельса КР 70 (Ip=1082 см4; b = 12 cм), уложенный на низкомодульную резинометаллическую прокладку толщиной 8 мм. Модуль упругости прокладки Е = 0,5 кН/см2 при твердости резины по Шору HA = 75 ед. Коэффициент постели основания k0=0,5/0,8 = 0,625 кН/см3. Коэффициент податливости и условная длина распределения соответственно будут равны:

k = 0,625·12=7,5 кН/см²;

l_ef = 3 4 2,05 - 10⁴ - 1082/7,5 = 124см.

Условная длина распределения l_ef в стенке сварной балки, эксплуатируемой без низкомодульных прокладок, равна[5]:

l ef = 3,263/1082/0,8 = 36,0 см.

Выполненные расчеты показывают, что использование низкомодульной прокладки позволяет увеличить длину распределения локального давления в 3,4 раза, т. е. её эффективность, как конструктивного элемента для снижения локальных напряжений, составляет 340 %.

Использование формулы (22) для клепаных балокc коэффициентом податливости k =0,3·10⁴ кН/см²дает значение l ef = 34/2,05 - 1082/0,3 = 28 см, что меньше l_e f для сварной балки без прокладки. Это свидетельствует о том, что в клепаных балках длина распределения в значительной степени определяется мощностью склепанного пакета верхнего пояса, а не только моментом инерции кранового рельса, и подтверждает ранее высказанное предположение, что в клепаных балках крановый рельс не определяет НДС стенки.

Локальное напряженное состояние стенки балки может быть вычислено по формулам (2) с использованием методики, опубликованной в [7], или по методике упругой полуплоскости, изложенной в [9].