Использование модели связанных классических осцилляторов для описания резонанса Фано в плазмонной наносистеме

Возбуждение энергетического уровня лазерным импульсом является хорошо известной задачей квантовой электроники, и её решение для длинных импульсов с большим числом осцилляций детально описано [1, 2]. При использовании малоцикловых импульсов возникают специфические изменения двухуровневой системы, выражающиеся в нарушении монотонности зависимости вероятности перехода от времени в слабых полях и возможности управления заселением уровней с помощью чирпированных импульсов [3–5]. В целом ряде реальных физических систем возбуждённый уровень не является изолированным, и взаимодействие дискретного состояния с другими степенями свободы может быть описано в форме взаимодействия с зоной уровней. Так выглядят автоионизационные состояния [6, 7], возбуждённые состояния атомного ядра на фоне непрерывного спектра [8, 9], молекулярные электронные возбуждения на фоне колебательного спектра [10–12] или состояния примеси твёрдого тела, взаимодействующие со спектром матрицы [13]. Соответствующие резонансы, возникающие при возбуждении таких состояний, имеют характерную асимметричную форму, вызванную интерференцией состояний уровня и зоны. Теория резонансов дискретного состояния на фоне континуума была развита независимо Фано и Фешбахом, а сами резонансы, проявляющиеся в самых разных физических системах, в общем случае называются резонансами Фано – Фешбаха [14].

Развитие физики и технологии изготовления нано-размерных структур выявило наличие в них новых разнообразных резонансов Фано – Фешбаха [15], которые мы далее согласно принятой практике будем называть просто резонансами Фано. С точки зрения перспективы создания нанооптических и наноэлек-тронных приборов особый интерес представляют резонансы, обусловленные взаимодействием состояний в квантовых точках с акустическими [16] и оптическими фононами [17–19], а также плазмонами в металлических наночастицах и нанопроводниках [20–29].

Воздействие резонансного лазерного поля существенно влияет на структуру резонансов Фано – Фешбаха [30–33], изменяя как параметры, так и саму форму зависимостей. Если внешнее воздействие достаточно мало, то отклик системы становится линейным по полю так, что изменение средних значений операторов координат описывается классическими уравнениями движения связанных осцилляторов [34]. В работе [35] показано, что модель связанных осцилляторов подходит для описания различных резонансных явлений в фотонных системах: резонанс Фано, электромагнитно-индуцированная прозрачность, эффекты Керкера и Бормана.

Мы рассматриваем возбуждение двух связанных осцилляторов под действием переменной силы для демонстрации динамического формирования профиля Фано.

1.    Классическая модель

Интерференция Фано – универсальное явление, поскольку проявление деструктивной интерференции мод не зависит от характера среды. Важность резонансов Фано для физики наноструктур заключается в той информации, которую они содержат о конфигу- рации взаимодействующих мод и внутренних потенциальных полях в низкоразмерных структурах. Она может быть извлечена из картины интерференции волн в разных каналах. Классическая модель резонансов Фано состоит из слабо связанных между собой осцилляторов, возбуждаемых внешней силой [36, 37]. Резонанс Фано можно довольно просто моделировать, используя эквивалентные электрические колебательные системы [38].

Следуя [36], рассмотрим классические уравнения движения двух связанных осцилляторов

Q ( s ) = ( s ² + m 2 + Y i s )( s ² + м 2 + Y 2 s ) - v ²

найдём при условии малости параметра связи осцилляторов: m 2 - го ? >>  v . Невозмущённые корни при ( v = 0)

'n =^-y ± i ^^m2 j

^^^^^s

Y j ,

4,

n = 3, 4, 5, 6 .

Поправки за счёт взаимодействия осцилляторов 5 s ₃ , ₄ находятся из уравнений

^{5 s} 3,4

v ²

Х 1 + y 1 X 1 + m 2 x 1 + vx 2 = f ( t ), x ₂ + у ₂ x₂ + m 2 x ₂ + vx 1 = 0,

( ^{2 s} 3,4 ^+у 1 ) ( ^s 3,4 ^+m 2 ^+у 2 ^s 3,4 )

где v описывает упругую связь осцилляторов. Отклик

системы с нулевыми начальными условиями на произвольное воздействие будем искать с помощью преобразования Лапласа. В области изображений система уравнений (1) запишется как

s ² X 1 + у 1 sX 1 + m 2 X 1 + vX ₂ = F ( s ), s ² X ₂ + у ₂ sX ₂ + m 2 X ₂ + vX 1 = 0.

^{5 s} 5,6 =

( ^{2 s} 5,6 ⁺Y 2 ) ( ^s 52,6 ^{+m 2 +}Y 1 ^s 5,6 )

Тогда решения для трансформант имеют вид

X i ( s ) =

( s ² + m 2 + у ₂ s ) F ( s )

( s ² + m 2 + y 1 s )( s ² + m 2 +У 2 s ) - v ² ’

X i ( s ) = -

vF ( s )

( s ² + m 2 + y 1 s )( s ² + m 2 + У ₂ s ) - v ²

Отклик на гармоническое воздействие получается из (2) при подстановке s = i m , F ( s ) = 1. Отклик на произвольный импульс может быть найден обратным преобразованием Лапласа, в котором вклад отдельных осциллирующих компонент определяется вычетами в полюсах. Окончательные решения во временной области имеют вид

-' j l > ) - E jn ) e“ -                             (4)

_n Q ( s_n )

Здесь sn – значения корней полинома Q (s) в знаменателях уравнений (3), Q' (s) – производная Q (s), Pj (s) – функции в числителях уравнений (3). На больших временах колебания затухают для любого импульсного воздействия конечной длительности. Если на больших временах сохраняется гармоническая составляющая внешней силы, то устанавливаются стационарные колебания постоянной амплитуды. Рассмотрим отклик системы на внешнее воздействие в виде затухающего колебания f (t) = f,e-X‘ sin(mot), t > 0,                             (5)

имеющее преобразование Лапласа

F ( s )           ' -----2.                                        (6)

( s + X ) + m o

Для нахождения обратного преобразования Лапласа определим полюсы в уравнении (3) с учётом выбранной формы импульса. Полюсы F ( s ): s 1, ₂ = - X ± i m ₀, а полюсы

Для проведения конкретных расчётов мы взяли параметры [36] модельной системы: m 1 = 1 эВ, m 2 = 1,2 эВ, y i = 0,0025 эВ, у 2 =0,005 эВ, v = 0,1 эВ². Если для установившегося колебания под действием гармонической силы уровень возбуждения можно отслеживать по амплитуде колебаний, то для нестационарных режимов удобнее контролировать усредненный по осцилляциям квадрат амплитуды x ² _j ( t ) . На рис. 1 представлены результаты расчёта динамики возбуждения первого осциллятора модельной системы под действием монохроматического поля в области резонанса Фано. На врезке рис. 1 показаны частотные зависимости откликов модельной системы на монохроматическое поле единичной амплитуды с двумя характерными резонансными максимумами. Провал, характерный для резонанса Фано, вблизи второго максимума частоты означает, что отклик си-

стемы равен нулю.

|Х/(со)|, отн.ед.

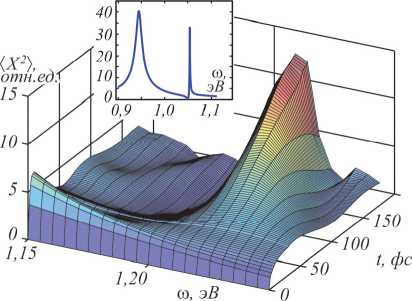
Рис. 1. Дисперсионно-временная зависимость резонанса Фано для системы двух связанных осцилляторов модельной системы при возбуждении гармонической силой f(t)=f o sin( ro t). На врезке показана дисперсионная зависимость возбуждения первого осциллятора модельной системы

Для спектрально узких резонансов и широкополосного импульса детали строения импульса становятся несущественными, и удобной формой представления силы становится постоянный по величине спектр, эквивалентный действию 5 -импульса. На рис. 2 представлены результаты расчёта динамики возбуждения системы

широкополосным импульсом. Наглядно видно отсутствие зависимости динамики возбуждения от несущей частоты, означающее универсальность линейного отклика системы на предельно короткий импульс.

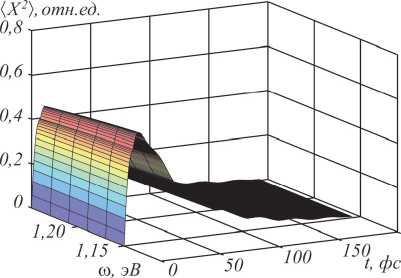
Рис. 2. Дисперсионно-временная зависимость резонанса Фано для системы двух связанных осцилляторов модельной системы при возбуждении импульсной силой вида f(t) =f o e ^{-t/ T} sin ( a t), т = 2,2 фс

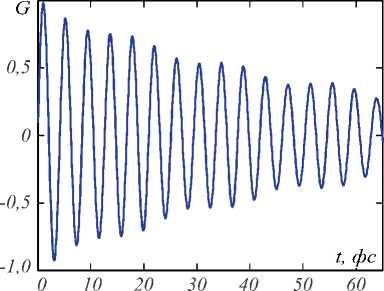
Рис. 3. Функция Грина G модельной системы. Расчёт на основе преобразования Лапласа

Фактически динамика системы при импульсном воздействии описывается... решением системы уравнений (1) при f ( t )= 5 ( t ), т.е. соответствующей функцией Грина G . В области изображений преобразования Лапласа такой импульс имеет вид F ( s )=1, а искомая функция Грина во временной области представляет собой сумму затухающих колебаний, удовлетворяющих начальным условиям x 1 (0) = 0, x (0) = 1 , x ₂(0) = 0, - x ₂(0) = 0 . Эти условия обусловлены тем, что действие 5 -силы на первый осциллятор изменяет его импульс на единичную величину, не меняя остальных начальных условий системы. Вычисленная функция отклика показана на рис. 3 и представляет собой сумму двух затухающих колебаний с периодом биения 82,6 фс.

Модель связанных классических осцилляторов позволяет описать плазмонные резонансы в наноструктурах [39-41]. Для системы, состоящей из оптически связанной квантовой точки (КТ) (нанокристалла) и металлической наночастицы, параметры плазмонного резонанса №1=2,118 эВ, у1 = 55,7 мэВ. Параметры КТ №2 = 2,11 эВ, у2 = 2 мэВ. Константа связи v = 60 мэВ2. Поскольку модель линейная, величина возбуждения влияет только на амплитуду отклика и не сказывается на его частотной или временной зави- симости, поэтому амплитуда возбуждения выбрана произвольно. На рис. 4 показана временная зависимость возбуждения системы, которая стремится к экспериментальным результатам [42] для больших времен.

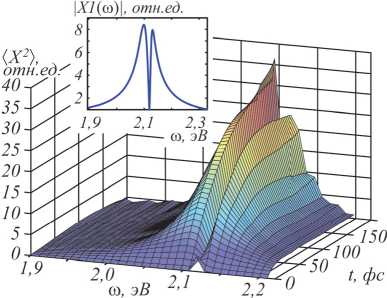
Рис. 4. Частотно-временная зависимость резонанса Фано для оптически связанной КТ (нанокристалла) и металлической наночастицы, возбуждаемой полем f(t)=f o sin ( a t). Дисперсионная зависимость системы представлена в виде врезки

Рис. 4 демонстрирует нарастание резонанса Фано под действием монохроматического поля. После определённого переходного процесса устанавливается стационарный рисунок с характерным узким провалом в спектральном центре.

2.    Асимметричные резонансы в связанных плазмонных системах

Интересный пример дает нам настраиваемая резонансная наноструктура Фано, состоящая из четырёх взаимодействующих наностержней [43]. Резонанс Фано в этой структуре обусловлен интерференцией дипольных мод. Эта система может быть описана расширенной моделью связанных осцилляторов. В такой модели система двух осцилляторов характеризуется резонансными частотами №1, ю2 и затуханием Y1, у2 в соответствии с безызлучательными потерями. Радиационное затухание двух дипольных осцилляторов выражается через полный дипольный момент системы Ptot=P 1 + P2 = а1 x 1 + а2x2, где Pi, P2 - дипольные моменты первого и второго осциллятора, x 1, x2 - их амплитуды и а1, а2 - поляризуемости. Предполагается, что пространственная протяжённость системы меньше четверти длины волны падающего света, а силы, приложенные к обоим осцилляторам, находятся в фазе. Чистая сила пропорциональна их поляризуемости f1,2 = а1,2 Eext.

Уравнение движения можно записать следующим образом:

2                     /1 /^Ч\ П . .    Г-*    / ,\ x + Y1 x1 + Ю1 x1 + vx 2 = (1/2) Ptot + a1 Eext (t), x 2 + Y 2 x 2 + ®2 x 2 + vx = (1/2) Pot + a2 Eext (t),

e • • где (1/2)Ptot - излучательная связь осцилляторов. Для падающего гармонического поля Eext (t)= E0 e 1юt колебания x 1, x2 гармоничны, так что x 1,2= X1,2 e1 “t, где амплитуды колебаний:

X 1 ( ω ) =^{α 1} a ^{22 -α 2} a ¹² E 0 , a ₁₁ a ₂₂ - a ₁₂ a ₂₁

X 2 ( ω ) =^{α 2} a ^{11 -α 1} a ²¹ E 0 .

a 11 a 22 ^- a 12 a 21

В рассматриваемой системе коэффициенты определяются как

α kk =ω k 2 -ω 2 + i γ k ω+ ( i /2) α k ω 3 , α 12 = ν + ( i /2) α 1 ω 3 ,

α 21 = ν + ( i /2) α 2 ω 3 .

Значение коэффициентов ω 1 = 1,55 эВ, ω 2 = 1,78 эВ, γ 1 =0,083 эВ, γ 2 =0,051 эВ, v =0,084 эВ², α 1 =0,128 эВ^–1, α ₂ = 0,131 эВ^–1 взяты из [43]. Для произвольной временной зависимости эффективность рассеяния света системы представлена квадратом модуля электрического дальнего поля, усреднённого по колебаниям | Esc I ^ I Х1 + Х 2 1. Для падающего гармонического поля он пропорционален квадрату модуля амплитуд ω 4 | X 1 + X 2 | 2 и может быть использован для моделирования спектра рассеяния [44]. Для близких резонансных частот можно принять, что они имеют среднее значение внутри частотного интервала. Следовательно, для ранее рассматриваемой системы, состоящей из КТ и металлической наночастицы ( ω 2 / ω 1 ) 4 = 1,015, можно положить это значение постоянным. Однако для данного случая плазмонной наноантенны это неверно, поскольку резонансы имеют разные частоты. Этот вывод подтверждается рис. 5, где разница между амплитудным откликом и рассеянием поля очевидна. Тем самым параметризация, представленная в [43],

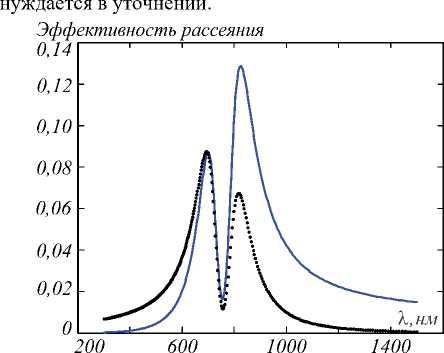
Рис. 5. Дипольная частотная характеристика системы |X 1 +X 2 | ² (сплошная линия) и зависимость эффективности рассеяния от частоты (пунктирная линия)

Параметризация системы, представленная в [43], после более точной спецификации определяется как ω 1 =1,146 эВ, ω 2 =1,64 эВ, γ 1 =0,01 эВ, γ 2 =0,195 эВ, v = 0,14 эВ 2 , α 1 = 0,195 эВ –1 , α 2 = 0,045 эВ –1 . Дальнейшие расчеты будут проводиться с уточненными параметрами системы, а также с учетом отклика ∞ ω 4 | X 1 + X 2 | 2 . Как показано на рис. 6, экспериментальная и модельная зависимости частоты довольно близки вблизи максимумов и минимумов.

Эффективность рассеяния 0,10 0,09 0,08 0,07 0,06 0,05 0,04 0,03 0,02 0,01

О

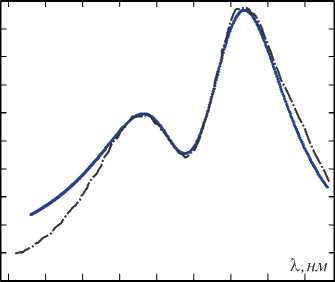
550     650     750     850     950

Рис. 6. Дипольная частотная характеристика системы ω4 |X 1 +X 2 | 2 (сплошная линия) и экспериментальная зависимость эффективности рассеяния от частоты [43] (штрих-пунктирная линия)

На рис. 7 показана временная функция отклика системы как решение G ( t ) = x 1 ( t ) + x 2 ( t ) после завершения действия ультракороткого импульса, имеющего δ -фор-му импульса и отклик в виде функций G ( t ) и a ( t ) ускорения a ( t ) = G ( t ). Коэффициент корреляции R =Corr( G , a ) =–0,937 указывает на некоторое отклонение от идентичности функций (исключая знак минус), что было бы справедливо для отклика системы

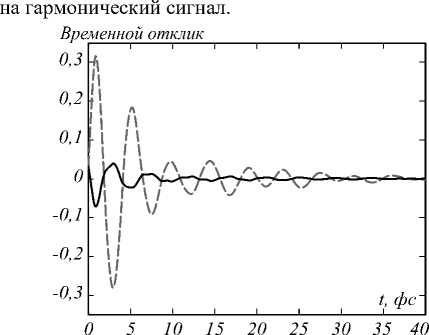
Рис. 7. Дипольный отклик G(t) (пунктирная линия) и ускорение a(t) (сплошная линия), пропорциональные рассеянному световому полю

Рассеянное поле Esc ( t ) для падающего света с произвольной временной зависимостью Eext ( t ) определяется свёрткой:

t

E sc ( t ) = ∫ a ( t - t 1 ) E ext ( t 1 )d t 1 .                          (10)

-∞

Принимая во внимание выявленные характерные ультракоротких импульсов (УКИ) в оптическом диапазоне, удобной формой их представления являются сигналы Габора с Гауссовой огибающей Eext (t) = e –(t/τ)2sin (ωt). На рис. 8 показана усредненная по осцилляциям интенсивность рассеяния, как функция от времени и несущей частоты падающего импульса с длительностью τ = 10 фс. Чётко проявляется двухгорбая структура рассеяния света в динамиче- ском процессе рассеяния импульсов, представленная в спектральном распределении.

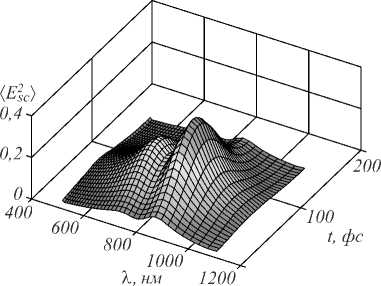
Рис. 8. Интенсивность рассеяния как функция времени и длины волны падающего импульса

Если измерять полный спектр рассеянного света, его можно вычислить как произведение эффективности рассеяния в частотной области на интенсивность спектра падающего импульса. Полученные спектры представлены на рис. 9. Сплошная линия для относительно длинного импульса с длительностью 10 фс воспроизводит спектр падающего света с амплитудой, соответствующей функции рассеяния. Более короткий импульс с длительностью около 2,2 фс демонстрирует двугорбые внутренние структуры, связанные с двухчастотным резонансным откликом наноантенны.

Спектр рассеяния 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1 О

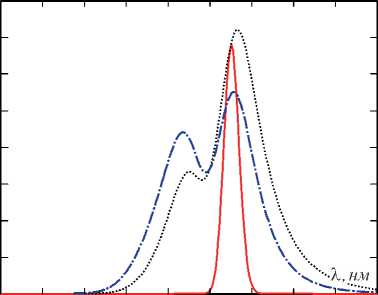
300    500      700      900     1100

Рис. 9. Спектр рассеянных импульсов Габора: длительность импульса 10 фс и несущая частота импульса ω = 1,55 эВ (сплошная линия); для импульса длительностью 2,2 фс (пунктирная линия) показан результат для ω = 1,55 эВ, а штриховая пунктирная линия соответствует несущей частоте 1,78 эВ

Заключение

Насколько известно, до сих пор не было получено точного решения для описания динамики возбуждения резонанса Фано в рамках классической модели двух линейных связанных осцилляторов при затухающем гармоническом воздействии. Проведено уточнение уравнений рассеяния в случае большой ширины резонанса, когда для корректного описания отклика необходимо учитывать не только существенное изменение амплитуды вынужденных колебаний си- стемы, но и самой частоты рассеяния в области резонанса. Впервые приведены результаты расчёта динамики формирования профиля резонанса Фано под действием импульса Габора в зависимости от несущей частоты.

Полученные нами результаты по временной зависимости формирования профиля Фано в действительности имеют более широкую область применимости, поскольку линейный отклик системы полностью описывается её дисперсионными свойствами. Такой вывод следует из возможности представления линейного отклика на импульс произвольной формы в виде интеграла Фурье с подходящей частотной зависимостью передаточной функции. Поэтому конкретная реализация линейного оператора, обладающего необходимым спектром, не сказывается на описываемых свойствах. Это позволяет использовать модель классических связанных осцилляторов для описания динамики самых различных линейных систем с резонансными характеристиками. Временной отклик системы может сильно варьироваться в зависимости от формы действующего импульса.

Частотные характеристики функции отклика могут быть измерены как путём частотного сканирования спектрально узким, перестраиваемым по частоте лазерным излучением, так и с использованием техники восстановления отклика по измерению корреляционной функции для УКИ [45]. Альтернативным способом получения полной характеристики линейной системы является измерение отклика на действие δ -импульса, позволяющее получить её функцию Грина. Близкие характеристики отклика дают УКИ со спектральной шириной, существенно превосходящей ширину резонансов системы. Для разных типов атомных, молекулярных и наносистем в качестве таких зондирующих импульсов могут использоваться фемто- и аттосекундные лазерные импульсы. Отметим, что экспериментальную проверку полученных результатов можно произвести, в частности, на классических механических колебательных системах, в RLC-цепях, а также измеряя рассеяние световых импульсов на металлических наночастицах различной формы [46].

Работа выполнена в рамках Государственного задания Министерства науки и образования РФ (задание № 3.9890.2017/8.9).