Использование модельных распределений в задаче анализа систем массового обслуживания с коррелированными заявками
Автор: Карташевский И.В.
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 3 т.20, 2022 года.
Бесплатный доступ
В статье рассматривается задача определения времени ожидания заявки в очереди в одноканальной системе массового обслуживания общего вида для случая, когда интервалы времени между поступающими заявками коррелированы. Для решения задачи предлагается осуществить декорреляцию указанных интервалов времени с использованием дискретно-косинусного преобразования. В общем случае для анализа произвольных распределений, входящих в выражение для декоррелированной последовательности, можно предложить подход, основанный на аппроксимации неизвестных плотностей модельным распределением. Вычисление кумулянтов и моментов случайных величин осуществляется весьма просто по сравнению с аналитическими методами. По найденному конечному набору кумулянтов всегда может быть воспроизведена с определенной погрешностью модельная плотность вероятностей. В общем случае для расчета среднего времени ожидания заявки в очереди необходимо определить корреляционные свойства и одномерную плотность вероятностей интервалов времени между поступающими заявками, синтезировать двумерную плотность вероятностей последовательности данных интервалов, обладающей измеренной корреляционной функцией, и далее рассчитать совместные моменты и кумулянты для коррелированных величин, по которым строится их модельная плотность.
Система массового обслуживания, корреляция, кумулянт, среднее время задержки
Короткий адрес: https://sciup.org/140300664
IDR: 140300664 | УДК: 519.872.7 | DOI: 10.18469/ikt.2022.20.3.02
Текст научной статьи Использование модельных распределений в задаче анализа систем массового обслуживания с коррелированными заявками
Одним из определяющих свойств современного телекоммуникационного трафика является корреляционная функция последовательности интервалов времени между элементами трафика. Поэтому методы классической теории массового обслуживания, основанные на решении интегрального уравне- ния Линдли, не применимы для описания и анализа систем, обслуживающих коррелированный поток заявок. Следовательно, для корректного использования аппарата теории массового обслуживания необходимо обеспечить представление коррелированного трафика последовательностью некоррелированных случайных величин.
Постановка задачи
Рассмотрим задачу определения времени ожидания заявки в очереди для системы G/G/1 в случае, когда интервалы времени между поступающими заявками коррелированы.
Если интервалы времени между заявками и интервалы времени обслуживания заявок независимы (как того требует классическая теория массового обслуживания [1; 2]), то для преобразования Лапласа распределения времени ожидания в очереди F ( x ) можно записать:
to j e — sxdF (x) = exp
—
A 1 to
£-j(1 — e"sx)dK(N)(x) , (1) n=1 N о где K(N) - N-кратная свертка распределения
K (x):
to
K (x) = j B (x + u) dA (u), (2)
A ( • ) - распределение интервалов времени между заявками на входе системы, B ( • ) - распределение интервалов времени обслуживания заявок.
N -кратная свертка K ( N ) ( x ) - это функция распределения суммы N независимых одинаково распределенных случайных величин с функцией распределения K ( x ).
Для решения задачи при коррелированных элементах в последовательности интервалов времени между заявками можно воспользоваться выражением (1), осуществив декорреляцию данных интервалов, которая может быть реализована при разбиении последовательности на блоки с дальнейшим использованием по отношению к каждому блоку декоррелирующих преобразований на основе, например, разложения Карунена – Лоэва [3], дискретно-косинусного преобразования [4] или вейвлет-преобразования (наиболее простой вариант можно получить с использованием вейвлет Хаара [5]).
Любой алгоритм декорреляции, примененный к блоку к оррелированных случайных величин У i , i = 1, N , даст в итоге блок некоррелированных величин v к того же размера, к = 1, N .
Декорреляция на основе дискретнокосинусного преобразования
При использовании для декорреляции дискретно-косинусного преобразования процесс декорреляции реализуется следующим образом. Если вектор Г = [у0, Y1, • • •, уN—1 ]т, составляющие которого суть коррелированные между собой интервалы времени между заявками с коэффициентами корреляции R01, R02, • R0 N—1, то для де- корреляции необходимо использовать некоторую матрицу W размером (N х N), удовлетворяющую соотношению WWT = I (I - единичная матрица), чтобы получить вектор Т с некоррелированными элементами такого же размера в виде т = wr.
В дискретно-косинусном преобразовании элементы матрицы W записываются в виде:
к п(2 m + w = a,, cos k, m k 2 N где
-
a 0 = yJN ’ a к = 1 N ’ k = 1, 2, • N 1.
Для N = 8 элементы матрицы Т вычисляются как
V к = £ у m w , m m = 0
где a0 = 2V2 ,
-
a, = 1, к = 1,2, • 7.
k 2
В выражении (3) у m , m = 0, 7 представляют собой значения случайных интервалов времени, во-первых, с известным одномерным распределением и, во-вторых, с известными корреляционными связями (коэффициентами) R 01, R 02, • R 0 N — 1 , которые могут быть получены на этапе мониторинга последовательности. Будем предполагать, что коэффициенты корреляции имеют значения:
R 01 = 0,63, R 02 = 0,376,
R 03 = 0,292, R 04 = 0,244,
R05 = 0,34, R06 = 0,19, R07 = 0,16, • что соответствует фрактальной последовательности с коэффициентом Херста H = 0,7.
При этом из (3) следует, что некор релиро ванные между собой значения V к , к = 0, N — 1 имеют разные одномерные распределения, определить которые чрезвычайно сложно. Так, например, согласно (3) элемент V i запишется как
V1 = к1 (У0 — У 7) + к2 (У1 — У 6) + + к3 (У2 —У5 ) + к4 (У3 —У4 )»
где к 1 = 0,49, к 2 = 0,416, к 3 = 0,2775, к 4 = 0,0975.
Количество слагаемых в выражении (5) равно N / 2, что объясняется косинусоидальным характером изменения значений ортогонализирующих коэффициентов wk m. Конкретные значения коэффициентов ki, i = 1, N/2 определяются как ki — |wim |, и проблема нахождения распределения ^1 связана с тем, что уm, m = 0, 7 коррели-рованы между собой.
Найти плотность вероятностей разности Y i - Y j можно через двумерное распределение f . i Y j ( x, У ) в виде: to
f(У) = J f(x, У + x)dx, (6)
Fy. (x) — 1 - e-(Xx>e,
_ k mk = E(xk) — л "Г
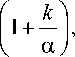
а саму плотность f ( x , y ) можно синтезировать на основе теоремы Склара [6] с использованием функции копулы [7]. При этом плотность f ,.Y. ( x , У ) может быть записана в виде:
f(x,У) = c(F (x), Fyj(У))f.,(x)f(x),
при учете корреляционных коэффициентов R Y Y элементов у i , i — 0, 7 ( mk - момент k -го порядка; Е - символ усреднения; Г ( - ) - символ гамма-функции).
Для простоты (без потери общности) положим Л = 1, а = 2. Тогда двумерная плотность f ,.Y. ( x , У ) на основе копулы (7) с учетом того, что все y i , i = 0, 7 имеют одно и то же распределение (8), примет вид:
f', Yj (x1, x 2 ) =
= 4
где
c ( F y . ( x ), F Y j ( У ) ) =
a2 c (u, v) du dv
- плотность копулы и u = F (x), v = F (у).
При использовании копул для синтеза двумерных плотностей корреляционные связи анализируемых последовательностей обычно учитываются через введение коэффициента ранговой корреляции Кендалла. Однако для копул C ( u , v ) семейства ФГМ (Фарли – Гумбеля – Моргенштерна) с полиномиальным расширением [7] вида:
C (u, v) = uv [1 + A(1 - up )(1 - vp)], (7)
где р - целое число ( p = 2,3, ...), имеется возможность установить количественное соотношение параметра A и коэффициента корреляции R (по Пирсону). При этом для параметра A из (7) могут быть установлены ограничения в виде:
Список литературы Использование модельных распределений в задаче анализа систем массового обслуживания с коррелированными заявками
- Клейнрок Л. Теория массового обслуживания / под ред. В.И. Неймана. М.: Машиностроение, 1979. 432 с.
- Cohen J.W. The single server queue. Amsterdam: North Holland Publishing Company, 1969. 695 р.
- Пугачев В.С. Теория случайных функций и ее применение к задачам автоматического управления. М.: Физматлит, 1960. 883 с.
- Сэломон Д. Сжатие данных, изображений и звука. М.: Техносфера, 2004. 368 с.
- Дремин И.Н., Иванов О.В., Нечитайло В.А. Вейвлеты и их использование // Успехи физических наук. 2001. Т. 171, № 5. С. 465–501.
- Nelsen R.B. An Introduction to Copulas. Lecture Notes in Statistics; 2nd ed. New York: Springer, 2006. 269 p.
- Balakrishnan N., Lai C.-D. Continuous Bivariate Distributions. New York: Springer, 2009. 684 p.
- Карташевский И.В. Использование копул в статистическом анализе телекоммуникацонного трафика // Инфокоммуникационные технологии. 2016. Т. 14, № 4. С. 405–412.
- Малахов А.Н. Кумулянтный анализ случайных негауссовых процессов и их преобразований. М.: Советское радио, 1978. 376 с.
- Кендалл М., Стюарт А. Теория распределений / под ред. А.Н. Колмогорова. М.: Наука, 1966. 566 с.
- Cook M.B. Bi-variate k-statistics and cumulants of their joint sampling distribution // Biometrika. 1951. Vol. 38, no. 1/2. P. 179–195.
- Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Наука, 1971. 1108 с.
- Прилепко А.И., Калиниченко Д.Ф. Асимптотические методы и специальные функции. М.: МИФИ, 1980. 107 с.