ИСПОЛЬЗОВАНИЕ НЕЙРОННОЙ СЕТИ КОХОНЕНА ДЛЯ КЛАССИФИКАЦИИ ЗАБОЛЕВАНИЙ СЕРДЕЧНО-СОСУДИСТОЙ СИСТЕМЫ

В настоящее время заболевания сердечно-сосудистой системы (ССЗ), наряду с онкологическими заболеваниями, диабетом и заболеваниями легких, входят в четверку наиболее распространенных причин смерти, средняя смертность от данных заболеваний составляет 17,9 млн. человек в год [1]. Выявить и определить заболевание на ранних этапах позволяют различные методы: ЭКГ (электрокардиография), ЭХОКГ (эхокардиография), КТ (компьютерная томография, МРТ (магнитно-резонансная томография) и другие.

Развитие технологий и, в частности, искусственного интеллекта, позволяет производить диагностику с помощью нейронных сетей различных архитектур. В настоящее время нейронные сети позволяют распознавать различные заболевания сердечно-сосудистой системы – аритмии разных видов, фибрилляцию тканей сердца – предсердную и не пре-предсердную, ишемическую болезнь сердца, и так далее.

При диагностике сердечно-сосудистых заболеваний методами искусственного интеллекта используются различные типы нейронных сетей. Наиболее часто исследуется применение сверточных нейронных сетей, например, сети AlexNet и различных ее модификаций [2], одномерных сверточных нейронных сетей (Convolutional Neural Networks, CNN) [3], применяются также радиально-базисные нейронные сети [4].

Постановка задачи

В статье приводятся результаты исследова- ния возможности классифицирования записей сердечного ритма нейронной сетью Кохонена с целью выявления заболеваний сердечно-сосудистой системы. Обучение нейронной сети Кохоне-на проводилось с использованием алгоритмов самообучения и векторного квантования (Learning Vector Quantization, LVQ).

Для проведения исследования были поставлены и решены следующие задачи:

– определение процедуры, на результатах которой будет обучена нейронная сеть;

– определение архитектуры сети;

– исследование влияния особенностей архитектуры на точность классификации;

– определение параметров обучения, обеспечивающих наибольшую точность классификации.

В рамках данной статьи, точность и эффективность классификации определялись как процент определения нейронной сетью правильного диагноза на классификационной выборке, состоящей из 400 записей, при этом выборка содержала равное число записей, ассоциируемых с каждым из диагнозов, распознаванию которых обучалась сеть.

Обоснование архитектуры нейронной сети

В статье [5] приводится описание архитектуры нейронной сети Кохонена, производящей диагностику трех заболеваний сердечно-сосудистой системы: аритмии (ARR), фибрилляции предсердий (AFF), сердечной недостаточности (CHF), а также диагностику нормального синусового ритма (NSR).

Нейронная сеть представляет собой множество классов, организованных в одномерную структуру, каждый из которых соотнесен с вектором числовых данных, изменяющимся в процессе создания и обучения нейронной сети.

Максимальная точность диагностики составляет 96%, что позволяет считать описанную архитектуру эффективной. Также к достоинствам стоит отнести простоту данной архитектуры по сравнению с нейронными сетями типа CNN.

Описание формата входных данных

Среди классических методов диагностики заболеваний сердечно-сосудистой системы наиболее распространенным является электрокардиография, результаты которой могут быть использованы для обучения нейронных сетей распознаванию и диагностике.

На практике нейронная сеть может быть обучена на различных типах данных, полученных путем преобразования результатов процедур. Нередко при обучении нейронных сетей классификации ССЗ применяются скалограммы [6], также могут использоваться записи работы сердца в виде аудиофайлов [7].

Также в качестве данных для обучения и классифицирования можно использовать численные векторы, описывающие длительность тех или иных участков кардиограммы. Обозначения участков кардиограммы приведены на рисунке 1 [8].

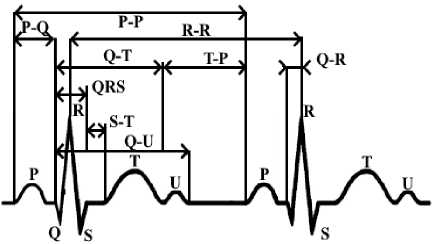
Рисунок 1. Обозначение участков ЭКГ

Представление в виде вектора чисел, характеризующего длительность участков электрокардиограммы, называемых «зубцами», «интервалами» и «сегментами» может быть применимо при обучении нейронной сети Кохонена, используемой, как правило, для классификации и кластеризации подобных данных. Также стоит отметить возможность представления результатов ЭКГ в форме временных рядов, которые могут быть использованы для обучения нейронной сети Кохонена и сетей других архитектур, например, многослойного персептрона.

Зубцы, характеризующие кардиограмму, делятся на типы P, T, S, R, Q, U. Физически зубцы описывают различные параметры электрической активности сердца, такие как степень сокращения и расслабления предсердий, а также раздачу импульсов по миокарду, и в норме образуют строго определенную последовательность, характеризующуюся конкретными временными параметрами [9]. Соответственно, справедливой будет постановка диагноза на основе совокупности данных временных параметров, образующих вектор.

Следует отметить роль упомянутых элементов кардиограммы:

– зубец P означает сокращение предсердий;

– зубец T означает расслабление желудочков;

– зубец Q характеризует начальное отклонение электрокардиограммы вниз, которое, в совокупности с зубцами R и S, описывает деполяризацию желудочков;

– зубец R характеризует первое отклонение ЭКГ вверх, позволяет судить о гипертрофии желудочков;

– зубец S так же, как и Q, характеризует отклонение вниз;

– зубец U не играет никакой диагностически значимой роли.

Периодичность возникновения данных зубцов, а также длительности сегментов (отрезков между соседними зубцами) и интервалов (отрезок от начала одного зубца до начала другого) позволяет диагностировать различные расстройства, поскольку имеются известные значения длительности данных отрезков ЭКГ, соответствующие норме, например, интервал PQ должен длиться 0,12 с, RR – от 0,6 с до 0,66 с.

Учитывая это, для обучения и тестирования нейронной сети Кохонена был выбран набор данных, состоящий из записей, описывающих временные параметры ЭКГ пациентов, страдающих аритмией, фибрилляцией предсердий, сердечной недостаточностью и тех, у кого наблюдался нормальный синусовый ритм.

Данные для обучения и тестирования были взяты с ресурса [10].

Общее описание проводимых экспериментов

Датасет был разделен на выборки в следующем соотношении:

– стартовая выборка: 100 записей;

– классификационная выборка: 400 записей;

– обучающая выборка (LVQ): 400 записей;

– обучающая выборка (для обучения алгоритмом самообучения): 400 записей.

Каждый их экспериментов, определяющих оптимальные параметры работы с сетью, состоял из следующих шагов:

– создание нейронной сети Кохонена, корректирующей во время процедуры создания параметры нейронов согласно алгоритму самообучения, или загрузка ранее созданной сети;

– выбор соответствующих алгоритму параметров обучения;

– обучение сети в соответствии с алгоритмом;

– проверка результатов обучения классификацией на соответствующей выборке.

В связи с архитектурными особенностями нейронной сети Кохонена, обучение ее любым алгоритмом, в конечном счете, сводится к изменениям значений элементов векторов нейронов, приводящим к сокращению Евклидового расстояния между вектором обучаемого нейрона и входным вектором.

Также стоит отметить, что порядок подачи на вход сети векторов является случайным на каждой итерации каждого эксперимента. Случайный порядок подачи необходим для предотвращения переобучения и адаптации нейронной сети к определению записей, ассоциированных только с одним диагнозом.

Таким образом, приведенные далее результаты описывают точность распознавания обученной в соответствии с определенным алгоритмом для определенных значений параметров нейронной сети при определении диагнозов записей классификационной выборки.

Определение оптимальных параметров самообучения

В [11] приводится описание алгоритма самообучения и алгоритма векторного квантования, наилучший результат был получен при гибридном обучении. Обучение заключается в изменении параметров нейронов путем инкремента значения разности расстояний между вектором выбранного нейрона и входным вектором, умноженного на коэффициент обучения, убывающий линейно. Таким образом, значение параметров изменения коэффициента, как и самого коэффициента, крайне значимы при обучении. На основе данных сведений были проведены исследования выявления зависимости точности распознавания от параметров самообучения нейронной сети и параметров дообучения предварительно обученной нейронной сети алгоритмом векторного квантования.

Результаты исследования зависимости точности классификации данных от параметров самообучения приведены в таблице 1.

Таблица 1. Процент средней точности распознавания сетью Кохонена в результате самообучения с различными параметрами

	Значение множителя коэффициента обучения
Значение декремента	1	0,75	0,5	0,25	0,15
0,001	90,26	89,94	90,32	90,47	90,54
0,002	90,22	89,96	90,26	90,36	90,41
0,005	90,68	90,2	90,21	90,57	90,42
0,01	90,67	90,18	90,16	90,4	90,32
0,015	90,26	90,05	90,37	90,52	90,34
0,02	90,29	90,4	90,18	90,31	90,46

Согласно полученным данным, наибольшая средняя точность классификации, равная 90,68%, была получена для сети, созданной со стартовым значением коэффициента обучения 0,13, декрементом коэффициента 0,003 и множителем коэффициента 1 при следующих параметрах самообучения: значение множителя равно 1, значение декремента – 0,005.

Стоит отметить, что максимальное значение точности составляет 93,25% и получено для сети с теми же параметрами создания при множителе коэффициента обучения, равном 1, и значении декремента, равном 0,01, при этом среднее значение точности распознавания для значений декремента 0,005 и 0,01 отличается на 0,01, соответственно, можно сделать вывод, что оптимальными параметрами самообучения являются следующие: значение множителя коэффициента обучения 1 и значение декремента от 0,005 до 0,01.

Также, анализируя результаты экспериментов, можно заметить, что разница между минимальной и максимальной средней точностью относительно невелика и составляет 0,72%, это означает, что на всем множестве выбранных параметров самообучение можно считать эффективным.

Исследование эффективности обучения алгоритмом векторного квантования

Алгоритм векторного квантования и область его применения описаны в [11], статья [5] описывает эффективность использования данного алгоритма для классификации результатов ЭКГ. Алгоритм векторного квантования (LVQ) относится к алгоритмам обучения с учителем. Однако может также применяться для улучшения точности классификации самообучающейся сети Кохонена. С учетом данных сведений были проведены эксперименты, определяющие среднюю точность обучения.

Результаты экспериментов по определению зависимости средней точности распознавания от параметров обучения алгоритмом векторного квантования приведены в таблицах 2, 3 и 4. Обучению подвергалась сеть, имеющая точность распознавания 89% и 36 классов. Была исследована эффективность обучения при 10, 20 и 30 эпохах обучения, константа обучения изменялась (убывала) линейно, согласно функции y = kx - b.

Количество эпох для экспериментов было выбрано с учетом возникновения проблемы переобучения, а также учетом числа классов, ассоциированных с каждым из диагнозов. Использовались малые значения декремента коэффициента обучения. Нелинейные функции изменения коэффициента не использовались.

Таблица 2. Процент средней точности распознавания сетью Кохонена в результате обучения алгоритмом векторного квантования при 10 эпохах обучения с различными параметрами

	Значение константы обучения
Значение декремента	0,1	0,15	0,2	0,25	0,3
0,001	93,85	94,29	94,27	93,73	93,24
0,002	93,47	94,08	94,18	94,04	93,87
0,003	92,79	94,14	94,28	94,3	94,1
0,004	92,79	93,8	94,2	94,19	94,23
0,005	92,93	93,53	94,2	94,44	94,45

Таблица 3. Процент средней точности распознавания сетью Кохонена в результате обучения алгоритмом векторного квантования при 20 эпохах обучения с различными параметрами

	Значение константы обучения
Значение декремента	0,1	0,15	0,2	0,25	0,3
0,001	93,86	94,12	93,82	93,57	93,29
0,002	93,42	94,22	94,47	93,89	93,67
0,003	92,85	94,09	94,4	94,17	93,52
0,004	93,05	93,93	94,26	94,325	94,16
0,005	93,3	93,77	94,43	94,415	94,48

Согласно полученным результатам, максимальное значение средней точности составляет 94,57% и получено для 30 эпох обучения, значения константы обучения 0,25 и значении декремента 0,005. Данное значение подтверждает эффективность применения алгоритма векторного квантования при решении задачи классификации заболеваний сердечно-сосудистой системы.

При этом, разность максимальных значений средней точности самообучения и алгоритма векторного квантования невелика, как и в случае с разностью максимальных значений, полученных путем самообучения и с применением алгоритма векторного квантования – 1,22% для средних значений и 3% для максимальных значений. Максимальное значение точности (94,75%) было получено для 30 эпох обучения, стартового значения константы обучения 0,25 и декремента 0,003. Таким образом, можно сделать вывод, что наиболее оптимальными параметрами алгоритма векторного квантования являются: 30 эпох обучения, значение константы обучения 0,25 и значения декремента коэффициента от 0,003 до 0,005.

Таблица 4. Процент средней точности распознавания сетью Кохонена в результате обучения алгоритмом векторного квантования при 30 эпохах обучения с различными параметрами

	Значение константы обучения
Значение декремента	0,1	0,15	0,2	0,25	0,3
0,001	93,65	94,315	93,88	93,375	92,87
0,002	93,58	93,92	94,22	94,06	93,68
0,003	92,9	94,08	94,33	94,55	93,95
0,004	93,5	94,05	94,45	94,44	94,24
0,005	93,65	93,98	94,53	94,57	94,49

Исследование эффективности гибридного обучения нейронной сети

Согласно экспериментам, максимальное значение точности классификации заболеваний сердечно-сосудистой системы по результатам ЭКГ было получено при гибридном обучении нейронной сети Кохонена и составило 96%. Результаты же эксперимента по выявлению средней точности гибридного обучения приведены в таблице 5.

Из приведенной таблицы видно, что наибольшее значение средней точности равно 93,14% и было получено при значении константы обучения 0,1 и декременте коэффициента 0,005. Максимальное значение точности классификации равно 96% и было получено при значении константы 0,15 и декременте 0,003.

Стоит отметить, что средняя точность гибридного обучения ниже, чем средняя точность обучения алгоритмом LVQ, то есть, в среднем, применение гибридного обучения менее эффективно, чем применение алгоритма векторного квантования в чистом виде. С другой стороны, максимальная полученная точность распознавания была достигнута именно при гибридном обучении, что может быть объяснено влиянием случайных параметров на обучение, в частности, порядка подачи векторов из обучающей выборки. Так как результат обучения зависит от последовательности поступления векторов из обучающей выборки, статистически более вероятно возникновение

«менее удачной» последовательности векторов, за счет чего снижается средняя эффективность обучения, однако предельное значение точности, которое может быть получено, остается достаточно высоким.

Таблица 5. Процент средней точности распознавания сетью Кохонена в результате обучения алгоритмом векторного квантования предварительно обученной сети при 50 эпохах обучения с различными параметрами

	Значение константы обучения
Значение декремента	0,1	0,15	0,2	0,25
0,001	92,75	92,4	92,1	91,46
0,002	92,65	92,51	92,26	92,13
0,003	92,19	92,53	92,33	92,33
0,004	93,04	92,57	92,38	92,36
0,005	93,14	92,59	92,37	92,26

Исследование влияния возможности постановки неопределенного диагноза на точность распознавания

Диагностирование заболеваний сердечно-сосудистой системы нейронной сетью Кохонена базируется на фиксировании количества записей, отнесенных к одному из классов сети и соотносящихся с тем или иным диагнозом, при создании и/или самообучении нейронной сети, что позволяет при классификации ассоциировать с входным набором данных некий диагноз на основе количественного соотношения записей диагнозов, отнесенных к классу, что дает возможность постановки комбинированного диагноза.

С точки зрения информативности, смешанный диагноз будет менее полезен, однако может быть использован для повышения точности распознавания диагнозов. Были проведены исследования по сравнению максимальной полученной точности распознавания на различных этапах работы с сетью для сетей, позволяющих и не позволяющих ассоциировать с классом более 1 диагноза.

Стоит также отметить, что уже на этапе создания выявлялись классы, ассоциированные с двумя диагнозами, при этом оба диагноза представляли какое-либо из заболеваний, то есть, можно сделать вывод, что даже в случае смешанной диагностики результат классификации будет точен как минимум в определении того, здоров ли пациент или болен.

Так как сведения об экспериментах, описанные в предыдущих таблицах, достаточны для общей оценки эффективности алгоритма, дальнейшая оценка эффективности оценивалась по максимальной полученной точности классификации.

Необходимо также упомянуть, что на этапе создания сети, помимо параметров коэффициента обучения (начального значения, делителя и декремента), присутствует параметр, характеризующий выделение новых классов в сети – пороговое значение ошибки. При определении наиболее подходящего нейрона сети, то есть обладающего наименьшим евклидовым расстоянием от вектора нейрона до входного вектора, значение расстояния сравнивается с пороговым. В случае превышения порогового значения в сеть добавляется новый класс, вектор параметров которого совпадает с входным вектором. Пороговое значение ошибки – это число, специфичное для нейронной сети, оптимальное значение которого зависит от среднего расстояния векторов данных.

Экспериментальные данные приведены в таблицах 6 и 7.

Таблица 6. Сравнение значений максимальных процентов распознавания заболеваний на этапе создания сети

Пороговое значение ошибки	Максимальный процент верных распознаваний для сети с одним допустимым диагнозом класса	Максимальный процент верных распознаваний для сети с несколькими допустимыми диагнозами класса
40	81,5	83
60	86,25	89
80	84,5	88,25
90	83,75	85,75
100	82,25	84,5

Изучив полученные результаты, можно сделать следующие выводы: возможность ассоциировать с одним из классов более одного диагноза повышает максимальную точность классификации на этапе создания и самообучения сети.

В проведенных экспериментах максимальное число диагнозов, ассоциированных с заболеванием, равнялось 2, значение пороговой ошибки при создании было равным 60, стартовое значение коэффициента обучения – 0,13. Исследование эффективности самообучения проводилось на сети, созданной с теми же параметрами и значением множителя коэффициента 1.

Повышение точности классификации может быть связано как с вероятностными причинами, основанными на снижении числа неверных диагнозов, которые могут быть определены при со- отнесении входного вектора с классом, так и на схожести случаев заболеваний, с которыми были соотнесены классы с комбинированным диагнозом, в частности, AFF (Atrial Filling Fraction – доля наполнения предсердий) и CHF (Congestive Heart Failure, застойная сердечная недостаточность).

Таблица 7. Сравнение значений максимальных процентов распознавания заболеваний при самообучении сети

Значение декремента коэффициента обучения	Максимальный процент верных распознаваний заболевания для сети с одним допустимым диагнозом класса	Максимальный процент верных распознаваний заболевания для сети с несколькими допустимыми диагнозами класса
0,001	91,5	92,25
0,002	87,5	93
0,005	88,25	92,75
0,01	91,75	93,25
0,015	91,25	93
0,02	88,25	93

Заключение

В работе представлены результаты исследования применения нейронной сети Кохонена для классификации заболеваний сердечно-сосудистой системы. Результаты показывают эффективность применения нейронной сети Кохонена одномерной архитектуры, позволяющей ассоциировать с классом более одного диагноза.