Использование нелинейных вероятностных критериев для решения задач адаптивной фильтрации

Разработанные на сегодняшний день методы решения задачи идентификации-оценивания параметрически неопределенного динамического объекта, функционирующего в условиях возмущающих воздействий, предполагают, как известно, расширение его вектора состояния за счет вектора неизвестных параметров с последующим оцениванием всего расширенного вектора [1–4]. При подобном подходе N неизвестных параметров увеличивают размерность интегрируемой системы уравнений оценок с учетом симметрии матрицы

N ² ( 3

ковариаций на величину -—- + 1 — + M I N , где M — размерность вектора состояния системы, что существенно влияет на число параметров, допускающих практическую возможность идентификации.

Более того, при этом, как правило, принимается весьма упрощающее допущение о постоянстве идентифицируемых параметров на интервале наблюдения, что для подавляющего большинства реальных ситуаций оказывается условием невыполнимым, а в общем случае существенно снижает потенциальную точность оценивания.

Таким образом, поиск новых путей решения задачи параметрической идентификации, свободных от вышеупомянутых ограничений, представляет собой очевидный научный и практический интерес. Ниже предлагается подход, позволяющий не только избежать перечисленных недостатков традиционного метода, но и повысить потенциальную точность идентификации за счет использования вместо среднеквадратичного критерия более общих вероятностных критериев, зависящих от плотности распределения и обеспечивающих достижение потенциально большей точности. Для дальнейшего решения поставленной задачи сформулируем ее следующим образом.

ПОСТАНОВКА ЗАДАЧИ

Пусть нелинейный стохастический динамический объект, наблюдаемый зашумленным нелинейным измерителем

Z = Н ( X , t ) + W ,               (1)

где X — наблюдаемый вектор состояния, H ( X , t ) — известная нелинейная вектор-функция наблюдения, W — центрированный белый гауссовский шум с матрицей интенсивности D _W , описывается векторным дифференциальным уравнением

X = Uo (X, t) + U (X, t) + V, где Uo (X, t) — известная нелинейная вектор-функция, U (X, t) — вектор-функция с параметрической неопределенностью, V— центрированный белый гауссовский шум с матрицей интенсивности DV .

В общем случае вектор U ( X , t ) можно представить в виде

U (X, t ) = S (X )a (t), где S (X) — известная нелинейная функция-матрица, a (t) — искомый вектор неизвестных параметров, и записать уравнение объекта как

X = U _o ( X , t ) + S ( X ) a + V .        (2)

Для решения задачи адаптивной фильтрации (идентификации-оценивания)   в соответствии ра (Ф =-р

с вышеизложенным необходимо, чтобы искомый вектор a ( t ) доставлял оптимум некоторому заданному обобщенному вероятностному функционалу J , зависящему от апостериорной плотности вероятности (АПВ) р ( X , t ) процесса X , причем в общем случае нелинейно.

Анализ физического существа решаемой задачи показывает, что в качестве наиболее адекватной формы минимизируемого функционала J целесообразно использовать аддитивную совокупность двух функционалов, оптимизация первого из которых J1 =| Ф1 [р(X, t)] dX должна обеспечить X минимум неопределенности (максимальную информативность) идентифицируемого вектора a , а второго J2 = jФ2 [a (X, t)] dX — минимум его T

"энергетики" (в соответствии с принципом Ферма) на заданном (конечном или текущем) интервале времени T , т. е.

J = J Ф 1 [ р ( X ,t ) ] d X + j Ф 2 [ a ( X , t ) ] d X .

XT

При этом в соответствии с постановкой задачи функцию Ф1 можно выбирать как ядро функционала энтропии Шеннона (Ф1 = -р ln р) или Фише- d ln р d ln р dX ][ dX

T

) (т. н. "информаци-

онных функционалов"), а Ф ₂ — в виде классической квадратичной "энергетической" формы, заданной на текущем интервале времени

J 2 = j a ^T a d t = j Ф 2 ( a )d t.

t ₀ t ₀

Очевидно, что приведенные формы функционалов J1, J2 не являются единственными. Так, если apriori известна форма g (X, t) функции АПВ, то Ф1 можно выбирать, например, в виде положи тельно определенных функций (р - g), р ln— р

(ядро функционала Кульбака), | р - g | и др. Если известны пределы существования процесса (2) X * = [ X min , X max ] , то функционал J 1 можно выбрать из условия минимума вероятности существования процесса (2) вне интервала X * :

Xmin

J 1 = 1 - j р d X = j р d X + j р d X ,

X.             —caX

*

и т. д., исходя из особенностей решаемой задачи.

Таким образом, окончательно исследуемую задачу можно сформулировать как задачу поиска вектора a , доставляющего минимум функционалу

t

J = j Ф 1 ( X , р )d X + j Ф 2 ( a )d t ,       (3)

X *                         1 0

определенному на множестве функций АПВ р , удовлетворяющих решению известного уравнения Стратоновича для объекта (2) и наблюдателя (1):

/ = -div[(U (X,t) + 5(X)a)р] + d t L                         J

+"2" div [div ( Dv • р)] + [ F ( X, t)-F (t)] р =

= - div( 5 a р) + Q (р, X, t), где div — символ операции дивергенции; div — символ операции дивергенции, применяемой к каждой строчке матрицы;

F ( X , t ) = - 2 [ Z - H ( X , t ) ] T D W [ Z - H ( X , t ) ] ;

F ( t ) = j F ( X , t ) р ( X , t ) d X .

-TO

Так как

- div( 5 a р ) =

= -[div(5(1)р) - div(5(2)р) - div(5(k)р)]a =

= 50 (X, р )a, где S0 — вектор-строка, Si — i -й столбец матрицы S , то приведенное уравнение АПВ будем использовать далее в виде:

^д р = 5 o ( X , р ) + Q ( р , X , t ) .       (4)

РЕШЕНИЕ ЗАДАЧИ

Для решения поставленной задачи используем тот известный факт, что при неотрицательно определенной критериальной функции (как в рассмотренных выше вариантах) для обеспечения ее минимального значения в каждый момент времени достаточно, чтобы производная ее по времени, взятая с обратным знаком, имела максимум [3]. Отсюда для исследуемого случая получаем условие для определения идентифицируемого вектора параметров a :

max ( a )

{- J }=

= max - ( a )

-J

*

^Э Ф X P ) dP ^ X^tld x + ф ( a ) 1

др d t           ² ’

Подставляя в (5) выражение для правой части уравнения (4) имеем следующее уравнение относительно a :

с традиционной). Отсутствие же допущений о неизменности неизвестных параметров на интервале оценивания позволяет осуществить процедуру адаптивной фильтрации с принципиально большей точностью.

Для иллюстрации возможности эффективного практического использования предложенного подхода рассмотрим следующий пример.

( Q o + 5 o a ) d x + Ф 2 ( а )\ = 0- d a d dp '

X

*

Из последнего вытекает окончательное уравнение для определения искомого вектора a :

-PA 5 d x Jffi,       (6)

X* dP          da решение которого осуществляется, исходя из конкретного вида функции Ф2 . Так например, для предложенной выше квадратичной формы функции Ф2 (a) уравнение (6) принимает вид

-fM J dp

X *

5 ₀d X = 2 a ^T ,

откуда a = — . % (5o ^     (7)

Очевидно, что в результате проделанных построений функцию АПВ, обеспечивающую искомое оптимальное решение поставленной задачи адаптивной фильтрации, необходимо формировать из решения уравнения, полученного в результате подстановки выражения (7) в уравнение (4):

^p = Q ( p , X , t ) - 1 5 ₀J ^d Ф ^' ^P ) 5 T ( X ) d X . (8)

d t                2 X *     d p

Важно при этом отметить, что уравнение (8) полностью по структуре совпадает с уравнением Стратоновича (4), являясь интегро-дифференциальным уравнением в частных производных. Более того, совпадение их размерностей приводит, по существу, к практически одинаковым вычислительным затратам при формировании тех или иных алгоритмов фильтрации на базе известных методов[1–4] (что при отсутствии расширения размерности оцениваемой системы за счет вектора неизвестных параметров a сокращает, как было отмечено выше, размерность интегрируемой сис- n2 (3

темы оценок на -2- + 1 2 + M \ N по сравнению

ПРИМЕР

Стохастический нелинейный объект, описываемый уравнением

X = a1 X + a 2 X2 + a 3 X3 + V, X (0 ) = 0.1, где a1 = 3cos0.51, a2 = 2sint, a3 = 4e-tsin0.251 — параметры, неизвестные apriori наблюдателю; V — белый центрированный гауссовский шум с интенсивностью DV , наблюдается с помощью измерителя

Z = 1.5 X2 + W, где W — белый центрированный гауссовский шум с интенсивностью DW .

Оценивание процесса X с одновременной идентификацией вектора a = [ a 1 , a ₂, a ₃ ] ^T требуется осуществить, исходя из условия минимума функционала, традиционно используемого в задачах идентификации динамических объектов с полностью параметрически неопределенной структурой:

J = J ( Z - 1.5 X ² ) 2 D W p ( X , t ) d X + J a ^T a d t .

-^                                       0

Следуя приведенным рассуждениям, выражение для идентифицируемого вектора a было получено в виде

dp 1",( Z -1-5 X 2 )2 a = 2D -^        W p + X— dX i dP 2 X p + X2 — dX 3 X2 p + X3 -dp L          dX J dX, или, учитывая известное соотношение

-^                    -^

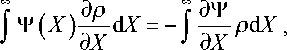
где T — произвольная нелинейная функция, то

a =

W -то

X ²

X ³

X ⁴

p ( X , t ) d X .

АПВ, в свою очередь, формировалась на основе решения уравнения

^ = - div — Г X X2 д t        Dw L то

-то

Г X : 1 . .

z - 1.5 X ² ) X ³ p ( X , t ) d X +

X ⁴

1 D dp - -1

2 V д X ² 2 D W

( Z - 1.5 X ² ) 2

-

то

J ( Z - 1.5 X ² )² p ( X , t ) d X p,

-то

численное решение которого осуществлялось методом прямоугольных сеток с шагом A X = 0.5 в области X , = [ - 30,30 ] на временном интервале [ 0,40 ] с с шагом формирования измерений A t = 0.1 с. Оценка процесса X при этом была сформирована по критерию максимума АПВ, определяемого на каждом временнóм шаге методом случайного поиска. Общая ошибка оценивания, усредняемая на интервале [30, 40]с, не превысила 18% от текущего значения процесса, при этом максимальные отклонения компонентов идентифицируемого вектора a от истинных значений составили: для a ₁ — 7%, a 2 — 11 %, a 3 — 5 %. Затраченный при этом объем вычислений позволяет сделать вывод о возможности осуществления процедуры идентификации в масштабе времени поступления реальной измерительной информации, т.е. в реальном времени.

Таким образом, полученные результаты свидетельствуют об эффективности практического использования предложенного параметрического подхода как с точки зрения точности идентификации и оценивания, так и объема вычислительных затрат.