Использование объектно-ориентированного моделирования при решении вопросов оптимального управления предприятием

Исследования, проводимые в области экономики, все чаще требуют использования экономико-математических моделей и возможности их дальнейшей адаптации к решению практических задач экономического толка.

Нам необходимо построить экономикоматематическую модель задачи оптимизации с учетом выполнения определенных требований продиктованных промышленным процессом:

• 1.    Математическая модель промышленного процесса должна существовать, помимо, должны существовать переменные процесса, For citation

  Lapshina M.L., Lukina O.O., Lapshin D.D. Use of object-oriented simulation in solving issues of optimal enterprise management. Vestnik VGUIT [Proceedings of VSUET]. 2022. vol. 84. no. 1. pp. 288–294.

• 2.    Требуется наличие и экономической модели промышленного процесса, учитывающей прибыль от реализации продукции, предоставления сопровождающих услуг и т. д.

• 3.    Методы оптимизации содержат независимые процесса, необходимые для отыскания значения функции цели, определенной экономикоматематической моделью.

This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International License

которые должны быть адекватными в вычислительном плане и с которыми легко работать и которые легко управляемые. Нужно заметить, что используемые материалы, оборудование, человеческий ресурс – все это объединяется и учитывается моделью.

Как правило, математическую формулировку оптимизационной задачи, записываем с использованием следующих составляющих S ( a ), a e A_adm, где A_adm соответствует множеству подходящих параметров или функции a , т. е. подходящую область. Заметим, что цена, как и структура ограничений, соответствующих A adm , существенно отличаются. Также, используемая структура является ключевой составляющей при решении вопроса о применении модели в определенной сфере [1, 2].

Проектировщик должен уточнить категорию, к которой относится сформулированная задача, а также определить какой метод или алгоритм решения наиболее оптимален при решении.

Материалы и методы

Воспользуемся одним из подходов к моделированию систем, который наиболее полно отразит максимально удобный отбор переменных, параметрических значений, а также непосредственно организации самой математической модели, направленной на упрощение модели в целом. Отметим, что на практике, вообще говоря, пользуются возможностью свободы моделирования. Если воспользоваться полученной свободой в разумных пределах, то существенно облегчится решение уравнения оптимизации:

• 5 « , t ) = min{ S ( a ) | x' = f ( x , a , t), x ( t ) = ^ } (1) u e U

Заметим, что модель такого вида подразумевает в некотором виде оптимизационный метод или схему контроллера обратной связи по состоянию, с учетом того, что линейная модель даст некое динамическое уравнение с наложением простых ограничений. Безусловно, здесь необходимо учитывать накопленные знания самого разработчика, которые, могут существенно упростить процесс. Но, не надо стремиться к решению различных проблем единственным способом, т. к. мы априори

Зачастую, приложив некоторое усилие, можно построить закон оптимального управления, его использование носит только приблизительный характер.

Становится понятным, что цель решения многих задач заключается в построении такой системы, которая работает без сбоев, а также эта система должна обладать более высокой производительностью, по сравнению с используемой ранее [3–5]. Такой подход приводит к рассмотрению идеальной задачи по управлению сложной системой. В связи с этим, при описании управленческой задачи, как оптимизационной задачи, целевую функцию надо записать в виде стоимостной функции, для которой необходимо отыскать экстремум (он может быть максимумом или минимумом). Зачастую, такой формализованный подход приходит к следующему соотношению tftf

S ( a ) = J g o ( y ( 5 ), a ( 5 ), 5 ) ds = J f , ( x ( 5 ), a ( 5 ) 5 ) ds t 0                                                  t 0

или S ( a ) = ^ ( а ( t^ )) = Ф ( x ( t_f ))                (2)

Будем понимать, что а ( 5 ) соответствует управляемому выходу. Воспользовавшись соотношением вида y = q ( x , a , t ), t e I = [ t ₀, tj ] приходим к формуле, которую определяет состояние системы [4]. Целесообразно отметить, что оба подхода для функции стоимости полностью равнозначны. Действительно, это так, так как суммирование состояния x и х ' = ( x^T , x_n+ J^T , с учетом подстановки Ф = x _n+1 будем иметь полную равнозначность. Заметим, что, сочетание подобных видов функции стоимости t_f

Ф (x (tf)) + S (a) = J f (x (5), a (5), 5) d5     можно t0

использовать в случаях, когда точность реализации условий в точке k (x(tj ), tj ) = 0 или х(ty) = ху не существенна. Существуют моменты, когда решение задач с отсутствием определенных граничных точек может быть существенно проще с учетом хорошего математического аппарата. Объединяя наши исследования, мы пришли к построению модели оптимального управления с непрерывным временным интервалом и со стандартным набором параметров, где оценка tf

J ( и ) = Ф ( x ( t f _f )) + j f , ( х ( s ), и ( s ), s ) ds = min t 0

относится к uCUadm, где Uadm определено: динамической системой: х' = f(х,и,t) t); граничными условиями: х(t0) = х0; k (x(tf), tf) = 0; условиями ограничения контроля: h(и) < 0 и h(и,х,t) < 0 ограничения состояния: g(х,t) < 0 или G(х, t) = 0 при разрешении проблемы вида х' = f (х, и, t), t е I = [t0, ty ], х (t0) = х 0, k (х (tf), tf) = 0, х (tf) = Xf, х (t0) = х (ty) = a, h (и) < 0 и h (и, х, t) < 0, g (х, t) < 0, G (х, t) = 0

с оценкой tf

J (и) = Ф (x (tf)) + j f,(х (s), и (s), s) ds t 0

Для дальнейшего решения можем воспользоваться тремя способами: принципом максимума Л.С. Понтрягина, принципами динамического программирования Р. Беллмана, принципами параметризации управления. Все эти подходы существенным образом облегчают исходную задачу отыскания оптимизируемых функций до более простой, т. е. до задачи с краевыми значениями области большой размерности, в основе которой положен принцип максимума или задачи параметрической оптимизации, здесь, в основе лежат принципы динамического программирования и параметризации [6-9].

Здесь, требуется отметить, что правильное применение первых двух подходов даст возможность нахождения абсолютного минимума, а также, значимым является то, процедура оптимизации что, параметризация должна быть неукоснительно реализована для нахождения подходящего приближения истинного математического решения, а также для нахождения возможного математического оптимального значения для конкретного типа задач [10]. Это можно получить, воспользовавшись параметрическими значениями, которые были найдены с использованием принципа максимизации результатов оптимального управления.

Принцип максимизации параметров является обобщением требуемых условий оптимальности вариационного исчисления, используемого для отыскания решения задач в непрерывном временном интервале. Подобный подход помогает отыскать требуемые условия, весьма существенные для большого сегмента задач, помогающих сформулировать характеристики и отыскать претендентов в оптимальные характеристики управления параметрами всей системы.

Принципы динамического программирования были определены для многоэтапного подхода решения оптимизационных задач. Что и определяет его использование при решении задач с дискретным временным интервалом, но иногда такой подход можно рассматривать как один из способов решения задач по отысканию оптимума параметров. При исследовании всех предпосылок к решению, итогом использования такого принципа является отыскание абсолютного экстремума [11-13].

При решении типичных управленческих проблем на перспективу, как правило, пользуются формулировками, требованиями и оценками, обусловленными неопределенностью требований и лингвистических понятий, что существенным образом усложняет процедуру построения оптимальных моделей, в основе которых лежат количественные данные, которые могут быть заданы только количественными и оценочными значениями вводимых параметров.

Все это может привести к тому, что математическая модель, соответствующая начальной постановке задачи примет достаточно грубую форму. Возникает предпосылка для построения вероятностной модели, которые тоже содержат ряд узких мест из-за того, что отсутствуют требуемые объемы статистических данных, невозможностью смоделировать прогностическое поведение системы на основе предшествующей информации, а также возникающих дополнительных сложностей при реализации проблем стохастического характера.

На настоящем этапе, в условиях нестабильности экономического рынка все чаще экономико-математические модели строятся с использованием элементов нечеткой логики. Практическая реализация подобных математических подходов подтвердила, что подобная реализация задач многокритериальной оптимизации наиболее полно отражает существо реальной проблемы и помогает, в результате, построить наиболее квалифицированное решение.

Такие подходы к отысканию решения задач в вопросах многокритериальной оптимизации служат логическим продолжением использования детерминированных подходов в условиях, когда требуется произвести выбор наиболее подходящего решения с использованием только одной из нескольких возможных альтернатив, при этом, коэффициенты предпочтения отдельных функций цели или непосредственно значения этих функций для каждой альтернативы будем задавать с использованием логических терминов. Смысл значений функций цели в каждом альтернативном случае обозначим, используя логическую систему вида «очень низкое», «среднее», «очень высокое». Необходимо заметить, что часть пространственных ограничений при принятии управленческих решений может описываться лицом, принимающим решения, на понятийном уровне.

Тогда проблема многокритериальной оптимизации может быть истолкована с использованием понятий нечеткой логики.

Тогда, каждую планируемую альтернативу A ЛПР, обозначает воспользовавшись некоторым нечетким множеством M , которое соответствует степени интерпретирует степень результативности каждой из функций цели в конкретной альтернативе. Воспользуемся функцией принадлежности, представим множество M_k следующим образом д [ f ( X | A ) ] : = = f ( x i A k ) ^ [ 0,1 ] . Используемые функции принадлежности можем записать в виде матрицы принятия решений (таблица 1):

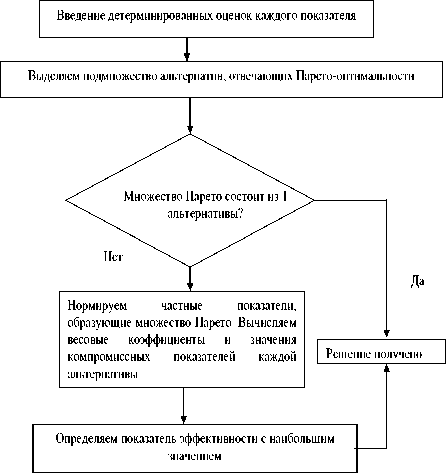
Рисунок 1. Структурная схема алгоритма принятия многокритериального решения

Figure 1. Block diagram of the multicriteria decisionmaking algorithm

В процессе анализа значений показателя эффективности двух диаметрально противоположных значений альтернатив мы можем воспользоваться разными детерминированными величинами:

– математическим ожиданием

T

Ф » ( A k ) = m_t { f_t ( A )} = E b k в , b k = -( b T + b k ); = 1                  ²

– среднеквадратическим отклонением;

T                          ²

Ф » ( A k ) = - { f ( A )} = — Z [ m { f ( A )} - b k ] в T ¹ ; = 1

Таблица 1.

Первоначальные значения для принятия решений

Table 1.

Initial values for decision making

	f ( X )		f ( X )		f n ( X )
A 1	Д 1 [ f ( X I A	1 1 )].	A -[ f ( X I A	; )]•	Д п [ f„ ( X I A	1 ) ]
… A r	д [ f ( X I A	!r ) ]	A -[ f ( X I A	r ) ]	Д п [ fn ( X I A	1r ) ]
A k	д [ f ( X I A	!k 4	A -[ f ( X I A	k 4	Д п [ f n ( X I A	1k ) ]

Структура алгоритма выбора наилучшего решения среди множества альтернативных вариантов, каждый из которых определяется множеством показателей, представляется в следующем виде (рисунок 1).

– вероятностью того, что значение соответствующего показателя будет меньше или равно некоторым заданным значениям данного показателя:

b k

Ф-k (Ak ) = P{f (A ) > bk } = J f (x 1 Ar )dx

-to

+to

Ф-k (Ak ) = P{f (A ) < dk } = J f (x I Ar )dx bk

Запишем следующим образом величину показателя, получение которого обеспечивается с вероятностью, не ниже наперед заданной:

Ф » ( A k ) = { b k I p [ f ( A ) >  b k ] >  p _ft }

Ф -k ⁽ A k ) = ^{ d k | P ^[ f ⁽ A ) ^ d k ^] >  Y k ^}

Кроме того, в качестве показателей могут быть рассмотрены моменты более высоких порядков. Предполагаем, что условие <_Re или >_Re

Lapshina M.L. et al. Proceedings of VSUET, 2022, vol. 84, no. 1 гарантирует условия приоритетности одной функции распределения случайной величины перед другой в сторону, соответствующую знаку.

Функции распределения i -го показателя эффективности альтернативы A соответствует абсолютная приоритетность относительно функции распределения данного показателя A_l

P^{fl ( A r ) >  b ik ^} ^Re P ^{ f ⁽ A i ) >  b ik ^}, в   смысле

P{ fl(Ar ) > bik } >Re P{ f(Ai) > bik },  если выпол няется каждое из следующей системы неравенств:

ф«⁽ A r )> Фи⁽A i );Ф зqi ⁽A r )> Ф зqi)At );q =V-. Q; ^

Ф 5 qi) Ar ) ^— Ф 5 qi ⁽ A ); q =I-. Й;

Ф 2Х A r )^— Ф 21 ⁽A i ); Ф 4qi ⁽A r )> Ф 4 qi ⁽Ai); g =i,-, G; ^ Ф б qi) A r ) ^— Ф б qi ⁽ A i); g = ⁱ ,-, G 2 ;

ИЛИ     p{fl(Ar ) > bik } ^Re P{ f (Ai) > blk }, в смысле   p{ f (Ar ) > bik } —Re p{ f (Ai) > bik }, в случае выполнения каждого из неравенств системы (3) – (4), в случае не выполнения бы одно из условий (3) – (4), то можно говорить об условиях относительного предпочтения [9–10]. Необходимо заметить, что специфика, поставленных задач, приводит к тому, что некоторых из детерминированных знамений в комплексных оценочных показателях функции распределения может и не быть. Такое может произойти когда положить значения весовых коэффициентов α равными 0. При решении практических задач наиболее частыми являются следующие ситуации:

• 1)    a = 1, а все остальные показатели значений весовых коэффициентов равны 0, т. е. мы должны учесть математическое ожидание функции распределения;

• 2)    а ^ 0, а ^ 0, ^а все остальные значения коэффициентов равны 0, т. е. нам необходимо учитывать математическое ожидание и дисперсию функции распределения.

В качестве интегрированных показателей критериев оценки продуктивности альтернатив воспользуемся следующими компромиссными показателями:

F * ( A r ) = z w фX A r ); F " ( A r ) = z w ф - ( A r ), г = 1                                           i = 1

где0 ≤ w _i ≤ 1, i = 1,..., n ; ∑ ⁿ w _i = 1

i = 1

Наиболее эффективное компромиссное решение должно, с одной стороны, принадлежать множеству альтернатив, а с другой – множеству наиболее эффективных решений [14].

Если в модели принятия решений множество значений векторов локальных целевых функций Z = F(x ) = | Z^_n и множество допустимых значений G = G представлены нечеткими множествами, то логическое эффективное компромиссное решение D ищется как некоторое нечеткое множество, которое принадлежит пересечению этих первых двух нечетких мно-жеств D е { Z i Q Z 2 П..Л Z_n Q.- G П...П G m } .

Альтернатива   A∗ , удовлетворяющая условию    ^ [F(X | A*)] = max ^ [F(X | A )],

D                1—r—K D является оптимальным решением сформулированной задачи.

Заключение

Таким образом, введение и вычисление различных детерминированных оценок эффективности каждого частного показателя и первого шага алгоритма исключения с использованием подтвержденного факта абсолютного предпочтения подмножества альтернатив, не принадлежащих оптимальному множеству Парето, после введения обобщенных показателей эффективности как каждого из частных показателей, с учетом наложенных на них требований, так и обобщенных показателей эффективности каждой альтернативы, последующие шаги алгоритма решения задачи полностью совпадают с алгоритмом принятия решений.