Использование пакета Simulink для опорно-параметрического моделирования переходных процессов в автоматизированных системах участков магистрального газопровода

Введение. Для эффективного управления магистральными потоками природного газа, а также диагностики и прогнозирования состояния транспортной системы особое значение имеет возможность математического или имитационного моделирования объекта. Это, прежде всего, касается задачи моделирования динамических процессов транспортировки газа в реальном времени [1]. Процесс транспортировки на участке магистрального газопровода описывается характеристиками потока газа, который в связи с пространственной протяжённостью по свойствам можно отнести к сплошной среде. Подобные процессы описываются в теории гидромеханики, гидро- и газовой динамики, а уравнения, описывающие эти процессы, являются уравнениями в частных производных, определённых для двумерных функций пространства и времени.

Анализ публикаций показал, что рассмотренные в монографиях математические модели газовой среды либо являются слишком общими, либо приведены к какому-то конкретному виду воздействия, например перемещение поршня в сосуде с газом. Поэтому актуальной задачей является получение и исследование применимости математической модели процесса транспортировки технологического агрегата, при минимальном количестве допущений; построение алгоритма, допускающего моделирование реакции на произвольные граничные и параметрические воздействия.

Серьёзной проблемой компьютерного моделирования являются математические особенности модели, такие как нелинейность, пространственно-временная многомерность, большое количество дифференциально-интегральных связей, определяющих необходимость применения численных методов приближённого интегрирования.

Численное моделирование различных технологических процессов всё больше и больше применяется для выявления нештатных ситуаций в моделируемом объекте, уменьшения количества брака при протекании какого-нибудь технологического процесса. Наибольшую техническую завершённость получили те технологии моделирования, которые основаны на моделях математической физики и газогидродинамики, т. е. на тех моделях, которые в докомпьютерный период были реализованы как лабораторные установки. Большое количество теоретических исследований, в частности изучение свойств моделей при предельных переходах, были проведены и опубликованы для моделей сплошной среды — газа, жидкости, кристаллов, электромагнитного поля.

Ещё одной развитой областью приложения численного моделирования являются важные для народного хозяйства технологические процессы. К наиболее законченным решениям в этой области относятся компьютерные модели струн, мембран, балок, тепловых полей в твёрдых веществах, линий электрической и оптической связи, потоков, обтекающих летательные аппараты и плавсредства.

Моделирование накопительно-транспортировочных переходных процессов, протекающих в газотранспортной сети, недостаточно хорошо изучено. Большая часть публикаций посвящена моделированию статических режимов, оптимизации режимов компрессорных агрегатов и методам диагностики самого газопровода как аппарата транспортировки. В данной работе моделируются динамические процессы перераспределения плотности, скорости и давления газа в результате переноса и распространения колебаний в движущемся по газопроводу газе.

Теоретический анализ задачи. Исходная математическая модель, представляющая изотермический процесс (режим, характерный для трубопроводов дальней транспортировки газа при его грунтовой прокладке) передачи потоком газа массы вещества и преобразования его механической энергии, описывается математической системой следующего вида:

Эр _ 5£ .

dt 8х '

д£       £  д£    f £ )   R • Т   8г   4  .     £ at     р ах   (р) у    ах  D р

Здесь р = р (х, t), w(x, t) иг =

£ (х, 0 = р (х, f) ■ w(x, f) — плотность и скорость тра йе портируемого газа, а также переменная состояния (ПС) потока газа, имеющая физический смысл массового расхода, соответственно. Обе переменные изменяются в общем случае в пространстве и во времени. Константы модели и начальные условия для переменных состояния заданы следующими значениями: R = 8,3144 Дж/моль К; 7Ь = 303 К; ц = 0,01604 моль; Ро = р (0, 0) = = 47,7521 кг/м3; £0 = 506,268 м2; D = 1,22 м; А = 0,000661 м4/с3 [1].

Рассмотрим подход к дискретизации параметров р = р (х, t) и г = г^х, t) модели (1) — (2) на примере более простой модели переноса концентрации вещества [2]. Разобьём процесс протекания на элементарные объёмы — ячейки (см. рис. 1). Допустим, что в пределах ячейки концентрация постоянна, тогда концентрацию на каждом участке можно характеризовать одной переменной — Си сопоставить её с одной точкой внутреннего пространства участка. Множество таких точек называется пространственной сеткой.

Пространственно-временная аппроксимация градиентов в узлах этой сетки (а иногда и между ними), позволяет получить аппроксимированную математическую модель, описываемую системой дифференциальных уравнений, которые можно решить с помощью различных числен ных методов. Такой подход, в котором сетка строится по пространству, а во времени модель сохраняет свои континуальные свойства, называется полудискретизацией.

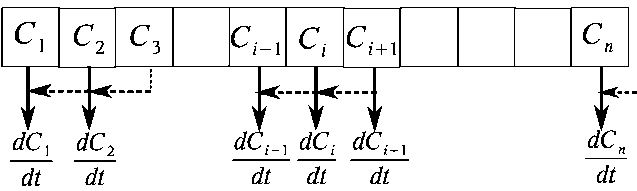
Рис. 1. Пространственная сетка и расчётная схема моделирования процесса передачи концентрации вещества

Возможности современных пакетов программ в плане программной реализации алгоритмов, построенных на описанных методах, позволяют не только использовать стандартные методы из библиотек подпрограмм инженерных расчётов, но и осуществить блочно-модульное построение модели подобного распределённого объекта. Наиболее эффективной и компактной может быть ячеечная модель любого распределённого процесса в среде пакета Simulink за счёт использования возможностей межблочной передачи векторных сигналов и применения синтаксиса языка системы MATLAB для дополнительной обработки подобных векторных сигналов.

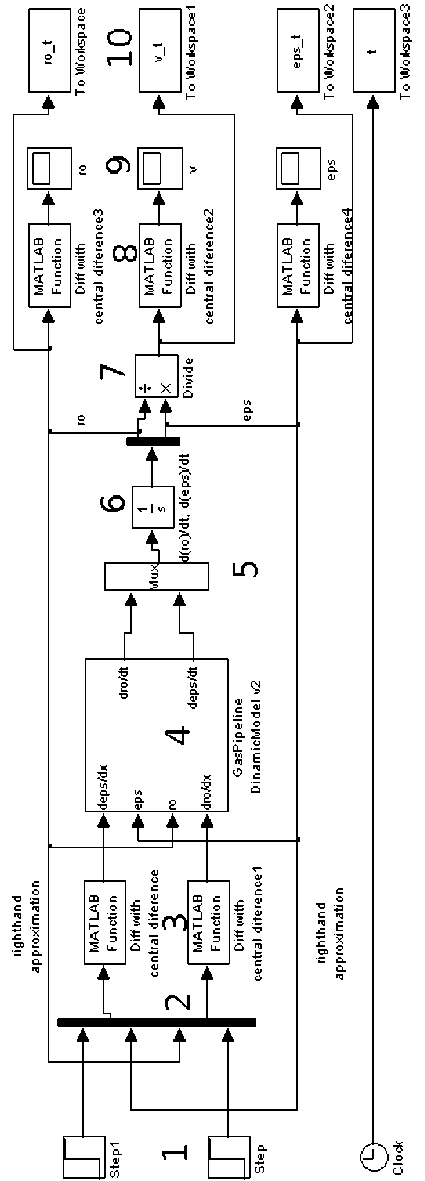
Рис. 2. Модель распределённого объекта в среде пакета Simulink

Например, при реализации ячеечной модели участка магистрального газопровода (1) — (2) элементы этого языка позволяют непосредственно в схеме вычислять конечные разности для аппроксимации градиентов (рис. 2) в (1) — (2). Эти же возможности позволяют обеспечить инициализацию векторного интегратора одномерным вектором начального состояния.

В состав схемы моделирования входят: 1 — программный формирователь ступенчатого параметрического перехода; 2 — мультиплексор, используемый для сведения значений граничных параметров с сигналами о состоянии для вычисления градиентов; 3 — дифференциатор первого порядка точности, основанный на следующей формуле вычисления приращения между дискретными аргументами:

№=()i-1-)rl.                            (3)

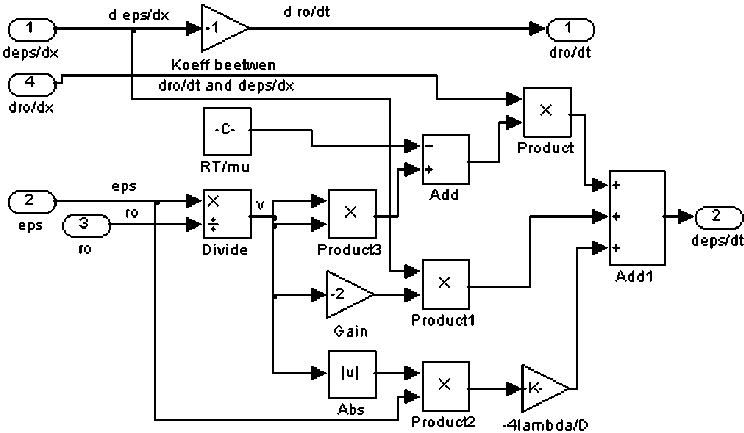
Блок 4 реализует моделирование конкретных законов накопления массы, импульса, энергии (рис. 3) при движении, соотнесённых с узлами сетки, обеспечивая сохранность этих параметров в движущемся потоке газа. Мультиплексор 5 из двух векторных сигналов об изменении состояния формирует один общий, который затем интегрируется блоком 6. Делитель 7 вычисляет сигнал, характеризующий скорость потока газа. Группа блоков 8 обеспечивает выборку каждого десятого сигнала для наблюдения на осциллографах 9 и создания истории изменения состояния в рабочей области системы MATLAB 10.

На рис. 3 показан модуль схемы, осуществляющий аппроксимацию градиентов, входящих в (1), (2), перерасчёт их по этой модели в величины, характеризующие интенсивности накопления, и, в соответствие с моделью (1) — (2), равных производным параметров р и £.

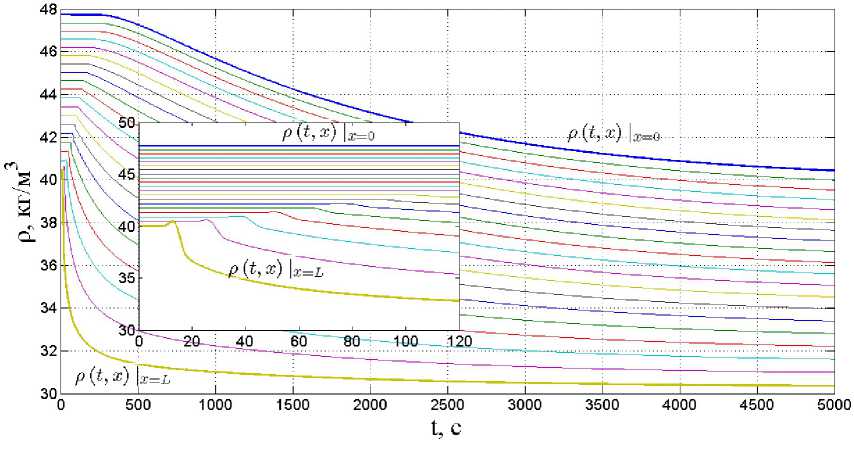
Рис. 5. Переходные процессы по плотности в сечениях участка магистрального газопровода

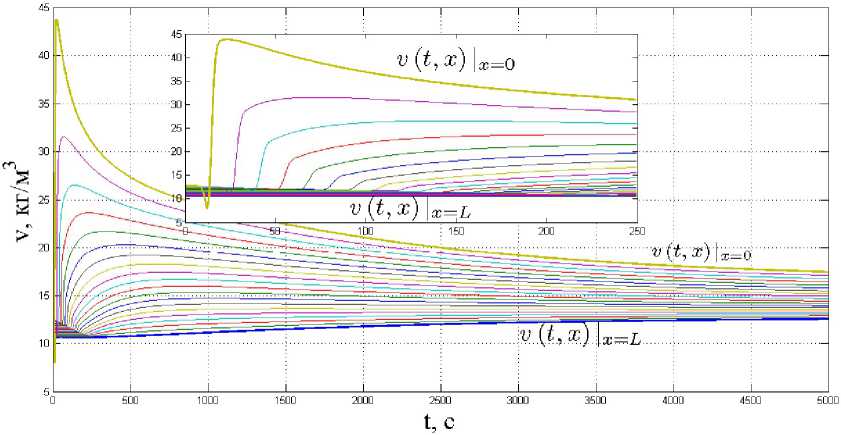
Рис. 6. Переходные процессы по скорости потока в сечениях участка магистрального газопровода

Наиболее исследованными параметрами распределённых объектов являются их статические профили, которые измеряются датчиками и моделируются в контурах АСУ ТП устройствами промышленной автоматики. Поскольку моделируемую систему можно рассматривать как сложный нелинейный объект, то его статический профиль отождествляется с его аттрактором (притягивающим многообразием). В силу процессов самовыравнивания плотности и диссипационных процессов, динамические процессы по переменным, характеризующим состояние объекта, должны затухать. Именно такое поведение компьютерной модели свидетельствует о том, что погрешности аппроксимации и вычислений не накапливаются, а нивелируются модельной вязкостью и дисси- пацией. Из сказанного можно сделать вывод, что установившееся значение параметров модели динамики должно соответствовать конкретизированным уровням статических профилей.

Результаты исследований. Эксперименты с однонаправленными и разнонаправленными разностями, аппроксимирующими градиенты расхода и плотности, показали, что можно добиться устойчивого математического моделирования ударных волн и явления массопереноса, если в уравнении баланса массы (1) использовать противопотоковые (левосторонние) пространственные аппроксимации, а для уравнения импульса разности по потоку — правосторонние.

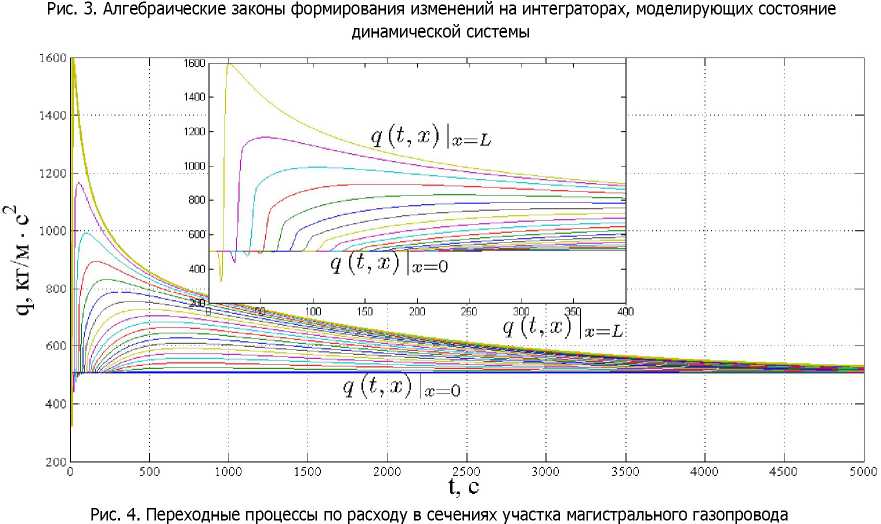
Имитационные исследования показали устойчивость переходных процессов, которые сходятся к уровням, соответствующим профилю, просчитанному после изменения расхода на входном участке и плотности на выходном. Графики (рис. 4—6) построены для случая 75 % уменьшения ПЛОТНОСТИ СКаЧКОМ В МОМеНТ Времени 1_В0здействия = 1 с.

В результате получена компьютерная модель переходных и установившихся режимов транспортировки природного газа. Эта модель позволяет провести исследование применимости многосеточных методов моделирования, основанных на том свойстве модели, что переходные процессы разделяются на две группы — быстрые и медленные (см. рис. 4—6). Данная модель зволяет создать и протестировать алгоритмы моделирования с повышенным по пространству рядком точности, за счёт применения методов сплайн-дифференцирования — это позволит пользовать более грубую пространственную сетку.

попо-ис-

за-