Использование программных комплексов при изучении студентами специальных дисциплин

Программа обучения студентов инженерных специальностей включает в себя обязательное изучение таких дисциплин, как «Информатика», «Программирование» и др. Как правило, эти предметы рассчитаны на 1-й и 2-й годы обучения. Без их регулярного использования в учебной деятельности многие полученные знания теряются безвозвратно. Это вызывает сожаление,

поскольку в работе, например инженера-машиностроителя, значительное количество времени занимают рутинные расчеты, которые с успехом можно автоматизировать с помощью известных программных комплексов.

В этой связи актуальной является задача применения полученных знаний студентами-старшекурсниками для решения конкретных проблем, связанных

непосредственно с их будущей специальностью. Например, одной из важнейших задач, требующей решения при проектировании металлорежущего станка, является определение центра масс. Точное определение положения центра масс позволяет рационально спроектировать фундамент станка и осуществить безопасную и удобную его транспортировку. Программный комплекс MathCAD позволяет с успехом решить эту проблему, а вместе с тем вспомнить навыки работы с комплексом, увидеть возможность его конкретного технического применения.

Методика расчета центра масс состоит в следующем:

– выбирается система координат (обычно рекомендуется за точку отсчета принять один из нижних углов основания станка);

– узлы станка аппроксимируются простыми пространственными телами (блоками) типа «цилиндр», «параллелепипед», «призма» и др.;

– указываются координаты аппроксимирующих тел относительно осей X, Y, Z (начальные и конечные точки) и координаты центров масс каждого блока;

– принимаются приблизительные коэффициенты заполнения блока α для каждого узла (0,1<α≤ 1) (принято считать блоки заполненными равномерно).

– рассчитываются объемы аппроксимирующих тел с учетом коэффициента заполнения;

– рассчитываются массы тел;

– рассчитываются координаты центра масс станка по формулам:

n

Em xx ii v _ i=1_________ x 0       n

Z mi

i = 1

n

Z mx yi y 0 = ^---

Z mi

= 1

n

Z mix zi z 0 =    n ,

Z m i i = 1

где m_i – масса i -го блока;

• x _i, y_i, z_i – координаты центра масс i -го блока.

Объемы аппроксимирующих тел с учетом коэффициента заполнения блока и их массы рассчитываются по классическим формулам. Точность расчета, разумеется, зависит от степени детализации станка, т. е. от количества аппроксимирующих элементов.

Расчеты по определению центра масс станка, несмотря на их относительную простоту, являются весьма громоздкими и требуют значительных затрат времени (известны системы автоматизированного проектирования, которые позволяют автоматически определить центр масс детали или узла, но нашей задачей является повторение полученных по информатике знаний и изучение возможности их использования для прикладных технических задач).

При расчете центра масс с применением MathCAD алгоритм расчета состоит в следующем:

• –    ввести значения координат отдельных узлов станка;

• –    вычислить координаты центра масс каждого узла;

• –    рассчитать объем каждого узла;

• –    рассчитать массу каждого узла;

• –    рассчитать центр масс станка.

Удобным является использование матриц (векторов), размерность которых соответствует количеству отдельных элементов (блоков), на которые разбивается металлорежущий станок (при этом студентам очень полезным будет вспомнить матричную алгебру).

Рассмотрим особенности каждого этапа расчета центра масс станка.

На первом этапе следует ввести значения координат отдельных узлов станка. Так как система станка рассматривается в трех измерениях, следует ввести 3 координаты: X, Y и Z.

Серия « Естественные и технические науки »

ВЕСТНИК Мордовского университета | Том 25 | № 1 | 2015

Каждый узел (или блок) имеет начальную и конечную координаты. Примем обозначение НX и КX для начальной и конечной координат узла по оси X соответственно, НY и КY – для начальной и конечной координат узла по оси Y, НZ и КZ – для начальной и конечной координат узла по оси Z. При этом обозначения могут быть произвольными.

Расположение конкретных значений координат в матрице соответствует номеру соответствующего блока.

На следующем этапе нужно определить координаты центра масс каждого узла.

Координата центра масс узла находится как половина суммы начальной и конечной координат:

HX + KX

X = 2 '

HY + KY

• ^— 2 ,

HZ + KZ Z .

В результате расчета создается матрица (вектор) для каждой переменной X, Y и Z, включающая столько элементов, сколько имеется узлов (или блоков).

На третьем этапе следует определить объем каждого блока, чтобы затем вычислить его массу.

Как известно, для тел в форме параллелепипеда, что характерно для большинства аппроксимирующих тел узлов металлорежущего станка, объем определяется как произведение длин всех сторон.

Длину каждой стороны можно вычислить как разность начальной и конечной координат:

A — KX - HX ,

B — KY - HY ,

C — KZ - HZ .

В итоге получаем новые матрицы A, B и C, которые характеризуют длины сторон каждого блока.

Коэффициенты заполнения для каждого блока также записываем в виде отдельного вектора. Обозначим его, например, как F.

Для попарного перемножения каждого элемента полученных матриц используем значок векторного произведения на соответствующей панели инструментов. Однако, если блок имеет форму цилиндра, а не параллелепипеда, то значение конкретного элемента матрицы следует ввести отдельно, а уже затем рассчитать объем каждого блока. Нумерация элементов матрицы начинается с нуля.

На четвертом этапе необходимо определить массу каждого узла. Для этого используется известная формула произведения плотности (удельной массы) узла на его объем.

Так как считаем, что узлы станка выполнены из стали, принимаем удельную массу, равную 7 800 кг/м3. Используем эту величину в качестве константы, на которую необходимо умножить вектор объема V0.

Однако, если в конструкции используются другие материалы, то не представляет особой сложности ввести соответствующую величину удельной массы. В этом случае следует предусмотреть для нее отдельную переменную.

Объем с учетом коэффициентов заполнения блоков обозначим, например, как VV, вектор масс блоков – М.

На последнем этапе расчета нужно определить центр масс станка по отдельным координатам X, Y и Z.

Обозначаем координаты центра масс станка как X0, Y0 и Z0. Для расчета используем известные формулы и соответствующие значки на панели инструментов MathCAD:

_ Y(M х X )

X 0 —--------,

S M

• Y 0 — ^YL, £ M

Z 0 _— S ( M X Z )

S M '

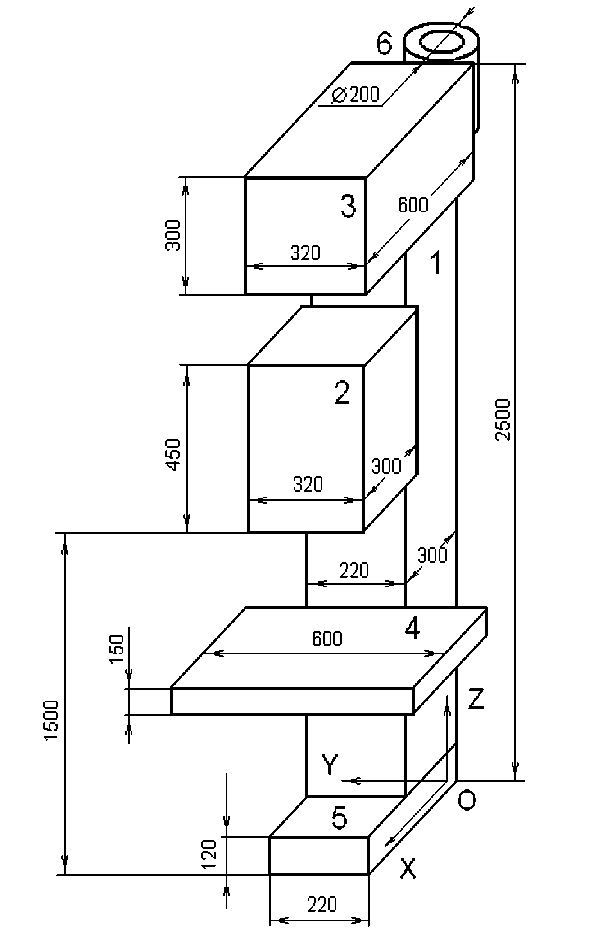
Рассмотрим расчет центра масс с применением MathCAD сверлильного станка с конкретными размерами (рис. 1).

Станок состоит из следующих узлов: 1 – колонна; 2 – шпиндельная бабка; 3 – коробка скоростей; 4 – стол; 5 – основание; 6 – электродвигатель.

Серия « Естественные и технические науки »

Р и с. 1. Сверлильный станок

Аппроксимирующими телами уз- ля. За аппроксимирующее тело элек-лов станка являются параллелепипе- тродвигателя принимаем цилиндр ды, за исключением электродвигате- (рис. 2).

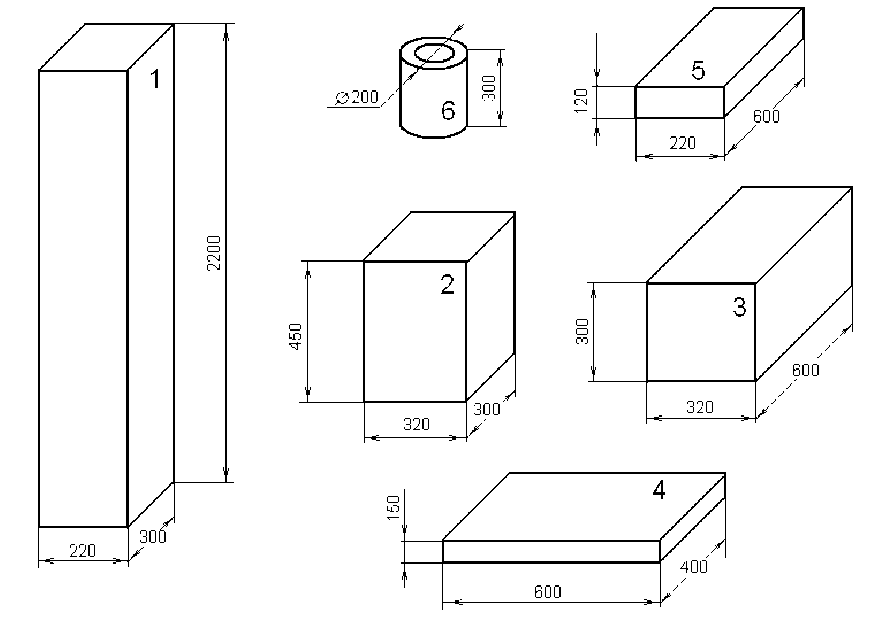
Р и с. 2. Узлы станка

Матрицы начальной и конечной координат будут состоять из 6 элементов. В MathCAD они имеют следующий вид:

– для координат X:

ВЕСТНИК Мордовского университета | Том 25 | № 1 | 2015

HX : =

( 0,0 л		' 0,0 '
0,3		0,62
0,0	KX : =	0,6
0,0		0,7
0,0		0,6
. 0,0 V		L- 0,2 V

;

– для координат			Z:
	" 0,0 ^		Г 2,08 )
	1,5		1,95
	2,2		2,5
HZ : =		KZ : =
	1,0		1,15
	0,0		0,12
	2 2 V ^’ 2		2 5 V 2,5 2

Затем рассчитываются координаты центра масс каждого отдельного узла.

Результаты расчета центра масс отдельных узлов сверлильного станка:

– для координат Y:

	' 0,0 ^		' 0,22 "
	- 0,05		0,27
HY : =	- 0,05 - 0,19	KY : =	0,27 0,41
	0,0		0,22
	. 0,01 ■		. 0,21 ,

	" 0,15 ^		" 0,11 ^		" 1,04 "
	0,46		0,11		1,725
=	0,3 0,35	• т : =	0,11 0,11	,Z : =	2,35 1,075
	0,3		0,11		0,06
	0 )		. 0,11 2		ч 2,35 >

Результаты расчета размеров сторон аппроксимирующих тел:

	< 0,3 ^		< 0,22 ^		< 2,08 )
	0,32		0,32		0,45
A : =	0,6 0,7	, B : =	0,32 0,6	' C '	0.3 0,15
	0,6		0,22		0,12
	02 V		V 0,2 V		V 0,3 V

Значения объемов тел параллелепипедов получены попарным умножением элементов матриц, характеризующих размеры сторон, а для элементов, характеризующих размеры цилиндра, вводим следующие значения:

• –    для 6-го элемента матрицы А – значение — х h (h - высота аппроксимирующего цилиндра);

• –    для 6-го элемента матрицы В – значение диаметра цилиндра (электродвигателя);

• –    для 6-го элемента матрицы С – значение диаметра цилиндра (электродвигателя).

В результате перемножения этих элементов матриц получается формула для расчета объема цилиндра.

Рассчитанные объемы аппроксимирующих тел для сверлильного станка в MathCAD:

	0,137 0,046 0,058
V 0 : =
	0,063 0,016 ( 9,44 х 10 - 3 J

Коэффициенты заполнения блоков сверлильного станка:

	f 0,2 1 0,6 0,6
F : =
	0,7
	0,8
	. 0,85 v

Рассчитанные объемы с учетом коэффициента заполнения:

	0, 027 , 0,028 0,035
VV : =	0,044 0,013 ч 8,024 х 10 - 3 v

Массы аппроксимирующих тел:

M

Серия « Естественные и технические науки »

( 214,157 ) ^215,654 269,568 3⁴3,⁹⁸ 98,⁸⁴²

( 62,587 J

Результаты расчета центра масс сверлильного станка с применением MathCAD (координаты в метрах):

X0=0,295

Y0=0,11

Z0=1,453.

Результатом расчета является не только получение конкретных координат центра масс, но и создание шаблона в системе MathCAD, который можно использовать для расчета центра масс станков с подобной компоновкой.

Значительным преимуществом использования данного программного комплекса является его совместимость с простыми графическими редакторами, что позволяет изобразить станок и сделать выполненные расчеты более наглядными. Кроме того, существует возможность теоретического исследования изменения центра масс в зависимости от изменения геометрии и коэффициента заполнения узла.

Поступила 01.09.2014 г.

ВЕСТНИК Мордовского университета | Том 25 | № 1 | 2015

Об авторах :