Использование программных средств поддержки планирования эксперимента для оптимизации параметров генетического алгоритма аппроксимации
Автор: Волков Виталий Витальевич
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Технические науки
Статья в выпуске: 4 (47) т.10, 2010 года.
Бесплатный доступ
Описывается экспериментальная оптимизация скорости сходимости генетического алгоритма аппроксимации, выполненная с использованием специализированных научных программных средств поддержки планирования эксперимента.
Планирование эксперимента, оптимизация, генетический алгоритм, программные средства для научных вычислений
Короткий адрес: https://sciup.org/14249385
IDR: 14249385 | УДК: 519.242:004.023
Текст научной статьи Использование программных средств поддержки планирования эксперимента для оптимизации параметров генетического алгоритма аппроксимации
Введение. В научной и инженерной практике часто возникают задачи планирования эксперимента. Чтобы эффективно спланировать, провести эксперимент, а также обработать его результаты, необходимо воспользоваться специализированными программными средствами (ПС). Обычно применяются MATLAB [1], STATISTICA [2], Design-Expert [3] и др., но перечисленные программные продукты имеют высокую стоимость, закрытый исходный код, а также не все являются кроссплатформенными, что затрудняет их применение на практике. Рассматриваются возможности эффективной комбинации свободных научных библиотек Python и созданного автором ПС EOSupport [4] на примере решения задачи экспериментального поиска оптимальных параметров од- ного генетического алгоритма (ГА) аппроксимации.
Описание исследуемого ГА. Рассматриваемый ГА предназначен для поиска наиболее длинного прямолинейного участка на заданной кривой и аппроксимации его отрезком (рис.1).
В терминологии ГА каждый отрезок – особь, содержащая четыре гена: длина отрезка, угол наклона, координаты x и y центра отрезка. Скрещивание – обмен между двумя особями одним случайно выбранным геном. Мутация состоит в добавлении небольшой случайной величины к одному, произвольно выбранному, гену особи.
Рис.1. Пример результата работы ГА
(точками обозначены границы отрезка, аппроксимирующего наиболее длинный прямолинейный участок кривой)
Постановка задачи. Скорость поиска решения является критичной характеристикой при практическом применении исследуемого ГА. На нее существенно влияют значения множества параметров алгоритма, важнейшими из кото- рых являются вероятности мутации и скрещивания особей. Разные значения этих двух параметров (при фиксированных остальных) приводят к различной скорости сходимости ГА к искомому решению (табл.1).
Таблица 1
Количество итераций ГА, необходимых для достижения решения, близкого к оптимальному, при различных значениях вероятностей мутации и скрещивания
|
№ п/п |
Вероятность мутации |
Вероятность скрещивания |
Кол-во итераций |
|
1 |
0,5 |
0,5 |
24 |
|
2 |
0,85 |
0,3 |
28 |
|
3 |
0,4 |
0,4 |
26 |
|
4 |
0,6 |
0,4 |
25 |
В связи с этим возникает задача поиска оптимальных или близких к ним значений конфигурационных параметров ГА, обеспечивающих наибольшую скорость сходимости алгоритма. Поскольку ГА является разновидностью эвристических алгоритмов, решение данной задачи возможно только методом экспериментального исследования.
Определение условий эксперимента. В качестве управляемых факторов x 1 и x 2 выбраны значения соответственно вероятностей мутации и скрещивания. Другие основные параметры ГА: размер популяции – 2000 особей; отношение размера селекции к размеру популяции – 0,6; используемый алгоритм селекции - турнирный отбор с численностью турнира к = 2 .
В качестве критерия оптимизации, который должен отражать скорость сходимости алгоритма, принято количество итераций, необходимых для получения решения, близкого к оптимальному. Количество итераций берется с отрицательным знаком для приведения к задаче максимизации функции отклика.
Восхождение по поверхности отклика . Поставлен первый полный факторный эксперимент (ПФЭ) в области факторного пространства, обозначенной 1 на рис.2. В каждой точке плана проводилось по 20 параллельных опытов. Полученная линейная модель у = - 26,55 - 3,45 x 1 + 0,8 x 2 , предоставила информацию о направлении роста функции отклика. Выполнено несколько шагов восхождения по поверхности отклика (пунктирная линия на рис.2) в сторону градиента функции. Вычисление коэффициентов модели, проверка ее адекватности, а также расчет траектории восхождения выполнялись средствами ПС EOSupport.
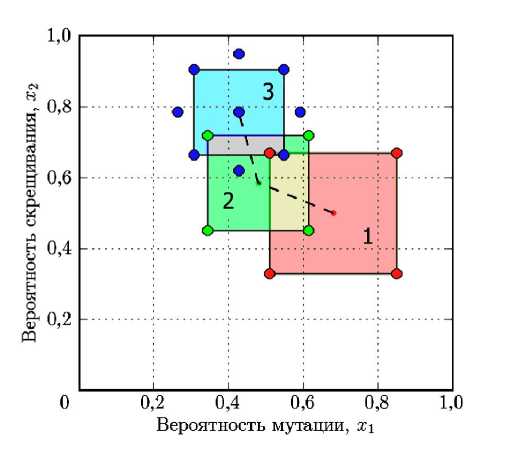
Рис. 2. Расположение областей экспериментов в факторном пространстве
Для автоматизации эксперимента использовались скрипты, написанные на языке Python, с применением библиотеки для работы с матрицами NumPy [5], что позволило производить вычисления со скоростью, не уступающей скорости мощной вычислительной среды MATLAB [6].
В области, обозначенной 2 на рис.2, был поставлен второй ПФЭ и получена новая линейная модель у = - 23,19 - 0,058 х 1 + 0,81 x 2 . Снова были выполнены шаги восхождения по поверхности отклика, в результате чего была достигнута область предполагаемого оптимума.
Планы для всех экспериментов были сгенерированы при помощи ПС EOSupport, которое предоставляет пользователю удобный интерфейс для выбора количества факторов, интервалов их варьирования и типа генерируемого плана эксперимента. На рис.3 представлено диалоговое окно выбора параметров плана.
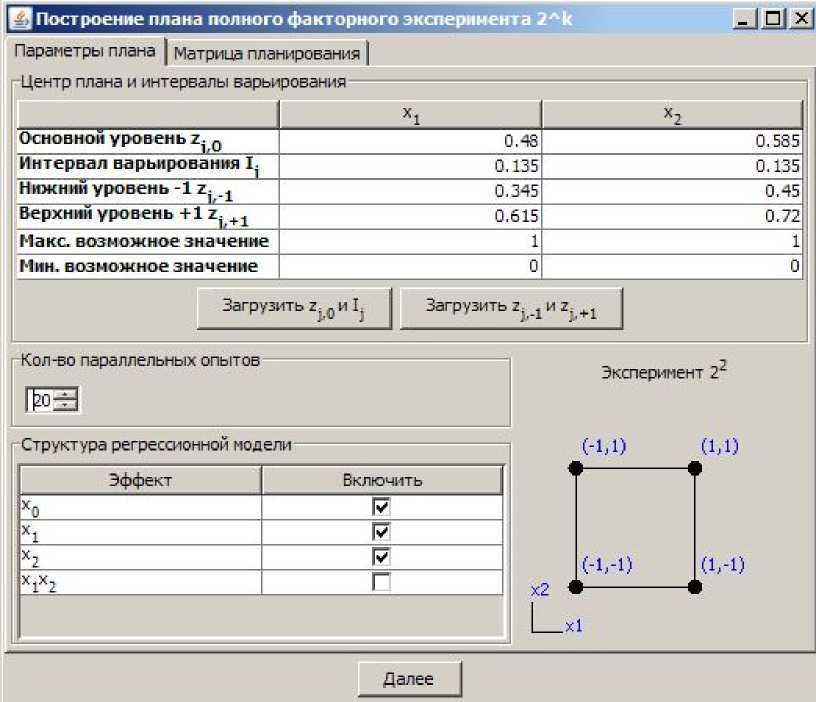
Рис.3. Окно программы EOSupport для подготовки ПФЭ
Описание экстремальной области . В силу того, что достигнутая подобласть факторного пространства (обозначенная 3 на рис.2) практически вплотную приблизилась к допустимой границе, было решено провести заключительный эксперимент на основе центрального композиционного плана (ЦКП). Для повышения точности результата было увеличено количество параллельных опытов до 30. В табл.2 представлена использованная матрица планирования, а также результаты опытов (где y – среднее значение отклика по параллельным опытам).
Таблица 2
Матрица планирования ЦКП и результаты проведенных измерений
|
№ |
x 1 |
x 2 |
y |
№ |
x 1 |
x 2 |
y |
|
1 |
1 |
1 |
–23,73 |
9 |
0 |
0 |
–22,57 |
|
2 |
–1 |
1 |
–21,87 |
10 |
0 |
0 |
–21,2 |
|
3 |
1 |
–1 |
–23,53 |
11 |
0 |
0 |
–23,03 |
|
4 |
–1 |
–1 |
–22,27 |
12 |
0 |
0 |
–23,17 |
|
5 |
–1,369 |
0 |
–27,07 |
13 |
0 |
0 |
–21,33 |
|
6 |
1,369 |
0 |
–24,73 |
14 |
0 |
0 |
–21,7 |
|
7 |
0 |
–1,369 |
–23,63 |
15 |
0 |
0 |
–22,33 |
|
8 |
0 |
1,369 |
–21,77 |
— |
— |
— |
— |
Анализ результатов . Полученная в результате эксперимента ЦКП квадратичная модель после удаления незначимых коэффициентов в кодированных величинах факторов имеет следующий вид:
y = - 22,13 + 0,36 x. - 0,15 x.x, - 1,54 x .2.
2 12 1
График данной модели представлен на рис.4. Все графики данной статьи были построены при помощи специализированной библиотеки Matplotlib [7] для языка Python, имеющей богатые возможности в области визуализации данных.
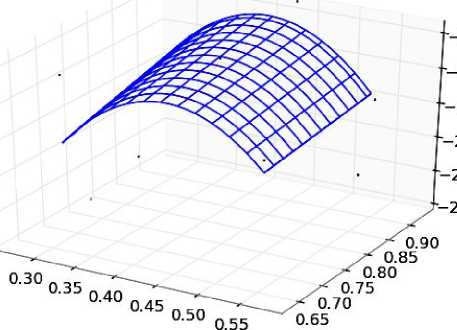
Рис.4. График квадратичной модели поверхности отклика в области в натуральных величинах факторов
Из анализа полученной квадратичной модели следует, что оптимальные значения вероятностей мутации и скрещивания находятся в следующих интервалах: x 1 : 0,35–0,4; x 2 : 0,9–1,0. Серия дополнительных опытов показала, что значение функции отклика в данной области соответствует в среднем 22 итерациям, что является объективным улучшением результатов (табл.1). Выводы. Были исследованы свойства специализированного ГА аппроксимации, определены близкие к оптимальным значения его основных параметров, позволяющие получить наибольшую скорость сходимости. Показана эффективность применения в научной деятельности свободных программных средств на основе языка Python в сочетании с ПС EOSupport.
Список литературы Использование программных средств поддержки планирования эксперимента для оптимизации параметров генетического алгоритма аппроксимации
- MATLAB Statistics Toolbox: Product overview page [Электронный ресурс]. -Режим доступа: http://www.mathworks.com/products/statistics, 2010.
- STATISTICA Data Miner: Overview of software product [Электронный ресурс]. -Режим доступа: http://www.statsoft.com/products/statistica-data-miner, 2010.
- Stat-Ease: Software overview [Электронный ресурс]. -Режим доступа: http://www.statease.com/software.html, 2010.
- Волков В.В. Планирование эксперимента и обработка результатов при помощи программного средства EOSupport/В.В. Волков//Вестник ДГТУ. -2008. -Т. 8. -№ 2 (37).
- Scientific Computing Tools For Python: NumPy: офиц. сайт разработчиков. -Режим доступа: http://numpy.scipy.org, 2009.
- Performance Python: A comparison of weave with NumPy, Pyrex, Psyco, Fortran (77 and 90) and C++ for solving Laplace's equation [Электронный ресурс]. -Режим доступа: http://www.scipy.org/PerformancePython, 2009, нояб.
- Matplotlib: Python plotting: офиц. сайт разработчиков. -Режим доступа: http://matplotlib.sourceforge.net, 2008.
- MATLAB Statistics Toolbox: Product overview page -http://www.mathworks.com/products/statistics, 2010.
- STATISTICA Data Miner: Overview of software product -http://www.statsoft.com/products/statistica-data-miner, 2010.
- Stat-Ease: Software overview -http://www.statease.com/software.html, 2010.
- Volkov V.V. Planirovanie eksperimenta i obrabotka rezul'tatov pri pomoschi programmnogo sredstva EOSupport/V.V. Volkov//Vestn. DGTU. -2008. -T. 8. -№ 2 (37). -in Russian.
- Scientific Computing Tools For Python: NumPy: -http://numpy.scipy.org, 2009.
- Performance Python: A comparison of weave with NumPy, Pyrex, Psyco, Fortran (77 and 90) and C++ for solving Laplace's equation -http://www.scipy.org/PerformancePython, 2009, нояб.
- Matplotlib: Python plotting: -http://matplotlib.sourceforge.net, 2008.