Использование псевдоспектрального метода для поиска траекторий оптимальных по расходу топлива разворотов Международной космической станции

Выполнение ряда задач по программе полета Международной космической станции (МКС) (стыковка и расстыковка с транспортными кораблями, коррекции орбиты и др.) требует периодической смены ориентации станции. Любой пространственный разворот такой многотонной конструкции, какой является МКС, невозможен без интенсивной работы реактивных двигателей (РД) ориентации и, как следствие, значительного расхода топлива.

В настоящее время пространственные развороты МКС проводятся с использованием бортовых алгоритмов служебного модуля (СМ) Российского сегмента (РС) с применением двигателей ориентации РС МКС. Разворот проводится вокруг оси Эйлерова поворота, между текущим и конечным угловым положением МКС. С целью ограничения упругих колебаний конструкции [1] МКС и величин нагрузок на конструкцию [2, 3], при управлении используется шаблон на включения/вы-ключения двигателей Pulse-Train, разработанный американской стороной. При осуществлении таких разворотов расходы топлива МКС зависят от набора используемых двигателей. Например, при развороте МКС на угол ~180° вокруг местной вертикали и при выборе для управления по рысканию и тангажу по одному двигателю СМ, а для управления по крену — по два двигателя корабля «Прогресс», пристыкованного к узлу СО1 МКС, расход топлива составляет ~50 кг, а количество включений двигателей при этом — более 2 000.

Американской стороной также разработан метод выполнения разворотов МКС посредством механизма разгрузки гиродинов Американского сегмента (АС) МКС с использованием РД РС. Двигатели включаются по задаваемой из АС циклограмме. С использованием этого обходного пути проведены развороты МКС под управлением АС по заранее рассчитанной траектории [4]. Оптимальные траектории разворота на угол ~180° вокруг местной вертикали были получены американскими специалистами в 2011 г. с помощью пакета DIDO [5]. При этом было принято, что МКС — твердое тело, управляемое «фиктивными» РД с полностью дросселируемой тягой. Начиная с 2012 г., выполнено несколько десятков таких разворотов МКС.

Российская сторона также проводит работы по созданию оптимальных алгоритмов управления угловым движением МКС. Разработан и введен в состав бортового программного обеспечения (ПО) СМ программный компонент отслеживания заданной траектории. Была численно решена задача оптимального по расходу топлива управления разворотами МКС как упругого тела с использованием РД РС МКС, с учетом импульсной работы РД и ограничений по нагрузкам на упругую конструкцию МКС [3]. При этом были использованы оригинальные алгоритмы оптимизации разработки компании DATADVANCE (г. Москва). Однако для практического применения полученных результатов требуется доработка бортового программного компонента.

Эта работа имеет целью создание алгоритмов, оптимальных по расходу топлива, для осуществления разворотов МКС с использованием РД [3], пригодных для совместной работы с программным компонентом отслеживания заданной траектории. Для оптимизации расхода топлива предлагается использовать гравитационный момент и гироскопические моменты сил, действующие на вращающуюся МКС.

Научная новизна работы заключается в разработанном алгоритме поиска оптимальных траекторий разворота МКС без использования пакета DIDO . Используется псевдоспектральный метод Лобат-то. Этот метод позволяет привести постановку задачи оптимизации к задаче нелинейного математического программирования, которая может быть решена при помощи метода последовательного квадратичного программирования. Практическая значимость работы заключается в значительной экономии топлива и ресурса двигателей ориентации при разворотах МКС по сравнению с используемыми в настоящее время алгоритмами системы управления движением РС МКС.

постановка задачи и цель работы

Основной целью работы является создание оптимального по расходу топлива алгоритма разворотов МКС на большие углы с использованием РД РС МКС и учитывающего влияние окружающей среды. Алгоритм разворота будет использовать моменты сил гравитационного поля Земли и гироскопические моменты от вращения МКС для минимизации общего времени работы двигателей ориентации и сокращения расхода топлива. При решении представленной задачи будем считать МКС твердым телом, тягу РД — непрерывно изменяемой, кинетический момент гиродинов АС зафиксирован относительно инерционной системы координат.

На рис. 1 представлена связанная система координат (ССК) МКС. Она совпадает с орбитальной системой координат [6] (ОСК) в том случае, когда ось Ox _CCК направлена по вектору скорости, ось Oy _CCК направлена от центра Земли, а ось Oz _CCК дополняет Ox _CCК и Oy _CCК до правой тройки векторов.

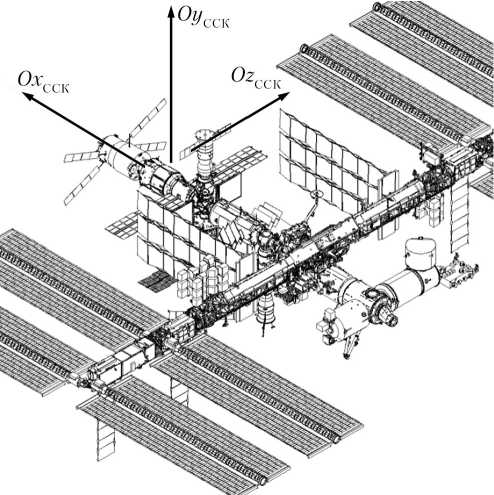
Рис. 1. Связанная система координат (ССК) МКС

Требуется найти управление и траекторию, доставляющие минимум функционалу J (1), при следующих дифференциальных ограничениях, которыми являются кинематическое (2) и динамическое (3) уравнения, а также начальных (4) и конечных (5) условиях:

min J = ∫ ^→ u ^{T →} u dt ;                (1)

q = | (q ° a - a orb ° q);(2)

a = j-1(—[a x ja] + 4d + Tth U);(3)

q(0) = –q0; q(tf) = –qf;(4)

a(0) = 50; a(tf) = af,(5)

где q — кватернион ориентации МКС относительно ОСК; ω ^→ — угловая скорость МКС в ССК; ω ^{→ orb} — орбитальная угловая скорость в ОСК; j — тензор инерции МКС; T ^th — матрица 6×3 моментов сил, создаваемых реактивными двигателями; u ^→ — 6-вектор управления реактивными двигателями; ^→ τ ^d — грав _→ итационный момент сил в ССК; ^– q ₀ и ω ^–₀ — кватернион ориентации и угловая скорость в начальный м _→ омент времени, соответственно; ^– q _f и ω ^– _f — кватернион ориентации и угловая скорость в конечный момент времени, соответственно; t_f — длительность разворота.

Описанный функционал является квадратичным. Он дает следующее преимущество — при решении задачи функция угловой скорости будет иметь непрерывные производные на всем временном промежутке. Такое допущение возможно, так как в существующем бортовом алгоритме траектория закладывается в виде кватернионов ориентации станции относительно ОСК с интервалом Δ t = 55 с по умолчанию и количеством до ста точек.

Матрица управления T ^th и вектор управления u ^→ задаются следующим образом:

T ^th =

T + К	T +P	T +T	T –К	T –P	T –T
x	x	x	x	x	x
T +К	T +P	T +T	T –К	T –P	T –T
y	y	y	y	y	y
T + К z	T +P z	T +T z	T –К	T –P	T z –T

→ u

_u +К _u +P _u +T u –К _u –P

Столбцы матрицы Tth являются векторами моментов сил, создаваемых двигателями. В матрице приняты следующие обозначения: +К — +крен; +Р — +рысканье; +Т — +тангаж; –К — –крен; –Р — –рыска-нье; –Т — –тангаж. Вектор u→ задает тягу двигателей непрерывно на отрезке [0, 1]. В реальности двигатели имеют релейный характер включения, но такое допущение приемлемо, так как бортовой алгоритм отслеживания сейчас использует только оптимальную траекторию разворота, а полученные c таким допущением траектории разворотов МКС дают существенно более низкий расход рабочего тела, чем используемые бортовые алгоритмы.

Гравитационный момент из выражения (3) задается по следующей формуле: →→

Td = Зю. [ j .1.1 ], где j — вектор местной вертикали; юorb — модуль вектора орбитальной угловой скорости; j — тензор инерции МКС.

псевдоспектральный метод лобатто

Оптимизационные задачи могут быть решены численно, с использованием псевдоспектральных методов [7], которые дискретизируют задачу в выбранных точках.

Псевдоспектральный метод Лобатто [8] использует точки Лежандра–Гаусса–Лобатто ( LGL ) и полиномы Лежандра. Пусть

1     d^N

Р =—--—

P N   2 N N ! d т N

(т² -1) N

полином Лежандра степени N на отрезке [т₀, т N ] = [-1, 1]. Точки коллокации LGL т₀ ... т N являются корнями производной полин _. ома Лежандра (6) степени ( N –1) — P_{N –1}, включая крайние точки {–1, 1}. Преобразование к произвольному отрезку [ t ₀, t_f ] производится следующим образом:

⁽ t f ^- t о ^{) т + (} t f ⁺ t о )

t (т) = —------.

Вектор состояния и функцию управления будем аппроксимировать на отрезке [–1, 1] при помощи следующих выражений:

x(t) « xN(t(т)) = Exфг(т);

i = 0

u(t) « uN(t(т)) = Euzфг(т), i = 0

где вектор состояния x ( t ) = [ q ( t ) ω ^→ ( t )] состоит из кватерниона ориентации и вектора угловой скорости; ф i — базисные полиномы Лагранжа, которые имеют следующий вид:

N τ – τ

ϕ _i (τ) = ∏       ^j , ( i = 0, …, N ).

j =0 i j j ≠ i

Значения базисных полиномов удовлетворяют условию Кронекера и определяются следующим образом при разложении по точкам коллокации:

1, если i = k

ϕ(τ ) = δ =                , i k ik 0, если i ≠ k

•

₌          1        (т² - 1)Р_у(т)

^{ф 1} N ( N + T)L_N (т , )     т - т •

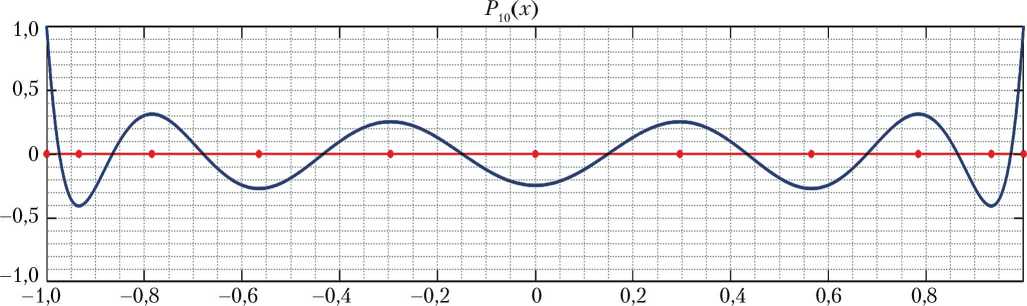
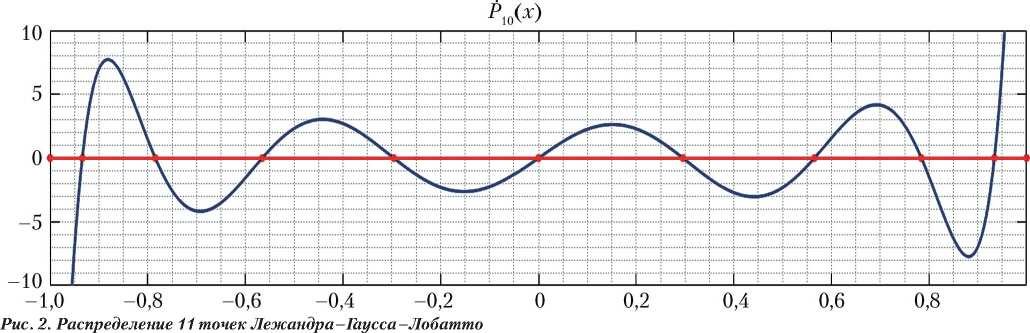
На рис. 2 представлено распределение 11 точек LGL . Как видно из рисунка, точки находятся более плотно к краям отрезка и более редко — к середине. Такое распределение позволяет избежать феномена Рунге [9] — эффекта нежелательных осцилляций, возникающего при интерполяции полиномами высоких степеней. Этот эффект особенно проявляется при интерполяции полиномами на равностоящих узлах.

При подобном разложении производная вектора состояния (7) может быть записана в следующем виде:

.           .               d x ^N d τ          2

Х(^(т)) s хN(t(т^ =            = ~, х k             k       dτ dt τk (tf – t0)

^N                 2 ^N

× ∑ x ϕ(τ ) =          ∑ D x , k = 0, …, N, (9)

i = 0 i i k        (t – t ) i = 0 ki i где dki — матрица дифференцирования Лобатто размерности (N+1)×(N+1), которую можно вычислить по следующей формуле:

PN ( tk )

PN ( ti )( tk – ti )

, если k ≠ i ,

– N ( N + 1)

, если k = i = 0,

N ( N + 1)

, если k = i = N ,

0             в других случаях.

Функционал (1) численно интегрируется при помощи правила Гаусса–Лобатто:

^{f                   (}f ^{- 1} о ) "

J Б ⁽х(О, U(О) dt =--- _о I Б ( х, u ) XD      (10)

1 ₀                                                    2           - - ^{0           1 1 1}

где весовые коэффициенты w_i в точках коллокации вычисляются из следующего уравнения:

^W* ^- N ( N + 1)[ P_N (т - )]²"

постановка задачи нелинейного математического программирования

При помощи описанного выше метода задачу оптимизации можно привести к задаче нелинейного математического программирования (НЛП). Перепишем выражения (1)–(5) при помощи (9), (10) и сформулируем задачу НЛП следующим образом:

( t_f – t ₀) N _{→ →} min J =         ∑ u ^T u w ;

• ₂          i = 0 i i i

• ₂   N      _{1    →→}

• ∑ D q = ( q ω ^→ – ω ^{→ orb} q ), k = 0, ..., N ;

(tf -10) =0 614k 2 k k k k z 2 x E D < = j 1( [er x Jt,] + rd. + Tth u.), (t - T ) /=0 hi к v x L k " kA k k k'1

k = 0, …, N ;

q ₀ = q ₀; q _N = q _f ;

→ ω ₀

→

= ω ₀;

→ ω _N

→ ^{ω –} f ^.

Задача НЛП, описанная выше, была решена численно в среде MATLAB при помощи решателя задач НЛП — функции fmincon [10], входящей в пакет Optimization Toolbox . Для решения задачи использовался метод последовательного квадратичного программирования — при выборе параметра используемого алгоритма задается sqp .

результаты решения оптимизационной задачи

Для решения задачи требуется задать начальное приближение в виде траекторий ориентации и функции угловой скорости. Для начального приближения был взят разворот вокруг оси Эйлера по рысканью на ~180° между начальным и конечным угловым положением МКС. Для разных знаков угловых скоростей в начальном приближении, т. е. для двух направлений разворота, получились различные решения, соответствующие глобальному и локальному минимумам функционала (1). Расходы топлива для всех решений существенно меньше расходов, которые дают существующие бортовые алгоритмы СМ.

При решении задачи было принято считать орбиту круговой. Таким образом, вектор орбитальной угловой скорости в ОСК равен to orb = (0 0 -0,0650) T °/c.

Тензор инерции орбитальной станции примем следующий:

Г126 742 000 -1 859 948 -3 828 571)

J =

-1 859 948

-3 828 571

182 310 992 -808 606 кг-м 2.

-808 606 68 706 280 J

Матрица управляющих моментов, создаваемых реактивными двигателями, равна:

	T → +К T		' 2 532 1147 –205	1 0 0 4004 23	1 0 6 –25 4051	T
	T → +P T → +T
T th =	T → –К	=	–2545	–100	–106	Н⋅м.
	T → –P		–1 196	–4053	–25
	→ T –T		–205	23	4005

Для управления по рысканию и тангажу выбрано по одному двигателю СМ, а для управления по крену — по два двигателя корабля «Прогресс», пристыкованного к узлу СО1 МКС. При каждом включении канала «крен» включается по одному «компенсирующему» РД СМ в канале рыскания.

Были рассмотрены два разворота длительностью 5 400 с. Прямой и обратный развороты назовем условными обозначениями, соответственно: + xV ^ -xV и - xV ^ + xV . Начальные и конечные кватернионы ориентации и угловые скорости этих разворотов соответствуют различным равновесным ориентациям МКС, в которых суммарный момент внешних сил близок к нулю, и управление ориентацией требует наименьших затрат топлива [11]. Для расчета прямого разворота использовались следующие значения начальных и конечных кватернионов ориентации и угловых скоростей:

^–q _{i 1} = (–0,0346 0,0336 0,9988 0,0029);

^–q _{f 1} = (0,9993 –0,0047 0,0260 0,0280);

• ^—i 1 = (-0,0045 -0,0002 0,0649) °/c;

e f 1 = (0,0034 0,0005 -0,0649) °/c.

И, соответственно, начальные и конечные параметры для обратного разворота:

q^– _{i 2} = (0,9993 –0,0047 0,0260 0,0280);

q _{f 2} = (–0,0346 0,0336 0,9988 0,0029);

→

- i ₂ = (0,0034 0,0005 -0,0649) °/c;

^ю f 2 = (-0,0045 -0,0002 0,0649) °/c.

Для каждого из разворотов было получено два варианта решения, найденные в результате различных начальных приближений. Решения были получены для 81-ой точки дискретизации.

Полученные траектории могут быть использованы при управлении ориентацией МКС в специальном режиме, разработанном в рамках данной работы и реализованном в бортовом ПО СМ. В данном режиме МКС осуществляет разворот по некоторой заложенной на борт заданной траектории. Разворот осуществляется под управлением РС МКС, командная ориентация и угловая скорость рассчитываются из упорядоченного набора кватернионов ориентации орбитальной станции относительно ОСК в равностоящих точках вдоль траектории разворота. Интервал между точками, заложенный по умолчанию в ПО СМ, составляет Δ t = 55 с. На каждом вычислительном такте рассчитывается командная ориентация относительно ОСК как результат поворота текущего кватерниона траектории q _j на вектор конечного поворота

→

9 ( t ) =

⁽ t ^- t) _

A t j^

где t — текущее время в секундах; t_j — время в секундах прохождения j -го кватерниона траектории; θ ^→ _{j j +1} — вектор кратчайшего поворота между j -м и ( j +1)-м кватернионами траектории. Командная угловая скорость рассчитывается на каждом такте как сумма векторов орбитальной угловой скорости и 9 /Д t , перепроектируемых на оси ССК.^, Таким образом, система управления движением МКС в данном режиме разворота старается непрерывно отслеживать заложенную на борт траекторию.

На рис. 3–6 представлены решения в виде траекторий ориентации МКС относительно ОСК в углах Крылова в последовательности поворотов рысканье– тангаж–крен и функции вектора угловой скорости в ССК. Красными точками на рисунках обозначены полученные решения задачи нелинейного программирования.

Отметим, что решения, обозначенные «Вариант 1», соответствуют локальному минимуму функционала (1). Для них характерны максимальные отклонения в канале крена на ~20°, а в канале тангажа — на ~40°. Решения, обозначенные «Вариант 2», соответствуют глобальному минимуму. Для них характерны полный переворот в канале крена на 360°, а в канале тангажа — отклонения на ~70°.

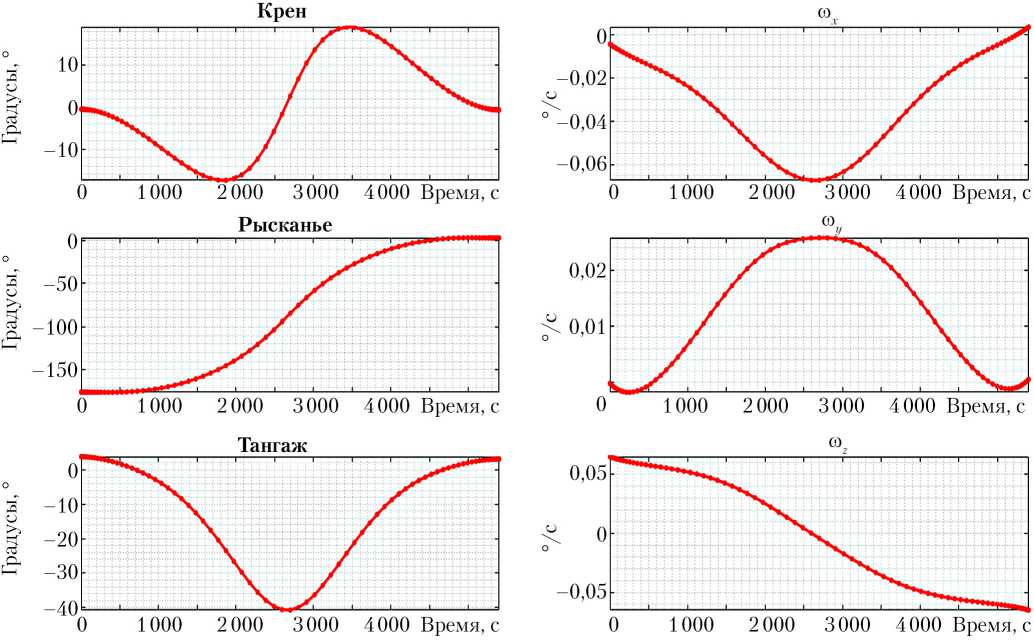
Рис. 3. Прямой разворот +xV ^ -xV. Вариант 1.

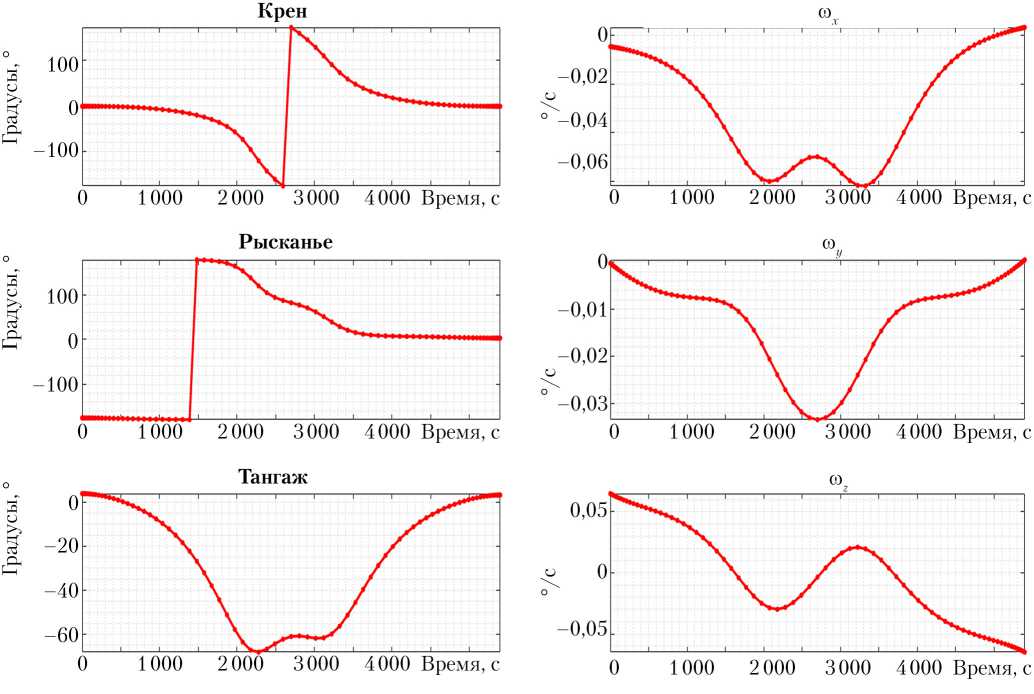
Рис. 4. Прямой разворот +xV → –xV. Вариант 2.

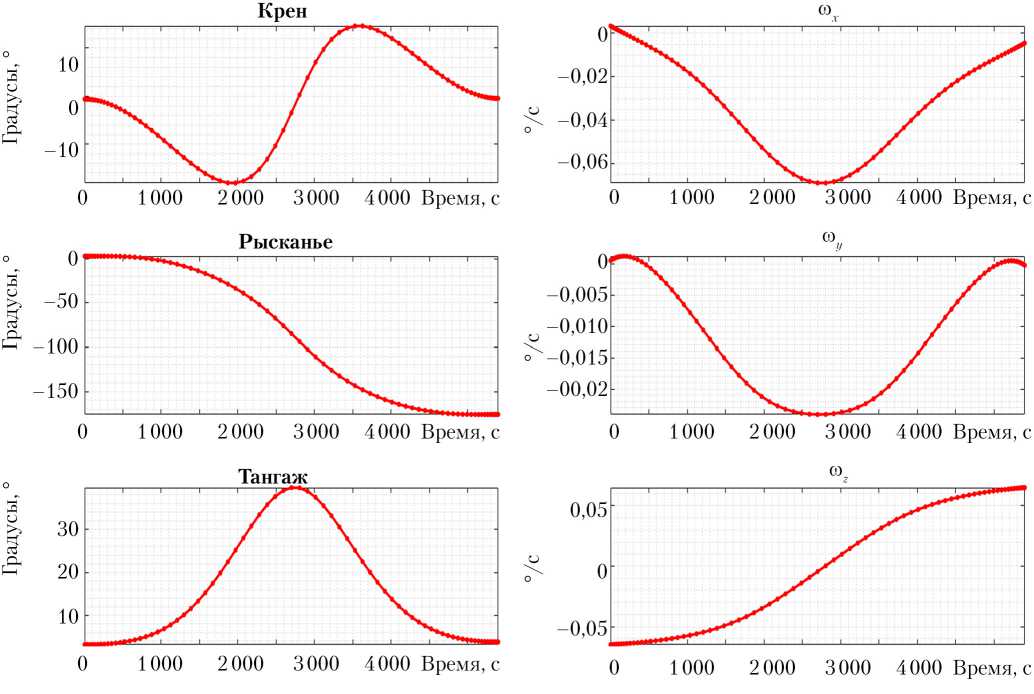
Рис. 5. Обратный разворот –xV → + xV. Вариант 1.

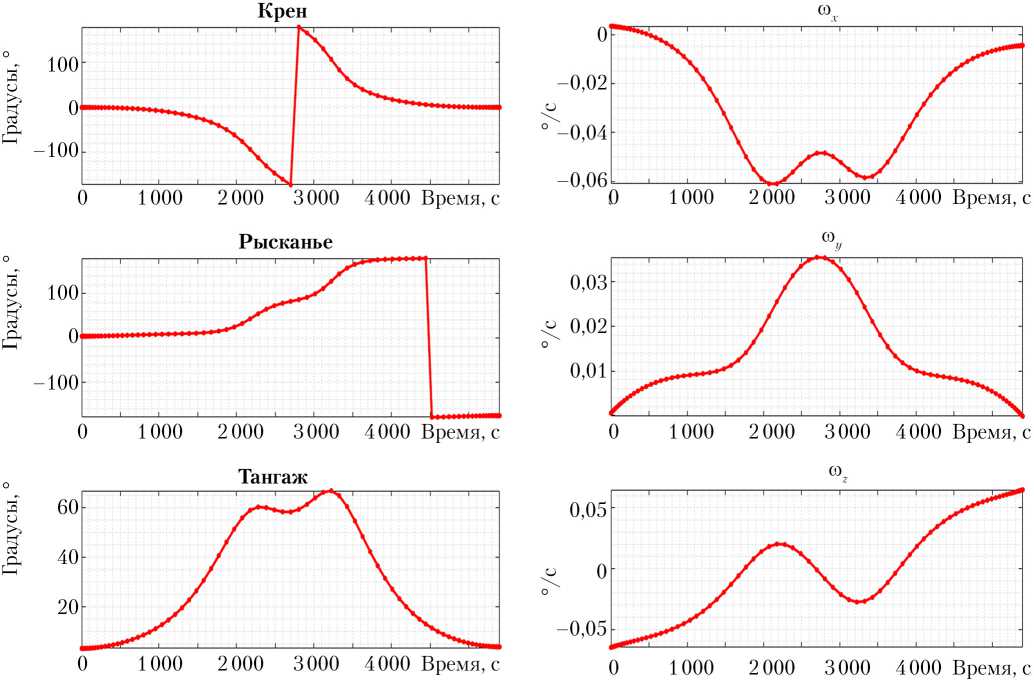
Рис. 6. Обратный разворот –xV → + xV. Вариант 2.

верификация траекторий на наземном комплексе отработки

Для первичной верификации траекторий разворотов было проведено математическое моделирование разворотов МКС на наземном комплексе отработки (НКО) [12]. На НКО установлена летная версия бортового ПО СМ МКС, включающая в себя логику управления в режиме разворота по траектории. Также в ПО НКО реализованы модели динамики и кинематики углового и посту- пательного движений МКС, модели реактивных двигателей, в т. ч. двигателей ориентации, модель датчика угловой скорости, модель атмосферы Земли. Результаты моделирования на НКО, представленные в табл. 1, показали значительную экономию топлива и ресурса двигателей ориентации по сравнению со штатным алгоритмом разворота РС МКС, а также показали результаты лучше, чем текущие алгоритмы АС управления угловым движением орбитальной станции.

Таблица 1

результаты моделирования на наземном комплексе отработки

Варианты	Расход топлива, кг			Количество включений двигателей
	Предложенный вариант	Американский сегмент	Российский сегмент	Предложенный вариант	Американский сегмент	Российский сегмент
+ xV → – xV Вариант 1	7,04	8,02	>40	349	384	>1 000
+ xV → – xV Вариант 2	3,78	4,68		201	287
– xV → + xV Вариант 1	6,40	6,88		309	360
– xV → + xV Вариант 2	2,66	8,08		145	450

Статистическое моделирование

Для вторичной верификации полученных результатов требовалось провести статистическое моделирование, которое представляет собой множественный прогон траекторий на моделирующем комплексе МКС–МА (МКС–модули автономные) [3] при варьировании параметров задачи. В моделирующем комплексе МКС–МА, разработанном одним из авторов данной статьи, реализована бортовая логика управления в режиме разворота по траектории, а также более точная, чем на НКО, модель атмосферы [13]. Вариации задавались по следующим параметрам: начальной ориентации МКС в виде углов Крылова, начальной угловой скорости, тензору инерции МКС, тягам двигателей ориентации и параметрам модели атмосферы — аэродинамическим коэффициентам сил ^→ c и моментов сил m ^→ . Погрешности параметров относительно исходных представлены в табл. 2. Причем, при варьировании одного параметра остальные были фиксированными и равными исходным значениям. Вариация задавалась случайно с равномерным распределением.

Таблица 2

погрешности варьируемых параметров

Параметр		Задаваемые погрешности
Начальная ориентация		±1 °
Начальная угловая скорость		±0,005 ° /c
Тензор инерции		±2%
Тяга двигателей ориентации		±10%
Аэродинамические коэффициенты	→ c	±15%
	→ m	±25%

Было проведено по 200 прогонов моделирования при варьировании каждого из параметров для каждой из траекторий. Таким образом, всего прогонов четырех траекторий было осуществлено 4 000. В табл. 3 и 4 приведена сводная информация по результатам статистического моделирования, которые показали незначительные отклонения от средних значений по расходу топлива и количеству включений двигателей, что не является критичным для использования полученных траекторий, описанных в статье.

Таблица 3

Сводная информация по расходу топлива по результатам статистического моделирования

Варианты	Параметры	Расход топлива, кг
		Минимальный	Максимальный	Средний
+xV ^ -xV Вариант 1	Начальная ориентация	5,70	8,12	6,68
	Начальная угловая скорость	5,39	7,72	6,63
	Тензор инерции	5,46	6,69	6,31
	Тяга двигателей ориентации	5,35	7,34	6,32
	Аэродинамические коэффициенты	5,57	6,80	6,35
+xV ^ -xV Вариант 2	Начальная ориентация	3,93	6,32	4,82
	Начальная угловая скорость	3,97	5,32	4,70
	Тензор инерции	4,26	4,72	4,49
	Тяга двигателей ориентации	3,85	5,06	4,50
	Аэродинамические коэффициенты	4,31	5,05	4,69
-xV ^ +xV Вариант 1	Начальная ориентация	5,70	8,36	6,46
	Начальная угловая скорость	5,65	7,34	6,36
	Тензор инерции	5,70	6,33	6,05
	Тяга двигателей ориентации	5,38	6,71	6,04
	Аэродинамические коэффициенты	5,78	6,37	6,00
-xV ^ +xV Вариант 2	Начальная ориентация	2,75	5,80	3,84
	Начальная угловая скорость	2,92	4,53	3,70
	Тензор инерции	2,81	3,99	3,44
	Тяга двигателей ориентации	2,80	3,99	3,43
	Аэродинамические коэффициенты	3,08	3,86	3,46

Таблица 4

Сводная информация по включениям двигателей ориентации по результатам статистического моделирования

Варианты	Параметры	Количество включений двигателей ориентации
		Минимальное	Максимальное	Среднее
+xV → –xV Вариант 1	Начальная ориентация	376	281	318
	Начальная угловая скорость	357	283	318
	Тензор инерции	317	280	301
	Тяга двигателей ориентации	341	265	302
	Аэродинамические коэффициенты	319	275	304
+xV → –xV Вариант 2	Начальная ориентация	290	217	243
	Начальная угловая скорость	270	208	239
	Тензор инерции	240	214	228
	Тяга двигателей ориентации	263	203	229
	Аэродинамические коэффициенты	259	216	237
–xV → +xV Вариант 1	Начальная ориентация	210	307	245
	Начальная угловая скорость	215	283	242
	Тензор инерции	202	255	225
	Тяга двигателей ориентации	198	251	224
	Аэродинамические коэффициенты	213	238	223
–xV → +xV Вариант 2	Начальная ориентация	161	265	202
	Начальная угловая скорость	171	240	199
	Тензор инерции	164	213	188
	Тяга двигателей ориентации	156	220	187
	Аэродинамические коэффициенты	171	221	194

заключение

При помощи псевдоспектрального метода Лобатто задача оптимального по расходу топлива разворота МКС была приведена к задаче нелинейного математического программирования. Эта задача была решена при помощи решателей, которые используют метод последовательного квадратичного программирования. Были получены четыре гладкие траектории управления разворотом, которые могут быть использованы на МКС при помощи бортового алгоритма слежения за траекторией. Результаты моделирования на наземном комплексе отладки и статистического моделирования показали значительную экономию топлива и ресурса двигателей ориентации при разворотах МКС по сравнению с используемыми в настоящее время алгоритмами системы управления движением РС. Разработанный компонент можно использовать для маневров с другими начальными и конечными условиями, такими как ориентация и угловая скорость, а также с другой продолжительностью маневра. В дальнейшем планируется добавить учет аэродинамических моментов сил [13], а также производить контроль нагрузок на критические элементы конструкции [2], возникающих от работы двигателей ориентации. Результаты работы могут быть использованы при разработке систем управления перспективных орбитальных станций и других космических аппаратов.