Использование регуляризующего алгоритма для определения коэффициентов в задаче оценки собственного состояния термометров сопротивления

В настоящее время одним из актуальных направлений совершенствования средств измерений является поиск методов оценки собственного состояния средств измерения в процессе эксплуатации. Такие средства измерения позволяют повысить метрологическую надежность и точность измерений [1]. К задачам, рассматриваемым в рамках этого направления, относится задача оценки собственного состояния термометров сопротивления.

В предлагаемой работе для этой задачи был построен численный алгоритм решения, основанный на применении метода регуляризации, а также найдены оценки погрешности полученных решений.

Задача оценки собственного состояния была рассмотрена на примере преобразователя температуры с термосопротивлениями из двух различных металлов [2]. 2

Пусть R1 – сопротивление никелевого сенсо- ра температуры, R2 – сопротивление платинового сенсора температуры. При воздействии на сенсоры одинаковой измеряемой температуры зависимость величины их сопротивлений от температуры мож- но представить в виде системы

R 1 — R 01 ( 1 + A i t + A 2 1 ^ + A 4 1^ + A 6 1 ^ j , R 2 — R o2 ( 1 + B i t + B 2 1 ^ ^_ 100 B 4 1 ^ + B 4 1 ^ j ,

где t - температура; R ₀₁, { A m } 6 - коэффициенты г-» 1 тч Г тч 1 4

никелевого сенсора [3], а R₀₂ , { B l } 1 - коэффициенты платинового сенсора [4].

В то же время непосредственно измеряемыми в процессе эксплуатации величинами являются сопротивления R 1 и R ₂. Поэтому возникает необходимость в решении обратной задачи, позволяющей восстанавливать значения температуры по результатам измерения сопротивлений. Одним из ключевых моментов в решении этой задачи является определение значения коэффициентов, характеризующих зависимость температуры от сопротивлений.

Решение этой задачи состоит из нескольких этапов. На первом этапе проводят калибровку преобразователя, в процессе которой осуществляют эксперимент, измеряя сопротивления R 1 , R ₂ и температуру t _этал с помощью эталонного термометра. На этом этапе находят вид зависимости температуры от сопротивлений и определяют величины коэффициентов в этой зависимости. На втором этапе в процессе поверки для каждого сенсора восстанавливают значения температуры t _восст , используя полученные результаты, и оценивают величину уклонения t _восст от t _этал. Но поскольку в процессе эксплуатации результаты измерения эталонного термометра неизвестны, то возникает необходимость в третьем этапе, на котором осуществляют выбор критериев, позволяющих провести оценку собственного состояния средства измерения.

Нахождение коэффициентов в процессе калибровки, восстановление значений температуры по результатам измерения сопротивления, выбор критериев, позволяющих оценить собственное состояние термометра сопротивления в процессе эксплуатации, является целью данного исследования.

Постановка задачи

На первом этапе происходит построение математической модели задачи на основе измеренных величин R 1 , R ₂ и t _этал. Пусть проведено n измерений. Обозначим t k - отдельное измерение t этал ; k = 1, n ; R 1 к - сопротивление первого материала, измеренное при температуре t k , а R _{2 k} -сопротивление второго материала.

Так как по условиям эксперимента измерения сопротивлений проводились при одинаковых температурах, то в качестве математической модели, характеризующей зависимость температуры от сопротивления, рассмотрим систему

и связанное с ней уравнение

A m R mk ⁺ A m - 1 ^R 1 m ^{1 +} A m- R R m 2 ⁺ ... ^{+ A} 1 R ik ⁺ A 0 =

= B i R 2 k + B i - 1 R 2 ^{- 1} + B i— RR 2 ^{- 2} + ... + BR 2 k + b o .    (3)

Проблема заключается в том, что априори неизвестны не только коэффициенты Ai, Bj, но и степени m и l. Кроме того, нам неизвестны точные значения tk, вместо них измерены значения Т^™ и уровень допустимой температурной погрешности 8. В этих условиях необходимо определить степени полиномов m и l, коэффициенты Ai и Bj, а также, используя систему (2), необходимо по восстановленным коэффициентам и степеням найти значения измеренной температуры изм                                       этал tk и оценить её отклонение от Tk .

Стандартные методы решения систем алгебраических уравнений оказываются неприемлемыми для решения (2), поскольку не определены степени полиномов и правая часть системы (2) известна приближенно. Кроме того, учитывая связь (1), имеем, что малые погрешности при измерении t_k , приведут к возникновению погрешностей R ₁ , R ₂ , что в свою очередь неизбежно приведет к существенным отклонениям t™ в задаче (2),(3), то есть решение обратной задачи будет неустойчивым относительно погрешности исходных данных. Поэтому для решения системы (3) необходимо построить регуляризующий алгоритм.

Численный метод решения задачи определения коэффициентов в задаче оценки собственного состояния

Введем следующие обозначения. Пусть опе раторы P1 и Р2 определены матрицами:

R m

R m ^{- 1}

R 11 1 )

п m mm -1 р = R 12 R 12

n m  m ^{- -1}       t?   1

V ^R 1 n ^R 1 n ......^R 1 n 1 7

	m R 21	P m -1 R 21 .	...R 21	1 1
P 2 =	m R 22	n m -1 R 22 .	. R 22	1
	m V R 2 n	n m - 1 R 2 n ..	■. R 2 n	1 J

T 8 = ( t    ; T ₂    ; . T n ) . Тогда система (2)

примет вид

I P 1 u = T 5 ,

IP2 v = T5, а уравнение (3) преобразуется к виду

P 1 и = P ₂ v .

Для решения задачи (5), (6) построен численный метод, схема которого имеет следующий вид.

Шаг 1. Находим степени полиномов, стоящих в левых частях системы (5). Пусть M – максимальное число линейно независимых столбцов матрицы P ₁ , а L – матрицы P ₂ . Если расширенные матрицы

( P1 |T ₅) и ( P₂ |T ₅) имеют тоже число линейно неза-

висимых столбцов, то из курса линейной алгебры [5] известно, что система (5) будет иметь решение в том случае, когда m = M и / = L .

Шаг 2. Для получения решения I и «1 ; v «2 ) сис-

темы (5), устойчивого относительно погрешностей исходных данных, используем регуляризующий алгоритм, основанный на введении стабилизирующего функционала. Согласно такому подходу [6] вместо системы (5) рассмотрим систему

P * P 1 и + « 1 и = P ^ T ₅ , « 1 >  0, _ P ₂ * P ₂ v + « ₂ v = P ₂ * T ₅ , , « 2 >  0,

<

**

где P ₁ и P ₂ – матрицы, сопряженные к P ₁ и P ₂

соответственно, а « 1 , « ₂ - некоторые параметры

регуляризации.

Для выбора параметров регуляризации ис-

пользуем принцип невязки, согласно которому в

качестве параметров регуляризации рассматривают решения уравнений [7]:

и « - ( P; P +« ! E f¹ T ₅

v «2 - ( P 2 P 2 + « 2 E ) "* T §

57«Т’

«Ч

где E – единичная матрица.

Такой подход к выбору параметров позволяет не только найти устойчивые решения системы (5), то есть восстановить коэффициенты в системе (2), но и получить гарантированную оценку погрешности восстановленных коэффициентов [7].

Шаг 3. Для оценки погрешности найденных коэффициентов используем результаты, полученные в работе [8]. Тогда А 1 - величина погрешности определения коэффициентов первого материала и А ₂ - второго материала удовлетворяет нера-

венствам:

2 ^/«1

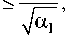
2 7а2"

, 5

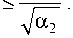
Полученные оценки являются неулучшаемы-ми по порядку.

Шаг 4. Подставляя и «1 = ( A m¹ ; A m «-1 ; ^ A «1 ) и v « ² = ( B «²; B “²f,... B о ² ) в систему (2), найдем значения T ^изм1 = ( t ™; t ™;... t ™) для никеля и T изм ² = ( t изм ; t изм ; ^ t и з м ) для платины. Вычислим экспериментальную оценку погрешности А 1 k и А ₂ k для каждого металла по правилу

Л _А т->изм т-’этал Т т->изм <гэтал т i

1 k = ^T 1 k ^{- T}k , ^А 2 k = ^T 2 k ^{- T}k , ^k = 1, n .

Такой подход позволит оценить погрешности восстановленных температур [2].

Шаг 5. Так как в процессе эксплуатации значения tkэтал неизвестны, то подставив «1 ( ла1. Л«1 . л«1\        «2 / г>«2. г>«2. г>«2 \ и 5 =( Am; Am-1;-Ai) ) и v 5 =( Bl ; B/-1;^B0 ) в уравнение (6), оценим погрешность восстановленной температуры Tизм следующим образом. Для любого k найдем

^А k = |( A m R mk ⁺ A m -1 R 1 m ^{1 + +} A 1 R I k ⁺ A 0 ) ^-

- ( B / R 2 k + B / -1 R 2 -¹ + + B 1 R 2 k + B 0 )| .

Рассмотрим величину min А k

А- — ^k .                       (10)

max А _k k

Если имеет место неравенство 0,1 < А < 1, то погрешность прибора находится в заявленных пределах. Если неравенство нарушено, то погрешность прибора вышла за заявленные пределы.

Результаты вычислительного эксперимента

С целью проверки эффективности построенного алгоритма и получения экспериментальных оценок погрешности температуры были проведены вычислительные эксперименты как для серии модельных примеров, так и на основе экспериментальных данных.

Пример 1. В проведенной серии вычислительного эксперимента рассматривались модельные функции при t ^этал е [ - 50;250 ] °C. Значения сопротивлений вычислялись по формуле (1). В качестве значения t_k ^этал рассматривались значения равномерно распределенной случайной величины t_k . Интервалы распределения согласовывались с величинами допуска для каждого сенсора [3, 4].

На рис. 1 изображены величины погрешностей для восстановленных температур при условии, что t_k ^этал находится в пределах соответствующих классов допуска. Величина погрешности, определяемой формулой (10) составляет А = 0,17901.

На рис. 2 изображены величины погрешностей для восстановленных температур при условии, что t_k ^этал находится вне пределов соответствующих классов допуска. Величина погрешности, определяемая формулой (10), составляет А = 0,010672.

Пример 2. В проведенной серии вычислительного эксперимента рассматривались модельные функции при T этал е [ - 50;250 ] . В качестве значения t_k ^этал рассматривались значения равномерно распределенной случайной величины t_k . Интервалы распределения согласовывались с классами допуска для каждого металла.

Величины сопротивлений вычислялись по формуле (1) и в полученные значения вносились дополнительные погрешности h1 и h2 для каждого материала соответственно. Эти погрешности определялись как значения равномерно распределенных случайных величин на интервале [- H; H ].

На рис. 3 изображены величины погрешностей для восстановленных температур при условии, что T_k ^этал выходит за пределы соответствующих классов допуска. Величина погрешности, определяемая формулой (10), составляет А = 1,001204.

Пример 3. В проведенной серии вычислительного эксперимента рассматривали с ь экспериментальные данные. На рис. 4 изображены велич и ны погрешностей восстановленных температур для данных, полученных при провед е нии экспе-

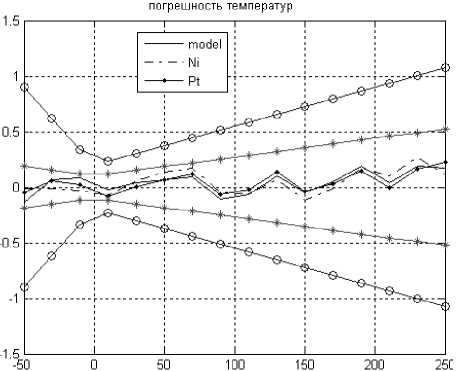
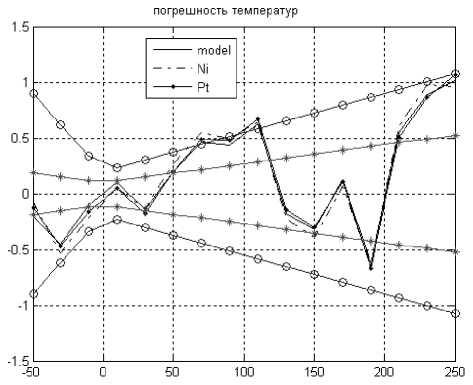
Рис. 1. Графики погрешности температур. Линии    Рис. 2. Графики погрешности температур. Линии

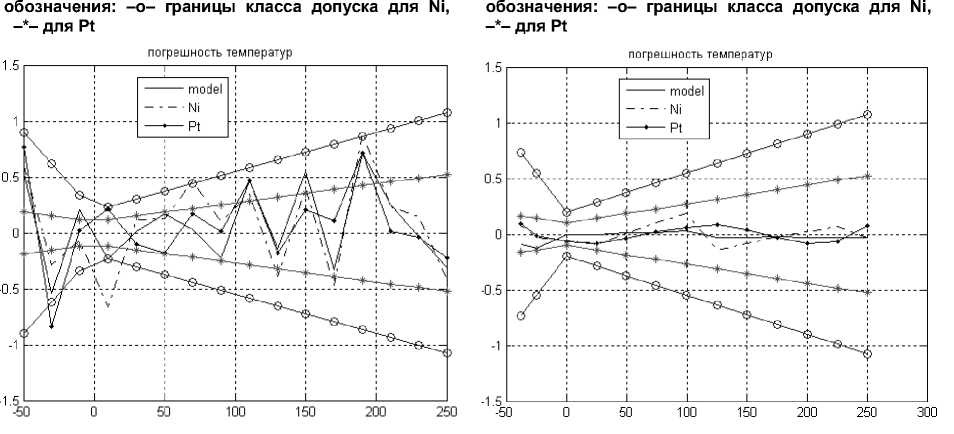
Рис. 3. Графики погрешности температур. Погрешности сопротивления h ₁ и h ₂ выбраны из [ - 0,1; 0,1 ] . Линии обозначения: -о- границы класса допуска Ni, –*– для Pt

Рис. 4. Графики погрешности температур для экспериментальных данных. Линии обозначения: –о– границы класса допуска для Ni, –*– для Pt риментов. Провод тока и провод напряжения с одной стороны термосопротивления были закорочены шунтирующим магазином сопротивлений со стороны измерительного преобразователя. Величина погрешности Δ, определяемая соотношением (10), составила 0,001962.

По результатам, полученным при проведении вычислительного эксперимента, можно сделать вывод о том, что предложенный регуляризующий алгоритм позволяет восстанавливать значения температур с требуемой точностью. Этот алгоритм является устойчивым относительно температурных погрешностей и не зависит от того, находиться ли измеряемая температура в пределах требуемого класса допуска или вышла за его пределы.

Более того, предложенный подход позволяет выделить критерии, на основании которых можно проводить оценку собственного состояния средств измерения.

Заключение

Проведенный вычислительный эксперимент показывает, что использование регуляризующего алгоритма для определения коэффициентов в задаче оценки собственного состояния термометров сопротивления позволяет получать устойчивые решения, восстанавливать коэффициенты и температуру по результатам измерения сопротивления с достаточной точностью. Кроме того, предложенный подход может послужить основой для оценки погрешности восстановленной температуры, а также для выбора критериев, позволяющих прово- дить оценку собственного состояния средств измерения.