Использование рекуррентной процедуры метода наименьших квадратов для определения параметров линейных динамических объектов

При эксплуатации систем автоматического управления параметры объекта могут быть известны не точно, либо они могут меняться со временем. Поэтому определение параметров объекта в процессе работы системы с целью настройки параметров регулятора для более качественного функционирования объекта является актуальной задачей [1–6]. Одним из путей решения данной задачи – это воздействие на систему тестовым сигналом, оптимальным в некотором смысле. В работах [7–9] поиск оптимального сигнала, воздействующего на динамическую систему, реализуется посредством использования информационной матрицы Фишера. Авторы работы [10] описывают процедуру идентификации параметров в ходе синтеза управления по выходу для систем второго порядка с помощью решения системы нелинейных алгебраических уравнений. При этом параметры объектов предварительно были получены в специальных тестирующих экспериментах. В работе [11] анализируется выбор норм невязок и их комбинаций при параметрической идентификации моделей. Параметрическая идентификация основана на включении в модель параметров и их подборе из условия минимизации нормы невязки. В [12] предложен критерий, являющийся обобщением метода наименьших квадратов, который позволяет получать сильно состоятельные оценки параметров линейных динамических систем дробного порядка с ошибками в переменных и в

условиях отсутствия информации о законе распределения.

В данной работе рассматривается динамический объект, который в общем виде можно выразить следующим образом:

x k + 1 = ^{Ф x} k + ^u k ⁺ w k ,

Ук+1 = Hxk+1 + vk+1, где xk+1 - вектор состояния, uk - вектор управления; wk - вектор возмущения, yk+1 - вектор измерения, vk+1 - вектор ошибки измерения, Ф - матрица состояния, Г - матрица возмущения, ¥ - матрица управления, H - матрица наблюдения, Q – неотрицательно определенная матрица ковариации вектора возмущения, R – положительно определенная матрица ковариации вектора ошибки измерения. Параметры 0 = (01,02,...,0n), которые требуется определить, находятся в матрицах Ф(0\ ^(0"). Предлагается рекуррентная схема метода наименьших квадратов для определения параметров линейных динамических объектов в установившемся режиме, то есть все переходные процессы закончились.

1. РЕКУРРЕНТНАЯ СХЕМА МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ

Для определения параметров 0 = (0,02,..., 0п)т объекта y = xт 0 в случае векторного входа x = (x 1,x2,..., xn)т и скалярного выхода y наиболее типичным алго- ритмом оценивания неизвестных параметров является рекуррентный алгоритм метода наименьших квадратов [13–15]:

Л         Л

⁰ N + 1 = ⁰ N ^{+ K} N + 1 ⁽ y N + 1

т Л xN+10N )

,

KN+1 = PNxN +1 ( 1 + xN+1 PNxN+1) , тТ

Р =(Т-Р  x^{N + 1} x^{N + 1} \P

^P N + 1 ⁽ I ^P N       Tn      ) P N ,

^{1 +} x N + 1 P N x N + 1

где K N + 1 - вектор-столбец коэффициентов усиления размером n , P N , P N + 1 - матрицы, обеспечивающие оценку дисперсии ошибки оценивания, вычисленные по результатам N и N + 1 измерений соответственно, I – единичная матрица размером n х n , y_{N + 1} - скаляр, 0_N , 0_{N + 1} , x_{N + 1} - векторы-столбцы размером n . Моделирование рекуррентной процедуры метода наименьших квадратов организовано в виде блоков нескольких уровней. Каждый блок соответствует определенной формуле, входящей в алгоритм оценивания неизвестных параметров. Данный способ моделирования позволяет компактно отразить весь процесс определения параметров объекта. Более подробно ознакомиться с порядком формирования рекуррентного алгоритма наименьших квадратов в среде Simulink можно в работах [14, 15].

2. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ АЛГОРИТМА ОПРЕДЕЛЕНИЯ ДИНАМИЧЕСКИХ ПАРАМЕТРОВ

В общем случае представление используемой процедуры является очень большим и сложным, поэтому она иллюстрируется на модели (рис. 1), которая может быть использована при описании перевернутого маятника, Эта модель часто используется при анализе и синтезе систем управления [9, 16, 17] .

Для примера, изображенного на рис.1, была построена модель в пространстве состояний:

⁴ x k +1^{Л x2} + 1

x k + 1

у 4

V x k + 1 у

4 0   d0

1  1 - d0

0   01

V 0    011

+

4 ad + c

—ad + a + b

01 a v 01 a

Uk +

V

• — (ad + c) '

( ad — a — b )

• ^{— (1 +} . )

( 0 2 — 0 1 a ) J

5:

wL •

< J

^{4 x} 1' x k „ 3 x_k ³ X ⁴

Vxk J

+

У к + 1 = ^{(0 0 0} 1) x k + 1 ⁺ v k + 1

где a = 135, b = - 216,25, c = 87,5, d = 0,375. Осуществив подстановку указанных значений, получим следующее описание объекта в пространстве состояний:

x k + 1 x k + 1

x k + 1

у 4

V x k + 1 J

+

V ⁰

4 138,125

—

V

131,875

135 0 ₁

0,375

0,625

A

uk +

⁴ w k + 1

<1

— 138,125

131,875

— 1 + 135 0 1

0 ₂ — 135 0 1

A

w k + 1

A

J

x

x

' k

' k

x k ³

X ⁴

Vxk J

+

,

135 0 _{1 J}

V w+1J

y k + 1 = ^{(0 0 0} 1) x k + 1 ⁺ v k + 1

При рассмотрении данного примера приняты следующие базовые значения для 0 1 , 0 ₂ : 0 1 = 0,005 , 0 ₁ = 2,05 . Для базовых значений 0 1 , 0 ₂ динамический объект принимает вид:

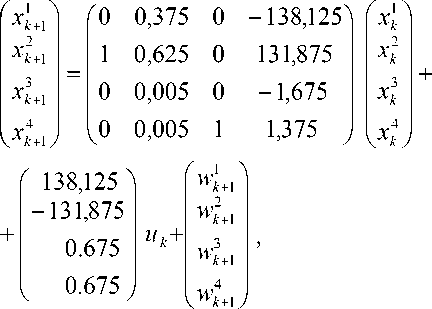
y k + 1 = ^{(0 0 0} 1) x k + 1 ⁺ v k + 1 .

В среде Simulink выполнено моделирование динамического объекта (рис. 2).

На рис. 3 показана реакция системы, если входной сигнал - единичная ступенчатая функция.

При подаче на вход тестового сигнала в виде единичной ступенчатой функции имеем сле-

дующие оценки параметров: 0 1 = 0,0003487 , 0 ₂ = 1,053 .

Во многих случаях в качестве тестового воздействия подают на вход периодический сигнал типа меандра. В данной работе выбран входной

сигнал типа меандра с периодом T = 8 и с ам-

плитудой, равной единице (рис. 4). В качестве начального значения матрицы P принято сле-

дующее значение: Р ₀ =

4 1,5 0,4 )

I .

V 0,4 1,5 J

На рис. 5 показан выходной сигнал системы, если в качестве тестового сигнала используется сигнал типа меандра.

После N = 100 измерений получены оценки параметров 0 = ( 0 1 , 0 ₂) : 0 1 = 0,003592 , 0 ₂ = 1,77792 . Результаты моделирования даны для случая, когда присутствуют шумы про-

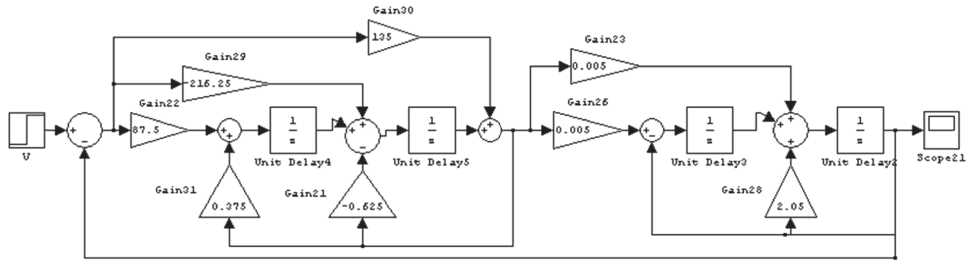
Рис. 1. Модель объекта

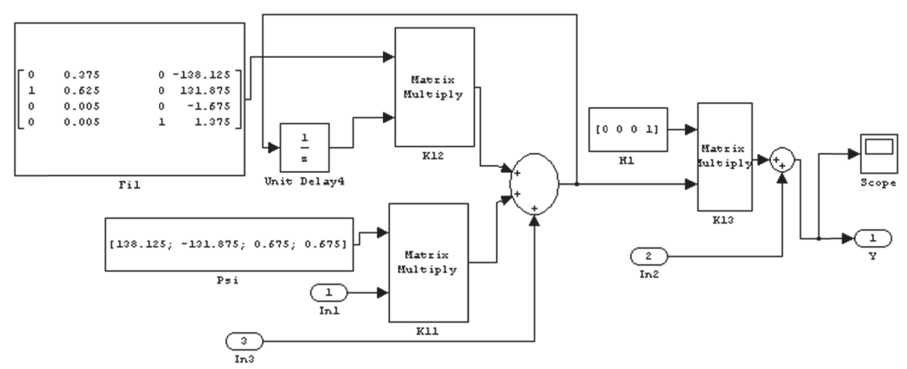
Рис. 2. Моделирование объекта

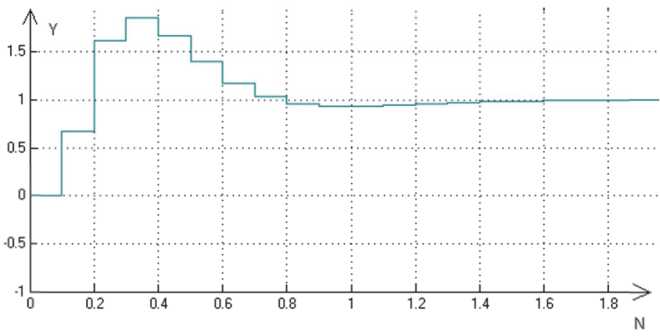
Рис. 3. Реакция системы на входной сигнал в виде единичной ступенчатой функции

цесса w с нулевым средним m и дисперсией g ² = 0.005 , что соответствует погрешности измерений в пределах 5% - 7%. Ниже приводятся значения коэффициента усиления K и матрицы P : K = [ - 0,0006536; - 0,09276] , P = [0,00005062 0,003052; 0,003052 0,5497]

. При увеличении числа измерений N = 200 оценки параметров 0 = (0 1 , 0 2 ) сходятся к базовым значениям: 0 1 = 0,004 , 0 ₂ = 1,911 . На рис. 6 приведен график поведения коэффициента усиления.

Элементы матрица P   при увеличении измерений также   изменяются:

P = [0,00002786 0,001951; 0,001951 0,3425] . Отметим, что наблюдается довольно быстрая сходимость алгоритма и невысокие значения дисперсии оцениваемых параметров. Многократное вычисление параметров объекта при различных параметрах шумов подтверждают работоспособность алгоритма и его реализацию в среде Simulink.

ЗАКЛЮЧЕНИЕ

В среде Simulink выполнено моделирование динамической системы на примере объекта четвертого порядка, осуществлено формирова-

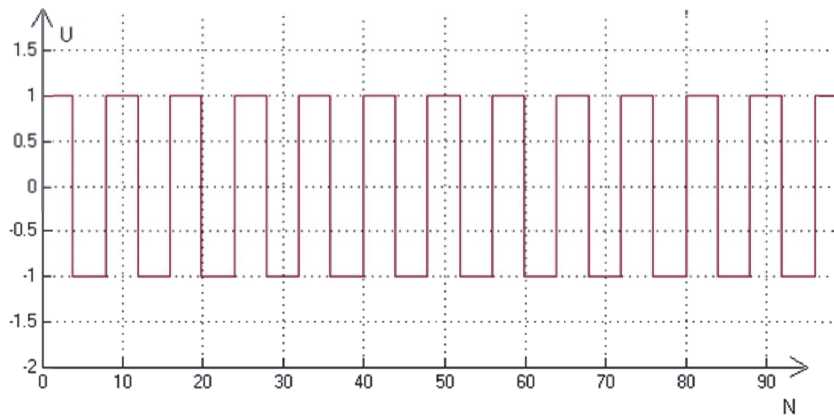
Рис. 4. Входной сигнал типа меандра с периодом T = 8

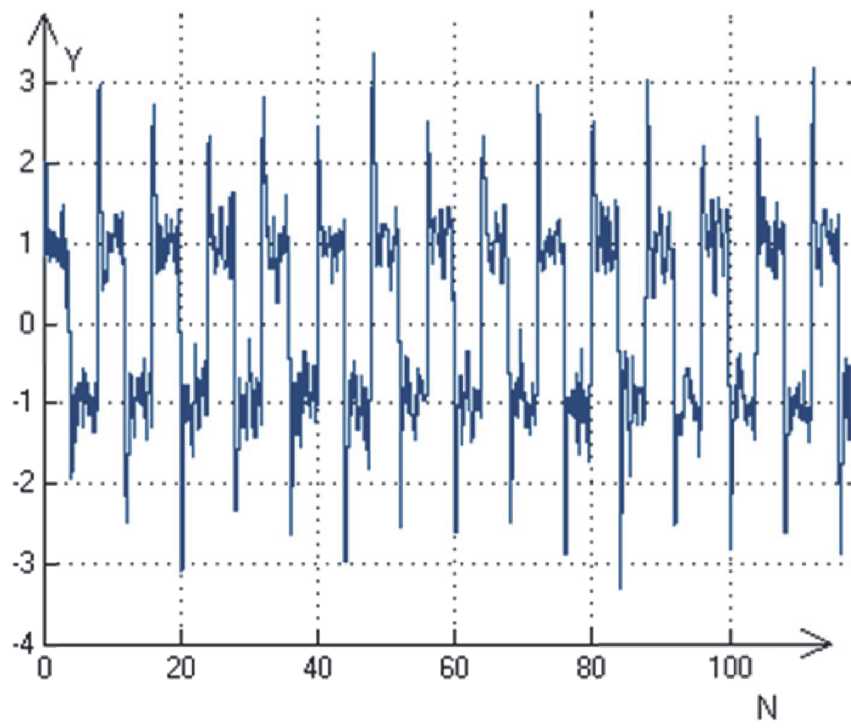
Рис. 5. Выходной сигнал

ние уравнений рекуррентного метода наименьших квадратов. Приводятся графики входного и выходного сигналов. В данной работе используется входной сигнал типа меандра. Приводятся результаты определения динамических параметров. Использование итерационных схем определения параметров в практических исследованиях является важной задачей, поскольку алгоритмы идентификации должны осуществлять мониторинг любых изменений свойств системы за определенный промежуток времени. В дальнейшем предполагается использование рекуррентных методов оценивания для определения параметров многоканальных динамических объектов более высокого порядка с большим числом параметров.

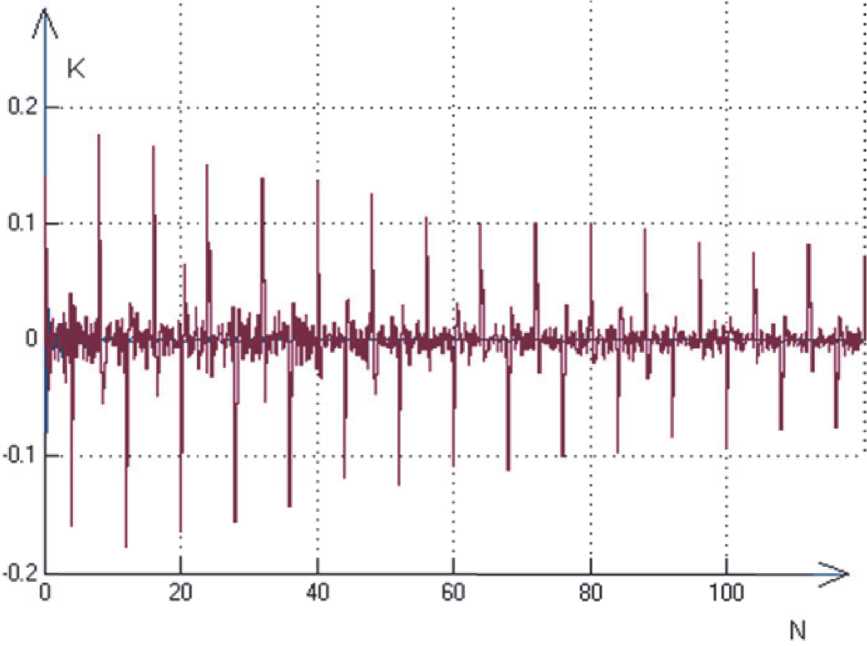
Рис. 6. Поведение коэффициента усиления K