Использование современных информационных технологий в экономико-математическом моделировании

Одним из приоритетов в реализации экономических реформ является создание малых предприятий, занимающихся переработкой местного сырья и производством конкурентоспособной готовой продукции. Оптимальное принятие решений в условиях неопределенности имеет важное значение для эффективной работы существующих предприятий.

Не секрет, что основные достижения научно-технического прогресса должны применяться к производству и создавать новые возможности для реализации следующих основных задач:

• >    экономия (экономия времени, сырья, топлива, электроэнергии и т. д.);

• >    упрощение производственных процессов, упрощение труда;

• >    изменить содержание и характер труда;

• >    повышение     социально-экономической     эффективности

производства.

Все вышеперечисленные задачи решаются путем моделирования экономических процессов и поиска оптимальных решений для них.

Предположим, что граничные условия задачи оптимального программирования состоят из системы линейных уравнений и неравенств, то есть задача оптимального программирования задается в следующем виде.

Мы знаем, что целевые функции задач линейного программирования и функции, включенные в условия ограничения, будут состоять из линейных функций искомых неизвестных. Предположим, нам нужно найти минимум или максимум, который удовлетворяет системе предельных уравнений или неравенств функции, зависящей от n переменных, то есть х = (x1, x2, ..., xn).

Предположим, что m разных видов сырья используется для производства n разных продуктов.

Давайте введем следующие определения:

• b i - доступное количество различного сырья;

Aj (j = 1..n) - тип продукта;

• a ij- количество потребляемого мной различного сырья на единицу продукцииj;

• c j - доход от различных единиц продукта j.

Если мы обозначим количество продуктов, которые будут произведены х j , математическая мо де ль задачи бу де т следующей:

X j > 0, j = 1, n    b i > 0, i = 1, m                           (1)

X^a ij X j ^A j ,                          (2)

F- max = I i=i C i^xi

Первая формула математической модели представляет собой ограничения на искомые количества в экономическом смысле, которые возникают из-за количества ресурсов, необходимости удовлетворения определенных требований, технологических условий и других экономических и технических факторов. Второе условие - это условие, что переменные, то есть искомые величины, не являются отрицательными. Третий называется целевой функцией и представляет отношение искомой величины.

Есть несколько различных способов решить эту проблему линейного программирования. Однако с помощью современных компьютерных технологий эта проблема очень легко решается.

Для этого рассмотрим следующую проблему, которая сводится к проблеме линейного программирования.

Фабрика производит два вида швейных изделий A и B. В производстве продукции используются три разных типа материалов N1, N2, N3. Склад имеет запас 15 м из материала 1, 16 м из материала 2, 18 м из материала 3. А использует 2м от N1, 1м от N2, 3м от Nz для производства продукта. В-использует 3м от N1, 4м от N2, 0м от N3 для производства продукта. A-прибыль с одной единицы продукта составляет 10 тысяч сумов, В - прибыль от продукта составляет 5 тысяч сумов.

Необходимо составить производственный план, чтобы завод получал максимальную прибыль. Давайте создадим математическую модель задачи:

Следующие шаги используются для решения этой проблемы с помощью инструментов электронных таблиц. На новом листе:

• 1.    В ячейках B1: B3 введите числа 15, 16 и 18 дневной резервной суммы соответственно.

• 2.    В ячейки B11 и C11 вводим нули с начальными значениями неизвестных значений х 1 и х 2 . Эти значения изменятся в результате будущих расчетов.

• 3.    В ячейках B3: C5 указана сумма затрат на сырье для продукта.

• 4.    В ячейки B17:B19 введите формулу для расчета количества потребляемого сырья по типу продукта.

В17=СУММПРОИЗВ(B3:C3;B11:C11),

B18=СУММПРОИЗВ(B4:C4;B11:C11),

B19= СУММПРОИЗВ(B5:C5;B11:C11).

• 1.    В ячейку C13 введите формулу для целевой функции: =B6*B11+C6*C11.

• 6.    В ячейках C17: C19 вводится количество товара на складе.

• 7.    C помощью команд Данные / Поиск решения откроется диалоговое окно. “Поиск решения”. Если функция недоступна в рабочей области, ее можно создать, активировав раздел «Настройки» / «Надстройки» / «Перемещение» / «Поиск решения».

• 8.    Адрес оптимизированной ячейки C13 отображается в поле Оптимизировать целевую функцию. (Рисунок 2).

  

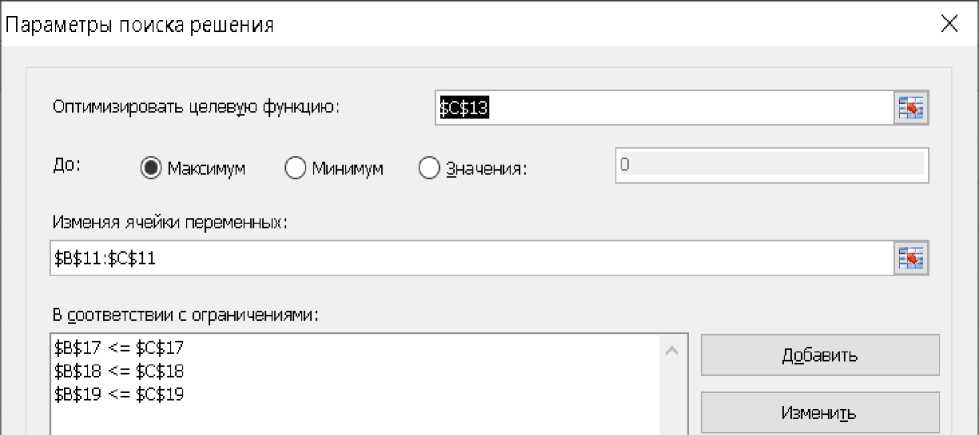
Рисунок 1. Пример заполнения окна поискового решения.

Учет граничных условий в разделе Ограничения осуществляется следующим образом. Когда выбран раздел «Добавить», в результирующее окно вводятся диапазоны, указанные в образце, которые указывают, что количество искомого сырья (В17: В19) не превышает количество сырья на складе (С17: С19).

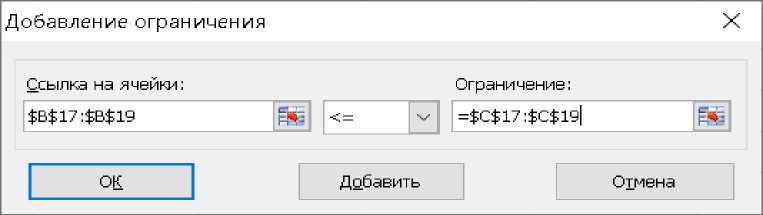
Рисунок 2. Окно ввода граничного условия.

Все граничные условия в модели случая вводятся в указанном выше порядке. Границы в следующих строках указывают на то, что количества продукта (В11: С11) являются ценными и неотрицательными.

После того, как все параметры заданы, выбирается раздел «Найти решение». Результатом является диалоговое окно «Результаты поиска».

Выберите меню «Сохранить» и нажмите «ОК».

Найденное решение является наиболее оптимальным решением для швейной фабрики. Согласно оптимальному плану выпуска, от первого товара - 6, от второго товара - 1. В результате производства этой продукции фабрика заработает 65 000 сумов.

До недавнего времени пользователь должен был знать не только математику, но и работать на компьютере, знать хотя бы один язык программирования и осваивать сложные вычислительные методы для решения своей математической задачи. Для тех, кто не знает программирования, есть готовые научные программного обеспечения, электронные руководства и пакеты прикладных программ (ППП), которые предназначены для выполнения типичных расчетов.

Итак, давайте посмотрим на процесс решения проблемы линейного программирования выше с использованием Mathcad.

В Mathcad функции максимизации и минимизации можно использовать для решения задачи линейного программирования. Эти функции обычно записываются следующим образом:

Maximize (F,<список переменных >)

Minimize (F,< список переменных >)

Решение проблемы линейного программирования в Mathcad выполняется в следующие шаги (рисунок 3):

• 1.    После запуска Mathcad записывается целевая функция, f(х,у)=<представление функции> и вводится начальное значение переменной.

• 2.    Пишется ключевое слово Ginen.

• 3.    Вводятся системы неравенств и ограничений.

• 4. Передаются переменные максимизации или минимизации в

• 5.  Пишется эта переменная и вводится равенство. Результат

• 6.    Чтобы вычислить значение целевой функции, например, напишите функция f (Р 0 , Р 1 ) и введите знак равенства.

функцию.

генерируется в виде вектора.

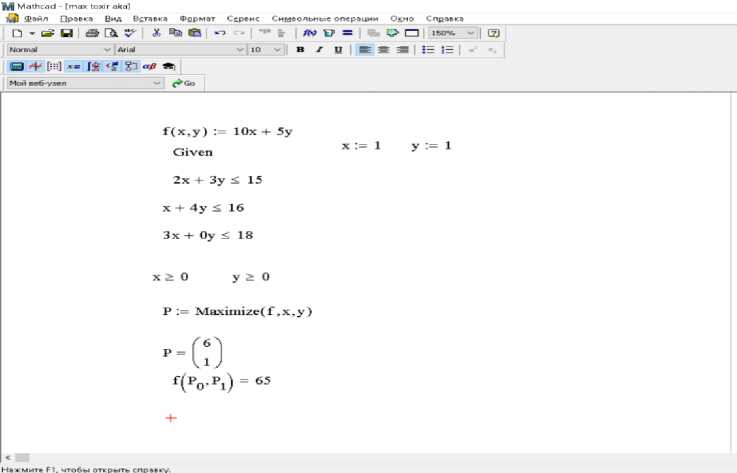
Рисунок 3. Процесс решения задачи линейного программирования в MathCad.

Одним словом, сегодня различные современные технологии программирования используются для решения экономических задач. Все они могут позволить достичь требуемых результатов разными способами. Однако эксперт выбирает один из них в зависимости от содержания проблемы и требований к форме, в которой будут получены результаты. Приведенные выше результаты показывают, что оба метода одинаково эффективны и могут применяться ко всем типам задач линейного программирования.