Использование суперэллипсов в компьютерном моделировании строительных и машиностроительных объектов
Автор: Страшнов С.В.
Рубрика: Инженерная геометрия и компьютерная графика. Цифровая поддержка жизненного цикла изделий
Статья в выпуске: 4 т.23, 2023 года.
Бесплатный доступ
В данной обзорной статье собраны основные сведения по существующим методикам формирования внешних обводов надводных судов, подводных аппаратов и предлагаются новые формы строительных оболочек в виде поверхностей с главным каркасом их трех суперэллипсов. Наличие девяти произвольных констант в обобщенных параметрических уравнениях предлагаемых поверхностей дает возможность, имея один комплект уравнений, рассматривать десятки изучаемых поверхностей с помощью компьютерного моделирования. Даны результаты геометрических исследований и показаны возможности использования расчетной компьютерной программы СКАД в определении напряженно-деформированного состояния строительных оболочек со ссылкой на использованные источники, что может дать толчок дальнейшим исследованиям без повторения уже выполненных другими исследователями. Некоторые разработки проиллюстрированы рисунками, что облегчает понимание материала.
Компьютерное моделирование, суперэллипс, суперэллипсоид, квазиэллипсоид, судостроение, тонкая оболочка, поверхность с тремя направляющими суперэллипсами
Короткий адрес: https://sciup.org/147242671
IDR: 147242671 | УДК: 004.92 | DOI: 10.14529/build230408
Текст научной статьи Использование суперэллипсов в компьютерном моделировании строительных и машиностроительных объектов
Задачей геометров яв ляет с я н е т о льк о р еш е ни е ч и с т о г ео мет ри ч ес ки х з ад ач и п р о блем, н о и п о л уч ени е н овых г ео мет ри ч ес ких ф о р м и мет о дик их п о ст р о е ни я дл я р еш ения п рак ти ч е ских зад ач в р а зл и ч ны х о т р ас л я х н а уки , т е х н ики и с т р о ит е ль с т в а. Со глас н о со вр еме нн ы м т р еб о ва ни я м все в н о вь п р едложе н ны е г ео ме т р ич ес ки е п о с т р о ени я и мет од ики д ол ж н ы б ыт ь р еа л и зованы на ЭВ М , п о э т о м у п р икла д н а я г ео ме т ри я и мее т б о льш о е з н ач е н ие.
Ц е л ью с татьи явл яетс я с бо р ос нов ных м а т ер и а л ов по испол ьз ов а н ию супе рэ лл и п сов в компьютер н ом м оде л ирован ии строи те л ьн ых и машинос троител ь н ых об ъ ек тов п рим е ни те л ь но к м од ел иров а н ию в не ш н их об в одов на д в одны х су дов , подв од ных аппа ра тов и ст роите л ьн ы х об ол очек. П ривед е н ные м а те риал ы и с с л е дов ани й и с п ис ок ис пол ьзов ан ной лите рат у ры по те м е с та тьи м ож е т помочь сокращению сроков ра з ра ботки кон кретных п роект ов и да ть с в ед е ни я д л я да л ь не йш и х исследований.
Общие сведения о суперэллипсахи поверхностях, содержащих суперэллипсы
Суперэллипс – это замкнутая кривая, задаваемая в декартовой системе координат неявным уравнением r x — +
a
y
b
= 1.
С у п ерэл ли пс м ож но з ада ть па ра м е триче с к им и уравнениями:
x = x ( t ) = a c o s2 / r t , y = y ( t ) = b si n 2 / r t . (2)
Суперэллипсы с a = b на зы в а ют кривыми Ламе , или овалами Ламе ( ри с. 1). Су пе рэлл и пс с r = 2/3 при a = b называют а с троидой ; с r = 2 при a * b - эллипсом ; с r = 2 при a = b - окружностью ; с r = 5/2 – с у пе рэ ллипс ом Пита Х е йн а (Piet Hein’s super-ellipse [ 1]). Че м бол ьше з на чен ие п араметра r , т ем точне е фор м а супе рэлл и пс а пр иближ а ется к прям о угол ь ном у кон тур у .
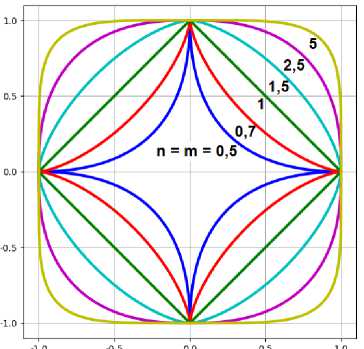
Рис. 1. Кривые Ламе при различных значениях параметра n = m = 0,5; 0,7; 1; 1,5; 2,5; 5
Имеются три группы квазиэллипсоидных поверхностей ( квазиэллипсоидов ). Это – квазиэллип-соидные поверхности с тремя значениями полуосей, квазиэллипсоидные поверхности с шестью значениями полуосей и квазиэллипсоидные поверхности с цилиндрическими вставками [2].
Квазиэллипсоидные поверхности с тремя значениями полуосей задаются уравнением:
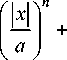
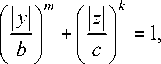
где n , m , k – положительные числа.
При четных значениях показателей степеней n, m, k квазиэллипсоид имеет гладкую поверхность. При показателях степени, стремящихся к бесконечности, поверхность квазиэллипсоида стремится к поверхности прямоугольного параллелепипеда. Квазиэллипсоидная поверхность при n = m = k называется суперэллипсоидом . Координатные линии суперэллипсоидов представляют собой суперэллипсы.
Суперэллипсы можно использовать в качестве направляющих кривых главного каркаса поверхности (рис. 2). Причем три суперэллипса должны лежать во взаимно перпендикулярных координатных плоскостях. В работах [3, 4] предполагается, что плоские кривые главного каркаса рассматриваемых поверхностей заданы в виде:
первая кривая главного каркаса в плоскости xOy (кривая z = 0):
|уГ = ^г(1-^),(4)
вторая кривая главного каркаса в плоскости yOz (кривая x = 0):
IZI" = T"(1-^),(5)
третья кривая главного каркаса в плоскости xOz (кривая y = 0):
|Z|S = 7S (1-1^),(6)
где для выпуклых кривых r, t, n, m, s, k > 1; для вогнутых кривых r, t, n, m, s, k < 1. Кривые (4)–(6) представляют собою суперэллипсы. В формулах (4)–(6) необходимо принимать r = t, n = m, s = k.
Используя методику, изложенную в работах [3, 4], можно получить явные уравнения трех алгебраических поверхностей с одним и тем же главным каркасом (4)–(6)
и с образующим семейством однотипных сечений x = const:
|z| = T(1 - lxlk/Lky/s x x [1 - |y/^|m/(1 - Ix/LI1)™/-]1/"; (7)
с образующим семейством однотипных сечений у = const:
|z| = T(1 - lyl™/^™)1/" x x [1 - Ix/Llk/(1 - |y/^|r)k/£]1/S (8)
ватерлиния (кривая 1) x = –L aterline (the 1st curve)
y y = W мидельшпангоут (кривая 2) midship section (the 2nd curve)
z
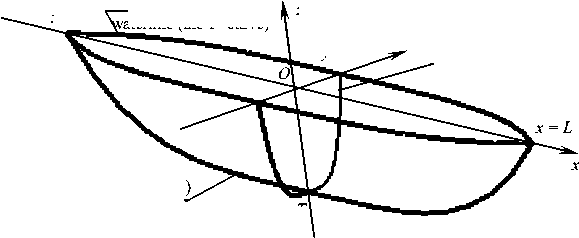
z = –T главный батокс (кривая 3) main buttock (the 3d curve)
Рис. 2. Поверхность с каркасом из трех плоских кривых
и с образующим семейством однотипных се- чений z = const:
|у| = ^(1 - |z|"/T")Vm х х [1 - |x/L|£/(1 - lz/TV;)t/k\-ir, (9)
где –L ≤ x ≤ L, –W ≤ y ≤ W, 0 ≤ z ≤ T.
Явные уравнения поверхностей (7)–(9) можно перевести в параметрическую форму задания: x = x(u) = ±uL, y = y(u,v) = vW[1 – ut]1/r, z = z(u,v) = T[1 – uk]1/s[1 – |v|m]1/n;
x = x ( u,v ) = vL [1 – ur ]1/ t , y = y ( u ) = ±uW, z = z ( u ) = T [1 – um ]1/ n [1 – | v | k ]1/ s ;
x = x(u,v) = vL[1 – us]1/k, y = y(u,v) = ± W[1 – un]1/m[1 – |v|t]1/r,
z = z(u) = uT, где 0 ≤ u ≤ 1, –1 ≤ v ≤ 1; u, v – безразмерные пара- метры.
В формулах (4)–(12) показателям степеней можно давать любые значения, в том числе r ≠ t, n ≠ m, s ≠ k. (13)
В этом случае кривые (3)–(5) будут представлять собою алгебраические кривые любого порядка. А две ветви кривых будут зеркальным отображением друг друга. Следовательно, на координатных линиях будут два симметричных излома кривых.
Обзор исследований по созданию поверхностей с использованием суперэллипсов
В статье [5] впервые было предложено использовать суперэллипсы для создания семейства поверхностей вращения суперэллипса, заданного в параметрической форме (2), вокруг одной из его осей (рис. 3). Составлена компьютерная программа, где в автоматизированном режиме меняется показатель степени в формулах (2).
Методика использования уравнений (10)–(12) при условии (13) изложена в статье [4]. На рис. 4, взятом из [4], построены поверхности с r = 1, t = 2, n = 1, m = 4, s = 1, k = 4.
В этой же статье даны примеры построения поверхностей при условии (13), впервые рассмотренные в работах [6, 7], где для каждой поверхности используется своя методика определения их явных и параметрических уравнений.
Таким образом, в статье [4] впервые показывается, что нет необходимости рассматривать каждую тройку поверхностей с одинаковым главным каркасом, как это делалось в статьях [6–8]. Формулы (7)–(12) описывают весь набор алгебраических поверхностей, задаваемых в явном и параметрическом виде. В работе [9] кривая 2 (см. рис. 2) рассматривается уже как суперэллипс (5), что расширяет возможности компьютерного моделирования. В работе [10] используются формулы (7)–(12) применительно к суперэл- липсам для моделирования замкнутых составных поверхностей вращения с цилиндрической вставкой (рис. 5).
Наличие параметрических уравнений (10)– (12) позволяет смоделировать огромное количество криволинейных геометрических форм.
Из рис. 1 видно, что если взять r = t = 1, или n = m = 1, или s = k = 1, то соответствующие суперэллипсы (4)–(6) вырождаются в ромбы.
Уравнения (10)–(12) были использованы в статье [11] для построения пяти троек новых линейчатых поверхностей. Приведем пример, предложенный в статье [11]. Пусть суперэллипс (4) вырождается в ромб, то есть r = t = 1, суперэллипс (5) вырождается в прямые линии, то есть n = m = 1, а кри- вая (6) остается без изменений, тогда имеем поверхности на плоском ромбическом плане:
x = x ( u ) = ±uL , y = y ( u,v ) = vW [1 – u ] , z = z ( u,v ) = T [1 – uk ]1/ s [1 – | v |] (рис. 6 а );
три
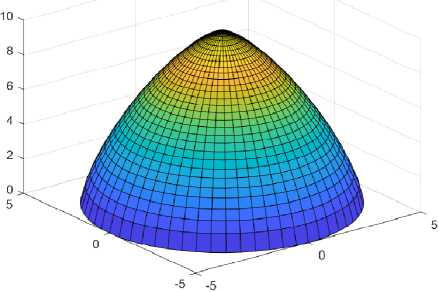
Рис. 3. Поверхность вращения с меридианом в форме суперэллипса (2) с r = 4/3 [5]
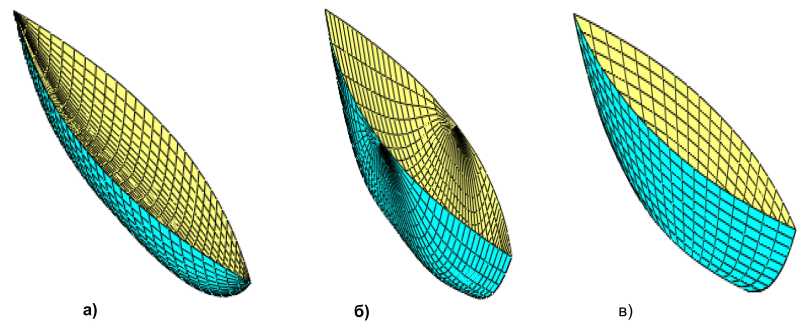
Рис. 4. Поверхности, построенные по формулам: а – (10), б – (11) и в– (12) [4]
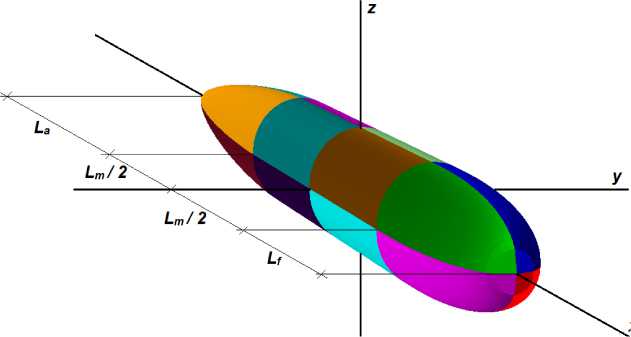
Рис. 5. Поверхность вращения из 4 фрагментов с цилиндрической вставкой и суперэллипсами в плоскостях xOy и zOx [10]
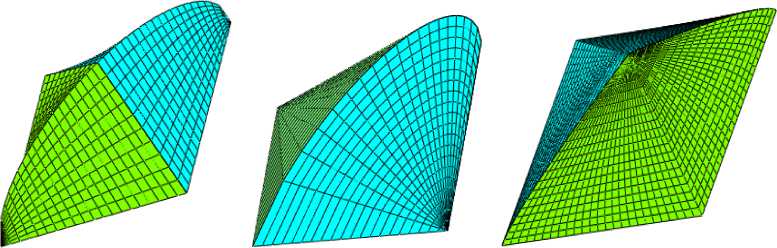
а) б) в)
Рис. 6. Случай 3: Поверхности на плоском ромбическом плане [11]
x = x(u,v) = vL[1 – u], y = y(u) = ±uW, z = z(u) = T[1 – u][1 – |v|k]1/s (рис. 6б);
x = x(u,v) = vL[1 – us]1/k, y = y(u,v) = ± W[1 – u][1 – |v|], z = z(u) = uT (рис. 6в).
На рис. 6 а, б, в показаны три поверхности с s = k = 2 и с одинаковым главным каркасом из суперэллипсов. Очевидно, что поверхности (14) и (16) являются цилиндроидами.
Уравнения (10)–(12) были использованы также в статье [12] для построения четырех троек новых поверхностей, содержащих суперэллипсы, причем один из них вырождается в окружность. В этой статье принято, что суперэллипс (5) представляет собой полуокружность, тогда n = m = 2 и T = W, z ≥ 0. (17)
При таком предположении можно получить четыре группы поверхностей, содержащих полуокружность (17). В каждой группе будет три поверхности с одинаковым главным каркасом. Пусть суперэллипс (6) вырождается в ромб, тогда s = k = 1, n = m = 2. На рис. 7, взятом из статьи [12], представлена тройка поверхностей с одинаковым главным
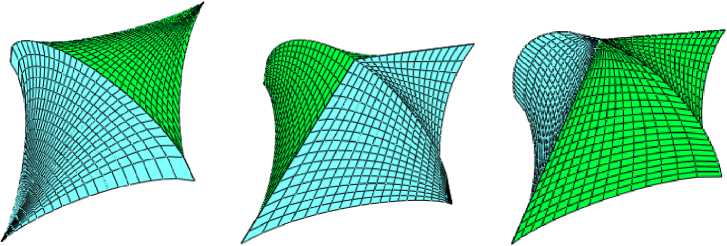
а) б) в)
Рис. 7. Аналитические поверхности с окружностью в плоскости yOz:
а) поверхность построена по формулам (10); б) поверхность построена по формулам (11);
в) поверхность построена по формулам (12)
каркасом при габаритных размерах T = W = 5 м, L = 7 м и при r = t = 3/4.
Поверхности диагонального переноса образуются по принципу переноса плоской кривой по направляющей так, что при скольжении образующей кривой по плоскому неподвижному контуру две ее симметричные точки непрерывно его касаются.
Велароидальной называется поверхность переноса на плоском прямоугольном плане с образующей кривой переменной кривизны. Таким образом, поверхность ограничена четырьмя взаимно ортогональными контурными прямыми, лежащими в одной плоскости [13].
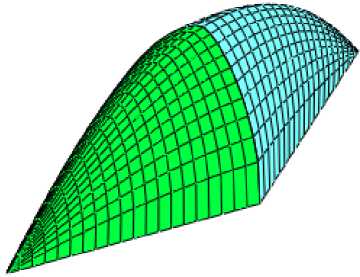
В работе [14] предлагаются для внедрения поверхности диагонального переноса велароидаль-ного типа на ромбическом плане, для построения которых также используются параметрические уравнения (10)–(12). В статье [14] рассмотрено несколько примеров поверхностей, содержащих один вырожденный суперэллипс, т. е. r = t = 1, и хотя бы один суперэллипс (5) с m = n = 1,5 и s = 1, k = 2. Тогда параметрические уравнения (10) будут:
x = x(u) = ±uL, y = y(u,v) = vW[1 – u], z = z(u,v) = T[1 – u2][1 – |v|1,5]2/3 , где 0 ≤ u ≤ 1 (рис. 8а) и –1 ≤ u ≤ 1 (рис. 8б), –1 ≤ v ≤ 1; u, v – безразмерные параметры.
Суперэллипсы в судостроении
Как отмечается в работе [7], «выбор формы корпуса обусловлен многими факторами: назначение судна, очертание ватерлинии, сопротивление воды, трудоемкость изготовления, разделение на конструктивные модули, скорость движения судна, архитектурные требования и др.». Эти факторы влияют на выбор плоских кривых основного каркаса (см. рис. 2). Наличие формул (4)–(12) позволит облегчить выбор поверхности судового корпуса, используя аналитические зависимости, что может снизить первоначальные затраты на начальных этапах проектирования. Имея аналитические поверхности, рекомендуемые для формовки внешнего судового корпуса из тонкого листа на первом этапе проектирования, можно решать вопросы сборки корпуса [15], проблемы прочности [16], оптимизации корпуса [17, 18], сопротивления воды [19] и т. д.
Есть работы [10, 19–21], обосновывающие возможности применения поверхностей с главным каркасом из суперэллипсов и цилиндрической вставкой для формирования внешних обводов подводных аппаратов и подводных лодок (см. рис. 5). В процессе эволюции подводных лодок выработался определенный стереотип их внешнего облика. Считается, что характерным для
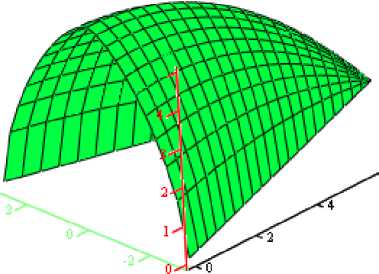
Рис. 8. Поверхность переноса на ромбическом плане с образующим суперэллипсом и направляющей параболой в плоскости xOz [14]
б)
не го я в л яетс я б лиз ка я к кр у гов ой форм а попе речных с е чени й на р у ж ного ко рп ус а пра кт иче с к и на всей его длине, полуэл лип тиче с ка я в п л а не и на в иде с бо к у н осовая окон еч н ос ть, бл изка я к кон у су кормов а я оконе чнос ть [22]. В с ре дне й по длин е ч а с ти корп у с а им е е тс я ци л и ндриче ска я в ста в ка , протяженность которой со ста в л яет 10 –40 % от длины под в од ной л од ки. Эти ге ом е триче с ки е пар а м е тры м ож но обе с пе чит ь, ра з бив ге ом е трич еск ую м оде л ь корп ус а по дв одного аппа ра та на шесть фрагментов ( р и с . 9). Д а л е е геометрическая мод ел ь с трои тс я с пом ощью формул (4)–(12). Эту мод ел ь м ож но в з я ть з а основу на пе рв ом эта пе проектирования.
Суперэллипсы в моделировании строительных оболочек
Геометрические модели, представленные на рис. 3, 6–8, могут быть применены в архитектуре и строительстве тонких оболочек. В работе [23] была найдена оптимальная по прочности тонкая оболочка из четырех рассмотренных, срединные поверхности которых представляют собой разные поверхности с главным каркасом из трех суперэллипсов. Для сравнения были взяты четыре оболочки с одинаковыми габаритными размерами 2L, 2W, T, срединные поверхности которых задаются с помощью формул (12). Срединные поверхности четырех оболочек отличаются только степенными показателями s = k, n = m, r = t. Система криволинейных координатных линий u, v является не орто- гональной, за исключением пересечения опорной линии u = 0 с координатными линиями u. Для получения параметров напряженно-деформированного состояния в вычислительном комплексе SCAD создана конечно-элементная расчетная схема для трех оболочек, собранная из четырех моделей-схем исследуемой поверхности с различными сетками плоских конечных элементов. Расчет на действие собственного веса показал малое различие в результатах.
Напряженно-деформированное состояние тонких оболочек со срединными поверхностями, которые содержат заданные суперэллипсы в трех координатных плоскостях
Имеется работа [24], где определяется напряженно-деформированное состояние тройки линейчатых оболочек (рис. 10), предложенных для внедрения в статье [11]. Из представленных в статье изополей очевидно, что напряженно-деформированные состояния разных линейчатых оболочек на овальном плане, но с одним и тем же главным каркасом, отличаются незначительно у двух из трех оболочек. При этом было установлено, что данные две оболочки имеют отрицательную гауссову кривизну, а третья – нулевую. Следовательно, отмечают авторы работы [24], искать оптимальную оболочку по критерию прочности среди двух оболочек с отрицательной гауссовой кривизной не имеет смысла, следует выбирать оболочку по
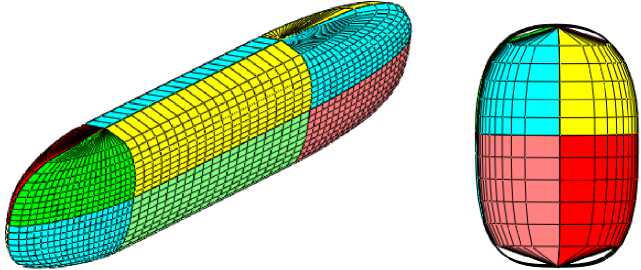
Рис. 9. Геометрическая модель подводного аппарата из шести фрагментов, каждый из которых задается формулами (9): общий вид и поперечное сечение
а) б) в)
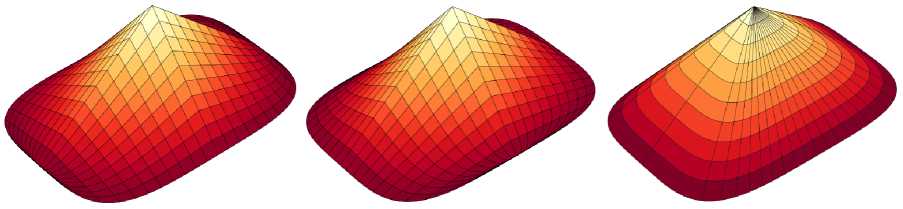
Рис. 10. Линейчатые поверхности на плоском овальном плане: a) поверхность, заданная уравнениями (10); б) поверхность, заданная уравнениями (11); в) поверхность, заданная уравнениями (12)
а)
б)
в)
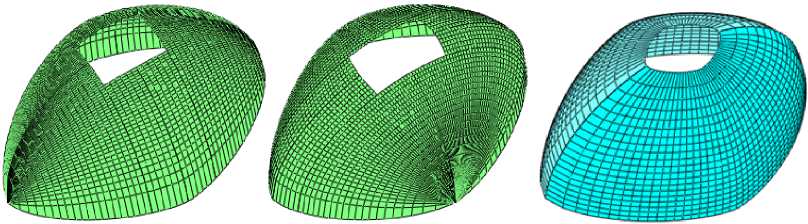
Рис. 11. Поверхности, описываемые параметрическими уравнениями (10)–(12), L = 10 м, W = 7 м, T = 10 м, s = k = 2 , n = m = 2, r = t = 1,5: а ) поверхность построена по формулам (10); б ) поверхность построена по формулам (11); в ) поверхность построена по формулам (12)
другому критерию, например, по критерию трудоемкости изготовления.
Третья попытка предложить архитекторам тройку оболочек с одинаковыми габаритными размерами, срединные поверхности которых задаются с помощью формул (10)–(12), была предпринята в статье [25]. Были рассмотрены оболочки со срединными поверхностями, описываемыми параметрическими уравнениями (10)–(12). Исследование оболочек (рис. 11) в статье [25] выполнено с помощью программы SCAD на базе метода конечных элементов. Анализ полученных результатов напряженного состояния трех исследуемых оболочек показывает, что в них при действии нагрузки типа собственного веса возникают как сжимающие, так и растягивающие напряжения.
Зарубежные исследования напряженно-деформированного состояния тонких оболочек с главным каркасом из трех суперэллипсов представлены только одной работой [17], где изучается потеря устойчивости оболочки, заданной в виде (3) при n = m = k – четные числа, от действия равномерного внешнего давления.
Результаты исследования
Как показали исследования, выполненные группой ученых Инженерной академии Российского университета дружбы народов им. П. Лумумбы [3–7, 9–14, 22–25] криволинейные поверхности с главным каркасом из трех суперэллипсов могут найти применение как в строительстве обо- лочечных структур и тонких оболочек, так и в судостроении. В области судостроения ими впервые предложены обобщенные уравнения поверхностей для формирования внешнего корпуса судов и подводных аппаратов. До них методика формирования внешних обводов разрабатывалась отдельно для каждого случая на основании экспериментальных данных или исходя из опыта проектировщиков. Естественно, предложенная методика формирования внешнего корпуса судов и подводных аппаратов может быть использована только на первом этапе проектирования. Далее потребуются уточнения и корректировки.
Новые формы строительных оболочек предложены впервые. Показана возможность их расчета на прочность при помощи существующих компьютерных программ.
В данной обзорной статье собраны воедино все материалы по заявленной теме с указанием использованной литературы, что значительно упростит дальнейшую работу заинтересовавшихся исследователей.
Заключение
Все представленные методики по формированию внешних обводов надводных кораблей, подводных аппаратов и строительных оболочек, разработанные исследователями из РУДН, легко реализуются на ЭВМ, что дает возможность использовать многовариантное проектирование и выбирать оптимальное изделие по выбранному критерию.
Список литературы Использование суперэллипсов в компьютерном моделировании строительных и машиностроительных объектов
- Gardner M. Mathematical Carnival. A New Round-Up of Tantalizers and Puzzles from Scientific American. New York: Vintage Press, 1977. P. 240–254.
- Никитюк В.А. Квазиэллипсоидные поверхности // Архитектура оболочек и прочностной расчет тонкостенных строительных и машиностроительных конструкций сложной формы: Труды Международной научной конференции, Москва, 4–8 июня 2001. М.: Изд-во РУДН, 2001. С. 315–318.
- Krivoshapko S.N. Tangential developable and hydrodynamic surfaces for early stage of ship shape design // Ships and Offshore Structures. 2022. No. 18(3). P. 1–9. DOI: 10.1080/17445302.2022.2062165
- Кривошапко С.Н. Алгебраические судовые поверхности с каркасом из трех плоских кривых в координатных плоскостях // Вестник Российского университета дружбы народов. Серия: Инженерные исследования. 2022. Т. 23, № 3. С. 207–212. DOI: 10.22363/2312-8143-2022-23-3-207-212
- Страшнов С.В. Компьютерное моделирование новых форм строительных оболочек // Геометрия и графика. 2022. № 4. С. 26–34. DOI: 10.12737/2308-4898-2022-10-4-26-34
- Кривошапко С.Н. Гидродинамические поверхности // Судостроение. 2021. № 3(856). С. 64–66. DOI: 10.54068/00394580_2021_3_64
- Кривошапко С.Н., Иванов В.Н. Алгебраические поверхности для рациональных судовых корпусов // Технология машиностроения. 2022. № 3. С. 17–24.
- Авдоньев Е.Я. Аналитическое описание корпусных поверхностей // Прикладная геометрия и инженерная графика. 1972. Вып. 15. С. 156–160.
- Карневич В.В. Гидродинамические поверхности с мидель-шпангоутом в форме кривых Ламе // Вестник Российского университета дружбы народов. Серия: Инженерные исследования. 2021. Т. 22, № 4. С. 323–328. DOI: 10.22363/2312-8143-2021-22-4-323-328
- Карневич В.В. Построение гидродинамических поверхностей каркасами из кривых Ламе на примере корпуса подводной лодки // Вестник Российского университета дружбы народов. Серия: Инженерные исследования. 2022. Т. 23, № 1. С. 30–37. DOI: 10.22363/2312-8143-2022-23-1-30-37
- Мамиева И.А. Линейчатые алгебраические поверхности с главным каркасом из трех суперэллипсов// Строительная механика инженерных конструкций и сооружений. 2022. Т. 18, № 4. С. 387–395. DOI: 10.22363/1815-5235-2022-18-4-387-395.
- Krivoshapko S.N. Surfaces with a main framework of three given curves which include one circle // Structural Mechanics of Engineering Constructions and Buildings. 2023. Vol. 19(2). P. 210–219. DOI: 10.22363/1815-5235-2023-19-2-210-219
- Страшнов С.В. Велароидальные оболочки и оболочки велароидального типа // Геометрия и графика. 2022. № 2. С. 11–19. DOI: 10.12737/2308-4898-2022-10-2-11-19.
- Кривошапко С.Н. Поверхности диагонального переноса велароидального типа на ромбическом плане // Строительство и реконструкция. 2023. № 2 (106). C. 59–69. DOI: 10.33979/2073-7416-2023-106-2-59-69
- Kwang Hee Ko. A Survey: application of geometric modeling techniques to ship modeling and design // International Journal of Naval Architecture and Ocean Engineering. 2010. Vol. 2, Iss. 4. P. 177–184. DOI: 10.2478/IJNAOE-2013-0034
- Ma Y.Q., Wang C.M., Ang K.K. Buckling of superellipsoidal shells under uniform pressure // Thin- Walled Structures. 2008. Vol. 46(6). P. 584–591 DOI: 10.1016/j.fws.2008.01.013
- Janson C., Larsson L. A method for the optimization of ship hulls from a resistance point of view // National Research Council. 1997. Twenty-First Symposium on Naval Hydrodynamic. Washington. DC: The National Academies Press. Pp. 680–696 DOI: 10.17226/5870
- Concepts in submarine shape design / M. Moonesun, A. Mahdion, Yu.M. Korol et al. // Indian Journal of Geo-Marine Sciences. 2016. No. 45(1). P. 100–104.
- Evaluation of submarine motions under irregular ocean waves by panel method / M. Moonesun, A. Mahdian, O. Korneliuk et al. // Indian Journal of Geo Marine Sciences. 2019. No. 48 (09). P. 1485–1495.
- Budak G., Beji S. Computational resistance analyses of a generic submarine hull form and its geometric variants // The Journal of Ocean Technology. 2016. No. 11(2). P. 77–86.
- Onur Usta. Numerical investigation on the resistance characteristics of nature inspired underwater vehicles // Proceedings of the 2nd International Congress on Ship and Marine Technology / Ed.: Alkan A.D., Ölmez H. and Demirel Y.D., 16–18 September 2021. İstanbul: Yıldız Teknik Üniversitesi; 2021. P. 285–294
- Вакс А.И., Мурадян В.А., Сагайдаков Ф.Р. Подводные лодки. Прошлое, настоящее, будущее. СПб.: ЦНИИ им. акад. А.Н. Крылова, Судостроение, 2001. 125 с.
- Кривошапко С.Н., Алёшина О.О., Иванов В.Н. Статический расчет оболочек, очерченных по поверхностям с главным каркасом из трех заданных суперэллипсов // Строительная механика и расчет сооружений. 2022. № 6 (305). С. 18–27. DOI: 10.37538/0039-2383.2022.6.18.27
- Мамиева И.А., Карневич В.В. Геометрия и статический расчет тонких оболочек с линейчатыми срединными поверхностями с главным каркасом из трех суперэллипсов // Строительство и реконструкция. 2023. № 1(105). С. 16–27. DOI: 10.33979/2073-7416-2023-105-1-16-27
- Алешина О.О. Геометрия и статический расчёт тонких оболочек в форме поверхности диагонального переноса велароидального типа // Строительная механика инженерных конструкций и сооружений. 2023. Т. 19, № 1. С. 84–93. DOI: 10.22363/1815-5235-2023-19-1-84-93


